论文翻译：HetConv-Heterogeneous Kernel-Based Convolutions for Deep CNNs

Abstract

我们提出了一种新颖的深度学习架构，其中卷积操作利用了异构内核。与标准卷积运算相比，所提出的HetConv（基于异构内核的卷积）减少了计算（FLOPs）和参数的数量，同时仍保持表示效率。为了证明我们提出的卷积的有效性，我们在标准卷积神经网络（CNN）架构上提供了广泛的实验结果，如VGG和ResNet。 我们发现在用我们提出的HetConv滤波器替换这些架构中的标准卷积滤波器后，我们实现了基于3X到8X FLOPs的速度提升，同时仍然保持（有时提高）精度。 我们还将我们提出的卷积与组/深度方式的卷积进行比较，并表明它可以以更高的精度实现更多的FLOPs减少。

1. Introduction

卷积神经网络在视觉和NLP等领域表现出了显著的性能。进一步提高性能的总趋势使模型更加复杂和深入。随着网络的深入，通过增加模型复杂度来提高精度并不是免费的；它伴随着计算量(FLOPs)的大幅增加。因此，人们提出了各种卷积运算/卷积滤波器，以减少对模型的FLOPs，提高模型的效率。

现有的卷积滤波器可以粗略地分为三类：1-深度卷积滤波器执行深度卷积（DWC），2-逐点卷积滤波器执行逐点卷积（PWC）和3-组循环卷积滤波器执行 分组卷积（GWC）。 大多数最近的架构使用这些卷积滤波器的组合来使模型有效。使用这些卷积（例如，DWC，PWC和GWC），许多流行的模型已经探索了新的架构来减少FLOPs。但是，设计新架构需要大量工作才能找到最佳的滤波器组合，从而实现最小的FLOPs。

另一种提高模型效率的流行方法是使用模型压缩。模型压缩大致可分为三类:连接剪枝、滤波器剪枝和量化。

在滤波器剪枝中，其思想是剪枝模型中贡献最小的筛选器，在删除此筛选器/连接之后，通常对模型进行微调以保持其性能。在修剪模型时，我们需要一个预先训练的模型(可能需要一个计算上昂贵的训练作为预处理步骤)，然后我们丢弃贡献最小的过滤器。因此，这是一个非常昂贵和棘手的过程。因此，使用有效的卷积滤波器或卷积运算来设计一个有效的架构是比剪枝更流行的方法。这并不需要昂贵的训练，然后修剪，因为训练是从头开始有效地完成。

使用有效的卷积滤波器，有两个不同的目标。一种工作侧重于设计具有最小FLOPs而同时降低精度的架构。这些工作重点是开发物联网/低端设备的模型。这些模型的精度较低，因此必须搜索最佳模型，以在精度和FLOPs之间建立平衡。因此，在FLOP和模型精度之间存在权衡。

另一组工作侧重于提高准确性，同时保持模型FLOPs与原始架构相同。最近的架构，如Inception，RexNetXt和Xception就是这类工作的例子。他们的目标是使用有效的卷积滤波器设计更复杂的模型，同时保持FLOPs与基本模型相同。通常期望更复杂的模型可以学习更好的特征，从而获得更好的准确性。但是，这些方法并不专注于设计新架构，而主要是在标准基础架构中使用现有的高效过滤器。因此，这些工作保持层数和体系结构与基础模型相同，并增加每层上的过滤器，使其不增加FLOPs。

与这两种方法相比，我们工作的主要重点是通过设计新内核来减少给定模型/体系结构的FLOP，而不会影响精度损失。 在实验上我们发现所提出的方法具有比现有技术修剪方法低得多的FLOPs，同时保持基础模型/架构的准确性。修剪方法非常昂贵，并且显示出实现FLOPs压缩的准确性显着下降。

在提出的方法中，我们选择了一种不同的策略来提高现有模型的效率，同时又不牺牲精度。架构搜索需要多年的研究才能得到优化的架构。因此，我们没有设计一个新的高效的架构，而是设计了一个高效的卷积运算(卷积滤波器)，它可以直接插入到任何现有的标准架构中以减少FLOPs。为了实现这一点，我们提出了一种新型的卷积——异构卷积。

卷积运算可以根据核的类型分为两类：

• 使用传统卷积滤波器的同构卷积(例如标准卷积、群卷积、深度卷积、点卷积)。同构卷积可以用同构滤波器来实现。如果一个过滤器包含所有大小相同的内核，那么它就是同构的（例如，在一个\(3\times 3\times 256\) CONV2D过滤器中，所有256个内核的大小都是\(3 \times 3\)）。
• 异构卷积使用异构卷积滤波器(HetConv)。如果一个过滤器包含不同大小的内核，那么它就是异构的(例如，在HetConv过滤器中，256个内核中有一些内核大小为\(3\times 3\)，其余的内核大小为\(1 \times 1\))。

在深度CNN中使用异构滤波器克服了现有基于高效架构搜索和模型压缩的方法的局限性。最新的高效架构之一MobileNet使用深度和点卷积。标准的卷积层被两个卷积层替换，因此它有更多的延迟（延迟1，延迟也可以简单的理解为速度慢于基准模型的多少）。有关延迟的详细信息，请参阅- 3.3节和图4。但是我们提出的HetConv具有与原始架构相同的延迟（延迟为零），而不像具有大于零的延迟。

与高精度下降的模型压缩相比，我们的方法与ResNet和VGGNet等标准模型的最新结果相比具有很强的竞争力。 使用HetConv过滤器，我们可以从头开始训练我们的模型，而不像需要预训练模型的修剪方法，而不会牺牲准确性。 如果我们增加FLOPs修剪的程度，修剪方法也会遭受严重的精确度下降。 使用提出的Het-Conv滤波器，与FLOPs修剪方法相比，我们拥有关于FLOPs的最新结果。 此外，修剪过程效率低，因为修剪后需要花费大量时间进行训练和微调。 我们的方法非常高效，并且在从头开始训练时，与原始模型相比，提供了类似的结果。

据我们所知，这是第一个异构的卷积/过滤器。这种异构设计有助于提高现有架构的效率（FLOPs降低），而不会牺牲精度。 我们在ResNet，VGG-16等不同架构上进行了大量实验，只需将原来的滤波器替换为我们提出的滤波器即可。 我们发现，在不牺牲这些模型的准确性的情况下，我们将FLOPs的高度降低（3倍到8倍）。与现有的修剪方法相比，这些FLOPs减少甚至更好。

我们的主要贡献如下：

• 我们设计了一个高效的异构卷积滤波器，它可以插入到任何现有的架构中，在不牺牲精度的前提下，提高架构的效率(将FLOPs减少3到8倍)。
• 提出的HetConv滤波器的设计方式是零延迟。因此，从输入到输出的延迟可以忽略不计。

2. Related Work

最近深度神经网络的成功取决于模型设计。为了实现最小的错误率，模型变得越来越复杂。 复杂而深入的架构包含数百万个参数，需要数十亿次FLOP（计算）。 这些模型需要具有高端规格的机器，并且这些类型的架构在低计算资源上效率非常低。 这引起了人们对设计高效模型的兴趣。提高模型效率的工作可分为两部分。

2.1. Efficient Convolutional Filter(高效的卷积过滤器)

为了设计高效的卷积滤波器，近年来提出了几种新型的卷积滤波器。其中分组卷积(GWC)、深度卷积(DWC)[38]和点态卷积(PWC)是常用的卷积滤波器。它们被广泛用于设计高效的体系结构。GoogleNet使用inception模块和不规则的堆叠架构。Inception模块使用GWC和PWC来减少FLOPs。ResNet使用瓶颈结构来设计具有剩余连接的高效架构。它们使用PWC和标准卷积，有助于在不增加模型参数的情况下更深入，并减少FLOP爆炸。因此，与VGG相比，他们可以设计更深入的架构。ResNetxt使用ResNet架构，他们用GWC和PWC划分每一层。因此，在不增加FLOP的情况下，它们可以增加基数1.它们表明增加基数比更深或更宽的网络更有效。SENet设计了一种新的连接，它为每个输出特征映射赋予了权重，虽然FLOPs略有增加，但性能却有所提升。

MobileNet是另一种流行的架构，专为包含DWC和PWC的物联网设备而设计。这种架构在FLOP方面非常轻便且高效。FLOP的减少不是免费的，并且与最先进的模型相比，精度下降的成本也随之降低。在同一层使用不同类型的卷积滤波器，但由于每个过滤器中存在相同类型的内核，所以每个滤波器执行的卷积都是同构的。在相同层使用不同类型的卷积滤波器也有助于减少参数FLOP。在我们提出的卷积中，由于每个滤波器中存在不同类型的内核，卷积操作是异构的。

2.2. Model Compression（模型的压缩）

另一种提高CNN效率的流行方法是模型压缩。这些可以分为:1-连接剪枝，2-过滤器剪枝和3位压缩。与其他方法相比，滤波器剪枝方法更有效，并且在FLOPs方面具有较高的压缩率。此外，过滤器修剪方法不需要任何特殊的硬件/软件支持(稀疏库)。

在滤波器剪枝中，大部分工作都是根据一定的准则计算滤波器的重要性，然后对其进行剪枝，然后进行再训练以恢复精度下降。使用L1范数作为排名过滤器的度量。但是，剪枝是在预先训练的模型上完成的，包括迭代训练和剪枝，这是昂贵的。此外，如果触发器剪枝的程度增加，则滤波器剪枝的精度会急剧下降。

3. Proposed Method（提出的方法）

在这项工作中，我们提出了一种新颖的滤波器/卷积（Het-Conv），它包含异构内核（例如，少数内核的大小为\(3 \times 3\)，其他内核可能为\(1 \times 1\)），以减少现有模型的FLOPs。 与原始模型的精度相同。这与由均匀内核（例如全部\(3 \times 3\)或全部\(5 \times 5\)）组成的标准卷积滤波器非常不同。异构滤波器在FLOPs方面非常有效。它可以近似为分组卷积滤波器（GWC）和逐点卷积滤波器（PWC）的组合滤波器。为了减少卷积层的FLOPs，我们通常将其替换为两层或更多层（GWC / DWC和PWC），但它会增加延迟，因为下一层的输入是前一层的输出。因此，必须按顺序完成所有计算以获得正确的输出。相比之下，我们提出的HetConv具有相同的延迟。标准滤波器和HetConv滤波器之间的差异如图1和图2所示。

图1 标准卷积过滤器（同构）和异构卷积过滤器（HetConv）之间的诧异。其中M是指输入深度（输入通道的数量），P是指part（控制卷积过滤器中不同类型的核的数量）。在M个核中，\(\frac MP\)核的大小是\(3×3\)，其余的都是\(1×1\)。

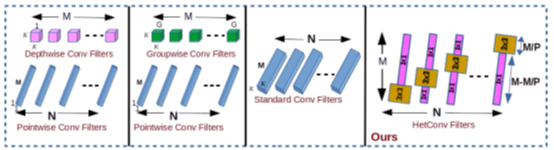
图2 将所提出的卷积滤波器(HetConv)与其他有效卷积滤波器进行比较。我们的异构过滤器的延迟为零，而其他过滤器(GWC+PWC或DWC+PWC)的延迟为一个单元。

在标准卷积层中，假设输入(输入特征图)的大小为\(D_i\times D_i\times M\)。其中\(D_i\)为输入的正方形特征图空间宽度和高度，\(M\)为输入深度(输入通道数)。还要考虑\(D_o\times D_o\times N\)是输出特性映射。这里\(D_o\)是输出的正方形特征图空间宽度和高度，\(N\)是输出深度(输出通道数)。应用\(K\times K\times M\)大小的N个滤波器得到输出特征图。这里K是内核大小。因此，这一\(L\)层的总计算成本为：

\[FL_S=D_o\times D_o \times M \times N \times K \times K \tag{1} \]

由式(1)可以看出，计算代价与核大小(K)、feature map大小、输入通道M和输出通道n有关。这种计算代价非常高，可以通过精心设计新的卷积运算进一步降低。为了减少高计算量，提出了各种卷积，如DWC、PWC和GWC，这些卷积在许多最近的架构中被使用来减少FLOPs，但它们都增加了延迟。

标准卷积运算和一些最近的卷积运算使用同构核(即，对于整个过滤器，每个内核的大小相同)。为了提高效率，我们使用了异构内核。对于同一个过滤器，它包含不同大小的内核。请参考图3来可视化特定层l上的所有过滤器。我们定义P部分，它控制卷积过滤器中不同类型内核的数量。对于第P部分，总内核中的\(\frac{1}{P}\)部分为\(K\times K\)大小，其余部分\((1-\frac1P)\)为\(1\times 1\)大小。为了更好地理解，让我们举个例子，在一个\(3\times3\times 256\)标准CONV2D过滤器中，如果您将\((1-\frac1P)\times 256\)、\(3\times 3\)个内核替换为\(1\times 1\)(沿着中轴)，您将得到一个带有\(P\)部分的HetConv过滤器。请参见图1和图2。

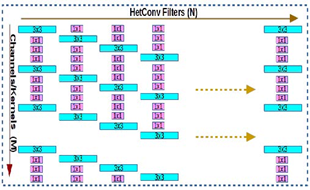
图3 第\(L\)层卷积滤波器：使用异构内核的卷积滤波器(HetConv)。在图中，每个通道由大小为\(3 \times 3\)和\(1\times 1\)的异构内核组成。在标准卷积滤波器中，用\(1\times 1\)的核替换\(3 \times 3\)的核，在保持精度的同时，大大减少了误操作。特定层的过滤器以移位的方式排列(即，如果第一个过滤器从第一个位置启动\(3\times 3\)内核，那么第二个过滤器从第二个位置启动\(3 \times 3\)内核，以此类推)。

在层\(L\)上有\(P\)部分的Hetconv滤波器中，\(k\times k\)大小的核的计算成本如下所示：

\[FL_K=\frac{(D_o \times D_o \times M \times N \times K \times K)}{P} \tag{2} \]

它降低了P倍的成本，因为我们现在只有\(\frac MP\)个\(K \times K\)大小的核。

其余的\((M-\frac MP)\)内核大小为\(1\times 1\)。剩余的\(1\times 1\)个内核的计算成本为：

\[FL_1 = (D_o \times D_o \times N) \times (M - \frac MP) \tag{3} \]

因此，第\(L\)层的总计算成本为：

\[FL_{HC} = FL_K + FL_1 \tag{4} \]

与标准卷积相比，计算的总减少量（R）可表示为：

\[R_{HetConv} = \frac {FL_K + FL_1}{FL_S} =\frac1P + \frac{1-\frac1P}{K^2} \tag{5} \]

在方程5中，如果我们令\(P = 1\)，那么它就变成了标准卷积滤波器。

通过将某些通道上的过滤器大小从\(3\times 3\)减小到\(1 \times 1\)，我们正在减小过滤器的空间范围。但是，通过在某些信道上保持\(3\times 3\)的大小，我们可以确保滤波器覆盖了某些信道上的空间相关性，并且不需要在所有信道上都具有相同的空间相关性。我们在实验部分观察到，通过这样做，我们可以获得与同构过滤器相似的精度。另一方面，如果我们避免并保留所有通道上的\(1\times1\)滤波器大小，那么我们就不会覆盖必要的空间相关信息，并且精度会受到影响。

3.1. Comparision with DepthWise followed by PointWise Convolution（比较深度卷积和点卷积）

在极端情况下，HetConv中\(P=M\)时，HetConv可以与DWC+PWC(深度卷积后点卷积)进行比较。MobileNet使用这种类型的卷积。虽然MobileNet比我们的极端情况有更多的FLOPs与更多的延迟，因为MobileNet有一个延迟。

对于第\(L\)层，DWC+PWC (MobileNet)的总FLOPs数可以计算为：

\[FL_{MobNet} =D_o \times D_o \times M \times K \times K + M \times N \times D_o \times D_o \tag{6} \]

因此总的计算量比标准卷积减少了：

\[R_{MobNet}=\frac{FL_{MobNet}}{FL_S}=\frac 1N + \frac{1}{K^2} \tag{7} \]

从公式5可以清楚地看出，我们可以改变\(P\)部分的值来在精度和FLOPs之间进行权衡。 如果我们减小\(P\)值，产生的卷积将更接近标准卷积。 为了显示所提出的HetConv滤波器的有效性，我们在实验部分中显示了结果，其中HetConv使用类似的FLOP实现了明显更好的精度。

在\(P = M\)的极端情况下，由公式5和7(对于MobileNet \(N = M\))，我们可以得出结论：

\[\frac 1M + \frac{(1-\frac1M)}{K^2}< \frac 1M + \frac{1}{K^2} \tag{8} \]

与标准卷积相比计算量的总减少：

\[Speedup = \frac{1}{Reduction} \tag{9} \]

因此，从公式8可以看出，MobileNet比我们的方法需要更多的计算。在我们的HetConv中，延迟为零，而MobileNet的延迟为1。在这种极端情况下，我们的精度明显高于MobileNet(请参阅实验部分)。

3.2. Comparision with GroupWise followed by PointWise Convolution（与GroupWise比较，然后是PointWise Convolution）

对于组大小为\(G\)的群向卷积和点态卷积(GWC+PWC)，第\(L\)层的GWC+PWC总的FLOPs次数可以计算为：

\[FL_G = \frac{(D_o \times D_o \times M \times N \times K \times K)}{G+ M \times N \times D_o \times D_o} \tag{10} \]

因此计算的总减少与标准的卷积比较：

\[R_{Group} = \frac {FL_G}{FL_S} = \frac1G + \frac{1}{K^2} \tag{11} \]

同样的，当\(P=G\)时，由公式5和11得到：

\[\frac 1P + \frac{(1-\frac1P)}{K^2}<\frac1P + \frac{1}{K^2} \tag{12} \]

因此，从公式12可以看出，GWC+PWC的计算量明显大于我们的方法。在HetConv中，我们的延迟为零，而GWC+PWC的延迟为1。

3.3. Running Latency（运行延迟）

大多数先前的方法设计了有效的卷积来减少FLOP，但它们增加了架构中的延迟。 不同类型卷积的延迟如图4所示。 在Inception模块中，一层被分解为两个或更多个连续层。因此，体系结构中的延迟大于零。 在Xception中应用第一个GWC，并且在GWC的输出上应用PWC。 PWC等待GWC的完成。 因此，这种方法减少了FLOP，但增加了系统的延迟。 类似地，在MobileNet中，第一个DWC然后应用PWC，因此它具有延迟1。 此延迟包括GPU等并行设备的延迟。在我们提出的方法中，任何层都不会被连续层替换，因此延迟为零。我们直接设计过滤器，这样可以在不增加任何延迟的情况下减少FLOP。 与先前的有效卷积相比，我们提出的方法在FLOP方面非常有竞争力，同时保持延迟为零。

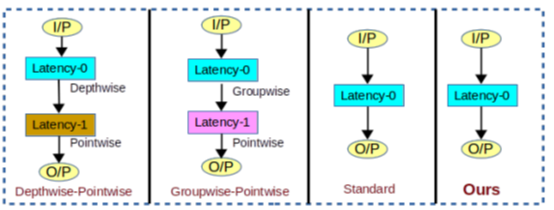
图4 图中显示了不同类型卷积在延迟方面的比较。

3.4. Speedup over standard convolution for different values of P（对于不同的P值，加速标准卷积）

如图-5所示，加速比随P值增加。我们可以使用P值在准确度和FLOP之间进行权衡。 如果我们减小P值，产生的卷积将更接近标准卷积。 为了显示所提出的HetConv滤波器的有效性，我们在实验部分中显示了结果，其中Het-Conv相对于具有类似FLOPs的其他类型的卷积实现了显着更好的准确性。

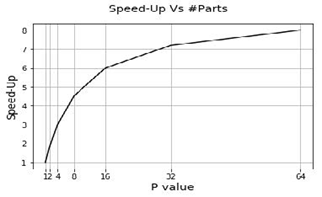
图5 对于具有\(3 \times 3\)和\(1 \times 1\)内核的HetConv滤波器，针对不同\(P\)值的标准卷积加速。

4. Experiments and Results（实验和结果）

为了证明所提出的Hetconv滤波器的有效性，我们对当前的各种体系结构进行了大量的实验。我们用提议的架构替换了这些架构中的标准卷积滤波器。我们使用resnet-34、resnet-50和vgg-16体系结构对imagenet进行了三次大规模实验。我们已经为vgg-16、resnet-56和mobilenet体系结构展示了三个关于cifar-10的小规模实验。在所有实验中，我们都将挤压和激励（SE）的减速比设置为8。

4.1. Notations（符号）

XXX_P\(\alpha\)：\(XXX\)是架构，部分值是\(P =\alpha\); XXX_P\(\alpha\) _ SE：\(SE\)为挤压和激励，减速比= 8；XXX_GWC\(\beta\) _ PWC：GWC\(\beta\) _ PWC}是具有组大小\(\beta\)的分组卷积，然后是逐点卷积；​XXX_DWC_PWC：​DWC_PWC是深度卷积，然后是逐点卷积；XXX_PC：​PC是部分值\(P =输入通道数（输入深度）\)。

4.2. VGG16 on CIFAR10

在本实验中，我们使用了VGG-16架构的。在CIFAR-10数据集中，每个图像大小在RGB尺度上都是\(32\times 32\)大小。在VGG-16架构中，有13个卷积层使用标准的CONV2D卷积，每层之后我们都添加了批处理归一化。我们使用的设置与中描述的相同。超参数的值为:权值衰减=5e-4，批大小=128，初始学习率=0.1，每隔50个时点后按\(10 \times 0.1\)计算。

除了初始卷积层（即conv 1），其余12个标准卷积层都被我们的hetconv层（所有12个层的\(p\)值相同）所取代，同时保持与之前相同的文件数量。如表1所示，\(P\)值增大，FLOPs(计算)值减小，但精度没有明显下降。我们也用\(SE\)技术对HetConv进行了实验，发现\(SE\)在开始时提高了精度，但后来由于过拟合，开始降低模型性能(精度)，如表1所示。

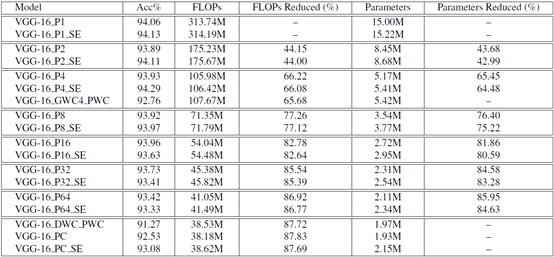
表格1 下表显示了不同设置下CIFAR-10上的VGG-16的详细结果。

4.2.1 Comparison with groupwise followed by pointwise convolution（与分组然后逐点卷积比较）

我们用分组进行逐点卷积，其中所有标准卷积层（除了初始卷积层，即CONV 1）由两层（具有组大小4和逐点卷积层的分组卷积层）代替。 现在模型有延迟一个。 如表-1所示，VGG-16 GWC4 PWC具有92.76％的准确度，而我们的VGG-16 P4型具有显着更高的93.93％准确度和更低的FLOP。

4.2.2 Comparison with depthwise followed by pointwise convolution（与深度方式，然后是逐点卷积的比较）

我们用深度方式进行实验，然后进行逐点卷积，其中所有标准卷积层（初始卷积层除外，即CONV 1）由两层（深度卷积层和逐点卷积层）代替。 现在模型有延迟一个。 如表1所示，VGG-16_DWC_PWC在CIFAR-10上的准确度仅为91.27％，而我们的VGG-16_P64型具有相当的FLOPs，精度高达93.42％。

我们还尝试了不同层的不同P值。 除了初始卷积层（即CONV 1）之外，所有剩余的12个标准卷积层都被我们的HetConv层替换，其中P =输入通道的数量。 如表1所示，我们的模型VGG-16 PC和VGG-16_PC_SE仍然表现优于VGG-16_DWC_PWC，这表明我们的HetConv优于DWC + PWC。

4.2.3 Comparison with FLOPs compression methods（与FLOPs压缩方法的比较）

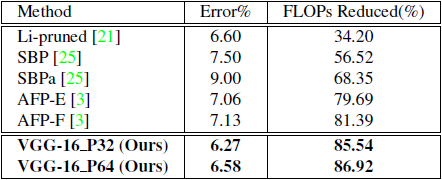
表格2 该表显示了我们的模型与CIFAR-10数据集上VGG-16架构的最新模型压缩方法的比较。

如表-2所示，与现有技术的模型压缩方法相比，我们的模型VGG-16 P32和VGG-16 P64具有明显更高的精度。 我们降低了~85％的FLOP而没有精度损失，而FLOPs压缩方法的准确性损失很大（超过1％），如表-2所示。

4.3. ResNet56 on CIFAR10（ResNet56在CIFAR10上）

我们在CIFAR-10数据集上试验了ResNet-56架构[8]。 ResNet-56由大小为16-32-64的卷积层的三个阶段组成，其中每个阶段的每个卷积层包含相同的2.36M FLOP，总FLOP为126.01M。我们使用相同的参数训练模型。[8]。 除了初始卷积层之外，所有剩余的标准卷积层都被我们的HetConv层替换，同时保持滤波器的数量与之前相同。

如表-3所示，与具有更高FLOP降低的现有模型压缩方法相比，我们的模型ResNet-56_P2和ResNet-56_P4具有明显更好的精度。 我们还使用SE技术对HetConv进行了实验，发现由于过度拟合，SE性能不如预期。

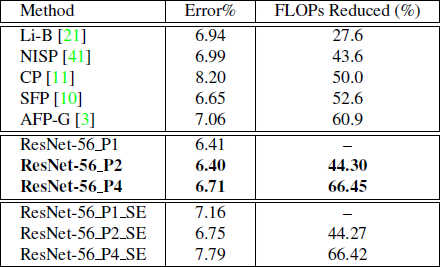
表格 3 下表显示了不同设置下ResNet-56与CIFAR- 10上的最新模型压缩方法的详细结果和比较。

4.4. MobileNet on CIFAR10（MobileNet在CIFAR10上）

该表显示了详细结果，并与不同设置中CIFAR-10上ResNet-56的最新模型压缩方法进行了比较。早些时候。 在我们的模型中，两个卷积层（深度卷积层和逐点卷积层）被一个HetConv卷积层取代，这将延迟从1减少到零。

如表4所示，我们的模型MobileNet_P32和MobileNet_P32_SE与MobileNet模型相比具有显著的更好的精度(接近1%)，而MobileNet架构上的失败几乎相同，这再次表明我们提出的HetConv卷积优于深度卷积和点态卷积。

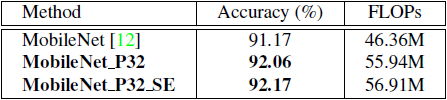
表格4 下表显示了在CIFAR- 10上不同设置下MobileNet的结果。

4.5. VGG16 on ImageNet

我们在大型ImageNet数据集上试验了VGG-16架构。 除了初始卷积层之外，所有剩余的卷积层都被我们的HetConv层替换，同时保持文件管理器的数量与之前相同。
我们的模型VGG-16_P4显示了最近针对翻转压缩提出的方法的最新结果。 通道修剪（CP）具有50.0％的FLOP压缩，而我们具有65.8％的FLOP压缩而没有精度损失。
有关更多详细信息，请参阅表-5。

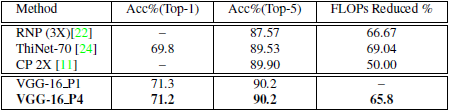
表格5 表中显示了ImageNet上VGG-16的结果。与目前最先进的剪枝方法相比，我们的模型在精度上没有损失，同时显著提高了FLOPs减少率。

4.6. ResNet-34 on ImageNet

我们在大型ImageNet数据集上试验了ResNet-34架构。 除了初始卷积层，所有剩余的卷积层都被我们的HetConv层替换。我们的模型ResNet-34_P4显示了先前提出的方法的最新结果。 NISP的FLOP压缩率为43.76％，而FLOP压缩率为64.48％，精度明显提高。 有关详细信息，请参阅表-6。

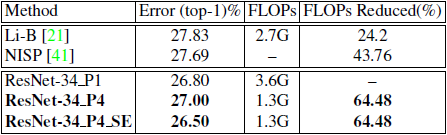
表格 6 表中显示了ResNet-34在ImageNet上的结果。与最先进的剪枝方法相比，我们的模型在精度上没有损失，而在不同的设置中显著提高了故障减少。

4.7. ResNet50 on ImageNet

ResNet-50是一种深度卷积神经网络，具有50层的残差连接。在这种结构中，我们用我们提出的HetConv卷积替换标准卷积。超参数的值为：权值衰减=1e-4，批大小=256，初始学习率=0.1，每隔30个epoch进行一次十进0.1，模型在90个epoch进行训练。

由表7可以看出，我们的模型ResNet-50_P4在精度上没有损失，而触发器剪枝方法在前1精度上存在较大的精度下降。我们的模型是从零开始训练的，但是剪枝方法需要预先训练的模型，并且涉及迭代剪枝和微调，这是一个非常耗时的过程。

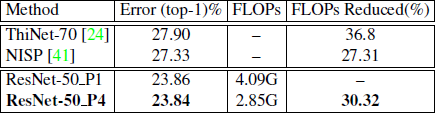
表格7 表中显示了ResNet-50在ImageNet上的结果。与现有的触发器剪枝方法相比，我们的模型在精度上没有损失。

5. Conclusion

在这项工作中，我们提出了一种使用异构内核的新型卷积。 我们将我们提出的卷积与各种现有架构（VGG-16，ResNet和MobileNet）上的流行卷积（深度卷积，分组卷积，逐点卷积和标准卷积）进行了比较。实验结果表明，与现有的卷积相比，我们的HetConv卷积更有效（较小的FLOP，精度更高）。由于我们提出的卷积不会增加层（替换具有多个层的层，例如，MobileNet）以减少FLOP，因此延迟为零。 我们还将基于HetConv卷积的模型与FLOPs压缩方法进行了比较，结果表明，与压缩方法相比，它可以产生更好的结果。 将来，使用这种类型的卷积，我们可以设计出更高效的架构。