相机IMU融合四部曲（三）:MSF详细解读与使用
极品巧克力
前言
通过前两篇文章，《D-LG-EKF详细解读》和《误差状态四元数详细解读》，已经把相机和IMU融合的理论全部都推导一遍了。而且《误差状态四元数》还对实际操作中的可能遇到的一些情况，进行指导。
这些理论都已经比较完整了，那么，该如何在实际当中操作呢？该如何用到实际产品中呢？误差状态四元数，是有开源的程序的，但是它是集成在rtslam（ https://www.openrobots.org/wiki/rtslam/ ）里面的，不方便提取出来使用。
但还有另外一个开源的程序，ETH的MSF（https://github.com/ethz-asl/ethzasl_msf），它是独立的一个开源程序，可以比较方便地用在自己的工程里面，并且它的理论与误差状态四元数很接近，稍微有点不同，所以MSF开源程序就成了一个不错的选择。
所以，我把MSF的程序全部都通读一遍之后，结合程序来推导MSF的理论，总结成本文，包括MSF的实验，与各位分享。
1.基本模型
基本模型如下图所示。
MSF的可扩展性很好，程序里可以接入新的传感器，比如GPS，激光雷达，码盘等。
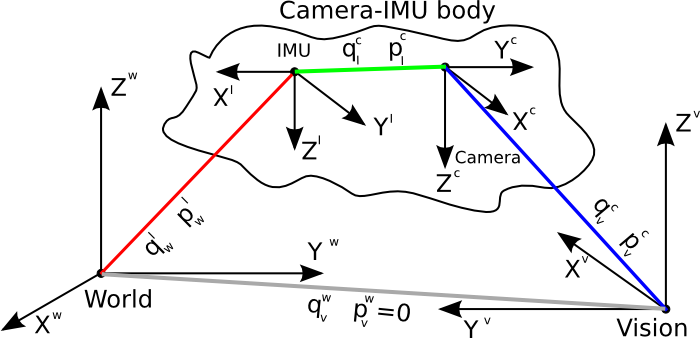
主要的理论还是误差状态四元数里面的理论。
相比于《卡尔曼四元数带外参融合方法》，它的方法更好。
首先，它的核心状态里面没有重力在世界坐标系下的表示。因为它用的就是《误差状态四元数》里面的5.3.1的方法，直接就是以水平坐标系为世界坐标系。只是初始位置根据当前加速度计的测量值和理论重力计算出来，初始位置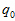
带着一个协方差而已。因为反正最后都是要转换到水平坐标系下的，所以这种方法反而更加方便。
而且，IMU的世界坐标系和相机的世界坐标系，也不用绑在一起，同时建立。可以在IMU开启一小段时间以后，相机再获取它的世界坐标系。但相隔时间应该还是要尽量短点，因为位移单靠IMU的加速度计的积分，时间久了会很不准确，如果有轮子码盘的话，则又可以好一些。调整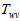
的目的，可能是因为世界坐标系和相机的世界坐标系，在时间戳上并不对应得很好，所以需要微调。
或者，为了避免这样的麻烦，直接把IMU的世界坐标系和相机的世界坐标系，绑在一起，同时建立。这样子，
。
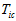也应该用ETH的手眼标定方法，借用棋盘格先标定好，再固定住。
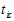就直接用尺子量好，固定住。如果用双目相机的话，就不用考虑
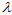了。
（如果加上轮速计的话，怎么更新呢？它的作用与IMU是相同的，都是相对值，而不是绝对值。所以，它应该与IMU实时融合，在主状态与相机融合后，IMU预测出一个位姿态，轮速计预测出一个位姿，然后两者融合出主状态。只有主状态才能与相机位姿融合。融合的话，可以用误差状态的思想来融合。）
所以，参考《误差状态四元数详细解读》，一个简单鲁棒的IMU与相机融合的模型应该是这样的。
核心状态为，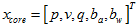
。
核心状态上的扰动为，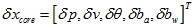
。
运动模型跟《误差状态四元数》里面的一样，
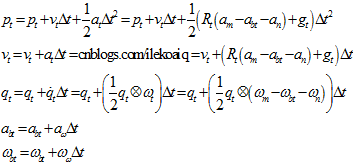
则相机位姿的观测方程为，
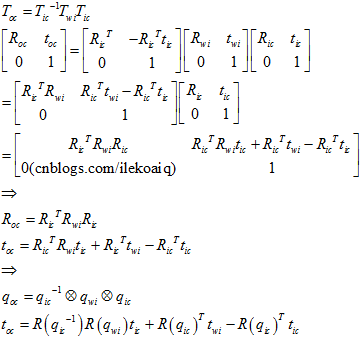
使用《误差状态四元数》里面的公式，
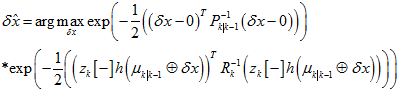
其中，
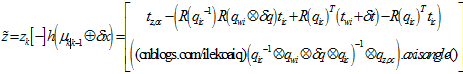
首先，要计算第一项关于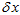
的雅克比，
则用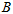
表示上式，则雅克比计算如下，
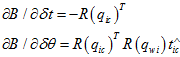
然后，第二项，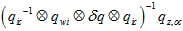
要转成三个元素的形式，即角轴李代数的形式。
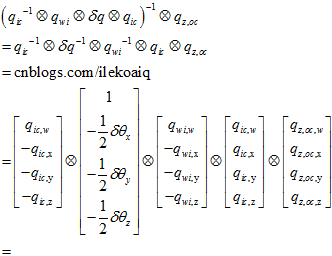
用matlab程序，解出上面的式子，以及关于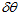
的雅克比。
syms qicw qicx qicy qicz thetax thetay thetaz ...
qwiw qwix qwiy qwiz qzocw qzocx qzocy qzocz real
q1=[qicw,-qicx,-qicy,-qicz]';
q2=[1,-1/2*thetax,-1/2*thetay,-1/2*thetaz]';
q3=[qwiw,-qwix,-qwiy,-qwiz]';
q4=[qicw,qicx,qicy,qicz]';
q5=[qzocw,qzocx,qzocy,qzocz]';
temp = quaternion_mul(q1,q2);
temp = quaternion_mul(temp,q3);
temp = quaternion_mul(temp,q4);
temp = quaternion_mul(temp,q5);
temp
J=jacobian(2*temp(2:4,:),[thetax,thetay,thetaz])
simplify(J)
雅克比可以是，把temp转换成角轴，再关于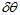
求导。或者，角轴直接近似等于temp向量部分的2倍，再关于
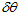求导，像上面的matlab程序这样。
这样子计算虽然准确，但是太麻烦了。论文里还用了近似的方法。为了方便地求雅克比，认为测量值近似为预测值直接转换出来，即，
。
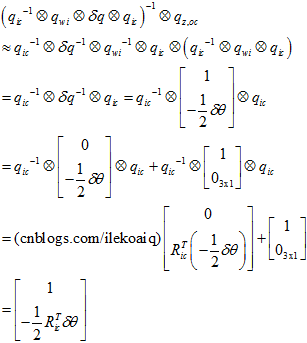
这时候，上式转换成角轴，就是，向量部分的2倍，即，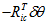
。所以，雅克比为，
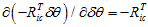
（这种用近似的方法，来算雅克比，虽然不如从原始公式上推导准确，但是可以极大地简化计算，也许可以给D-LG-EKF里面计算H矩阵时借鉴。）
所以，就得到了雅克比矩阵
。
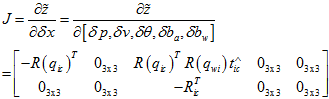
然后，
。就可以计算了。其余的流程，就跟《误差状态四元数》里面一样了。
2.对延时的处理
前提条件是，各个传感器的时间戳得是同一个时间源的，或者，时间戳很稳定，可以通过一些方法把它们时间戳之间的对应关系找到。不同传感器的时间戳能准确对应上。
然后，因为测量值有时候会过一段时间才处理完，所以，把滤波中的状态都记录起来，然后，当有测量值过来的时候，更新对应时刻的状态。然后继续往后预测。如果有多个不同传感器的测量值，也是如此操作。
3.计算相对测量
如果要融合单目相机。考虑到单目尺度的情况，怕有时候尺度会突然发生变化。为了应对这种情况，就都计算相对测量，就是两个时刻之间的相对位姿态，这样子，这一段的尺度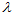
就可以滤得比较准确。然后，再把优化后的值，加入到原来的状态中，方法跟《误差状态四元数》中的传播差不多，就是把新滤出来的这段位姿的均值和扰动，加到原先状态的均值和扰动中去，整合出新的均值和扰动。
而如果要融合的是轮子码盘的话，则不必用这样的方法。因为虽然轮子码盘也有尺度问题，但是尺度是较稳定的。
如果是双目相机的话，也不必考虑这种尺度突然变化的情况。
4.准确地计算每帧的协方差
为了更好地与GPS融合，就需要当前状态需要有准确的协方差。
而以前计算出来的相机位姿的协方差是不准确的，没有考虑到累积误差造成的影响。造成了与IMU融合后的状态协方差也是不准确的。得准确地计算出要融合的每帧图像的协方差。这协方差，就是通过全局BA的方法，计算出来的。
但其实为了简化。如果真的要与GPS融合的话。
在即时建图的情况下，用上一段的方法。但是视觉的误差累积还是很可观的，所以如果是远距离的话，应该以GPS为外界绝对测量，视觉只是用来计算相对测量的。只能用短距离的视觉相对测量。在主状态之后，以此为起点，视觉的相对测量值与IMU的相对测量值融合，融合出相对测量状态，再把相对状态的均值和扰动合并进主状态以及主状态扰动，主状态再与GPS融合，融合出新的主状态。融合的话，可以用误差状态的思想来融合。
如果已经提前建图，回环检测都做了，地图点固定且准确了，则视觉协方差就是当前帧的协方差，不必通过全局BA算出。
5. MSF方法总结
MSF的方法考虑得很全面，这个理论框架，可以用来融合多种传感器。
我上面思考出来的方法，还考虑了与轮速计码盘，GPS融合的具体操作情况，以后需要时再用。
6.实验与改进
MSF的安装与跑例程，可以参考这篇文章，
然后，我自己用ORBSLAM2跑Euroc的V201数据集，生成轨迹数据，和IMU数据一起送入到MSF中运行。为什么要跑标准数据集呢？因为标准数据集提供了IMU噪声的真实参数，可以直接拿来使用，而且有真实的轨迹，groundtruth，可以用来评价融合结果的好坏。
可是运行结果却总是发散，融合后的轨迹锯齿非常严重。可是在理论上来讲，它应该能取得比较好的效果的呀？所以猜测应该是程序与理论没有对应上。
只好从程序里去查问题的原因。将程序里的所有的计算过程与算法公式一一对应起来之后，最终发现，是由程序里的2个地方导致的。
1.MSF程序有个隐含的假设，即图像的世界坐标系是水平的。而我送的是以第一帧为世界坐标系的，而V201的第一帧并不是水平的。
2. 经过仔细推导程序的计算过程，发现MSF程序中的qwv，本质上是qvw，这个导致参数的初值给错了。
将以上两个问题改过来之后，MSF就可以正常运行我自己提供的数据了。
其中，在y轴上的结果如下。
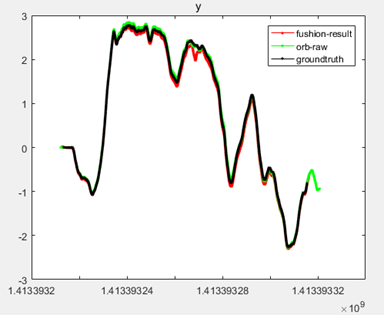
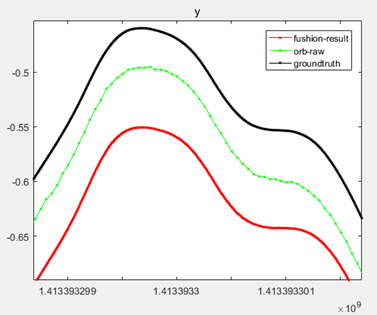
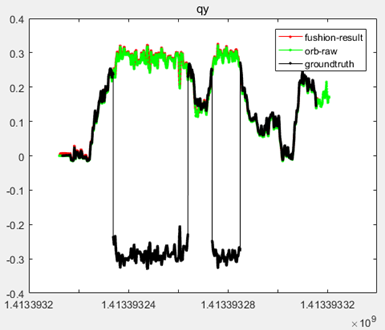
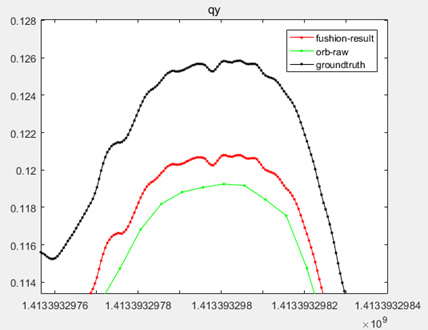
以上，黑色的线是真实值，绿色的线是ORBSLAM通过图像计算出来的位姿，红色的线是图像位姿和IMU融合后的结果，线上的每一个点都代表一个输出数据。可以看出，msf融合后的结果，不仅可以把位姿的输出频率提高到和IMU一样的频率，还可以让轨迹更加接近真实值。
但是，msf有一个缺点，那就是IMU的bias收敛得很慢，猜测是由于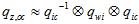
近似造成的。如下图所示。
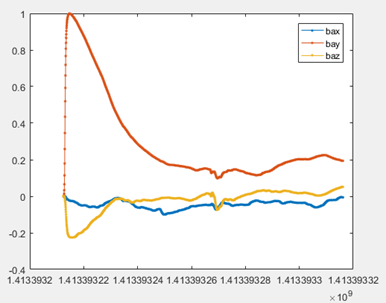
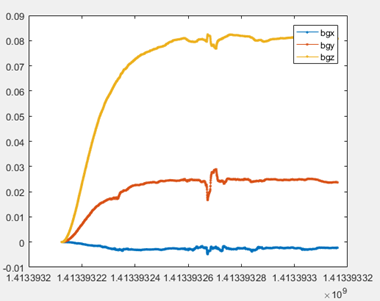
上图是加速度计的bias的收敛情况，和陀螺仪的bias的收敛情况。也许可以通过修改这部分的公式，让bias收敛得更快。
7.参考文献
-
Lynen S, Achtelik M W, Weiss S, et al. A robust and modular multi-sensor fusion approach applied to MAV navigation[C]// Ieee/rsj International Conference on Intelligent Robots and Systems. IEEE, 2013:3923-3929.
