数据结构笔记之（1）——树的三种遍历

转载请注明：http://www.cnblogs.com/igoslly/p/7864406.html

树的三种遍历

　　当接触树后，自然而然会接触树的遍历。

　　　　树的遍历共分为3种：先序遍历、中序遍历、后序遍历，这里的“序”为根节点的遍历顺序；

　　故而遍历顺序可理解为：

　　　　先序遍历：根节点 →左子树 → 右子树，在子树中继续应用左子树 → 根节点 → 右子树；

　　　　中序遍历：左子树 → 根节点 → 右子树，同理

　　　　后序遍历：左子树 → 右子树 → 根节点，同理

 

　　那如此抛出一个问题：给定树后确定遍历序列，那能否从遍历序列恢复原树呢？

　　　　单一遍历序列的话，答案肯定是否定的 —— 因为单孩子情况中无法确定为左孩子还是右孩子。

　　给定两个遍历序列的话，能否唯一确定呢？

　　　　1、先序+中序： 先序最头找到根节点root，中序找到root所在的位置，序列[0,root-1]即为左子树，[root+1,length-1]即为右子树，如此递推；

　　　　2、中序+后序：后序最末找到根节点root，同理；

　　通过上面两种情况，可以发现：

　　　　先序遍历在确定树左、右子树情况时起到了至关重要的作用。

　　　　3、先序+后序：不唯一确定，因为根节点单孩子情况下，先序和后序并无分别。

 

　　那我们题目想实现的是：如果给出了先序序列和中序序列，代码如何去实现？

　　　　　　遍历和构建树的实现无非是递归函数，重要是确定递归结束的条件。

　　首先先给出是三种遍历方式的实现方式：

//先序遍历
void preOrder(Tree * bt){
      if(bt!=NULL){
           visit(bt->data);
           preOrder(bt->lChild);
           preOrder(bt->rChild);
    }       
}

//中序遍历
void inOrder(Tree * bt){
      if(bt!=NULL){
           inOrder(bt->lChild);
           visit(bt->data);
           inOrder(bt->rChild);
    }       
}

//后序遍历
void postOrder(Tree * bt){
      if(bt!=NULL){
           postOrder(bt->lChild);
           postOrder(bt->rChild);
           visit(bt->data);
    }       
}

 

　　在通过先序+中序的根节点分开法中，有人也将其称之为分而治之法，直接将序列分为左子树和右子树考虑：

　　　　　　也就是左子树 index from [ 0, root-1 ]，右子树 index from [ root+1, length-1 ]

　　下面给出的只是我不成熟的实现方法：

// 主函数main
// 给出先序序列、中序序列，大家可手动画一下树图
// 建立树，再后续遍历输出

int main(){
    int pre[]={1,2,3,4,5,6,7};
    int in[]={3,2,4,1,6,5,7};
    Tree * head=init();
    int put=0;
    createTree(pre,in,0,6,head,&put);
    post(head);
}

 

　　　　树的初始化方法即：设定一个空数据的head头结点

　　　　定义find函数，找到在中序遍历中根节点的所在位置root

Tree * init(){
    Tree * head=(Tree *)malloc(sizeof(Tree));
    head->left=NULL;
    head->right=NULL;
    return head;
}

int find(int in[],int x){
    int i=0;
    while(1){
        if(in[i]==x){
            cout<<x<<" in pre array's index is "<<i<<endl;
            return i;
        }
        i++;
    }
    return 0;
}

 

　　　　然后是递归主题部分，个人也觉得写的有点繁琐了，可以简单看看

void createTree(int pre[],int in[],int leftindex,int rightindex,Tree * head,int *put){
    int root=find(in,pre[*put]);
    head->data=pre[*put];
    // 只剩单一元素，返回上层结点 
    if(leftindex==rightindex){
        return;
    }
    if(root!=leftindex){
        Tree * p=(Tree *)malloc(sizeof(Tree));
        p->left=NULL;
        p->right=NULL;
        head->left=p;
        cout<<"Now looking for "<<head->data<<" 's leftChild in arrayindex [ "<<leftindex<<", "<<root-1<<" ], put ="<<*put<<endl; 
        (*put)++;
        createTree(pre,in,leftindex,root-1,p,put);
    }
    if(root!=rightindex){
        Tree * q=(Tree *)malloc(sizeof(Tree));
        q->left=NULL;
        q->right=NULL;
        head->right=q;
        cout<<"Now looking for "<<head->data<<" 's rightChild in arrayindex [ "<<root+1<<", "<<rightindex<<" ], put ="<<*put<<endl; 
        (*put)++;
        createTree(pre,in,root+1,rightindex,q,put);
    }
}

 

　　　　在程序中，我插入了许多实时显示运行状态的语句，方便更好地理解和调试；

　　　　就比如在下语句时，我原本写的是 * put++ ，使*put=0直接下函数取3，成功找出错误；

(*put)++;

　　　　可以看到完整的构建过程，由于put指针传递，值持续增加，当然可以采用全局或者静态变量形式；

 

---

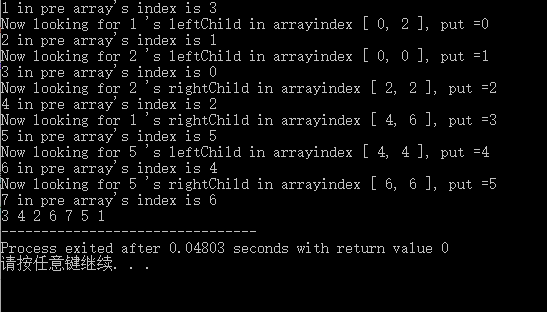
 申明：

1、本笔记为文字及图片均为个人原创，转载请注明博客园-igoslly

2、此题为2017年11月参与数据结构习题时实现