统计学——线性回归
笔记链接：http://www.cnblogs.com/igoslly/p/6790919.html
相关分析：测度变量之间的关系密切程度
回归分析：侧重考察变量之间的数量伴随关系
一元线性回归：只涉及一个解释变量，XY线性关系
模型：
称为误差项的随机变量，反映线性关系不能解释的变异性
基本假定
1、ε是期望值为0的随机变量
2、对于所有的x值，ε的方差相同
3、ε是服从正态分布、独立的随机变量
最小二乘法
若m为随机变量，则E(m-c)^2作为c的函数，在c=E（m）时达到最小；故而要以p(x)回归函数作为Y的近似，其均方误差E(p(x)-Y)^2为最小。
求偏导数可得：
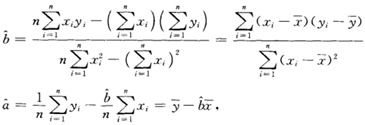
判定系数——对估计得回归方程拟合优度的度量。
总平方和 = 回归平方和 + 残差平方和 =（回归值-均值）平方和+（观测值-回归值）平方和
=线性关系因素+非线性关系因素
R=1，SSE=0，回归直线与各观测点越接近，回归直线的拟合程度越好。
相关系数 r = 平方根，|r|→1，直线拟合度越高
注:|r|≥，r看似大时，回归直线解释总变差的比率也并不高。
估计标准误差，类似标准差
剔除线性影响后，y随机波动大小的估计量
线性关系检验
多元线性分析
申明
本笔记在学习《统计学（贾俊平版）》整理所得，仅供学习使用，请勿转载
