统计学——单(双)因素方差分析
笔记链接:http://www.cnblogs.com/igoslly/p/6782963.html
方差分析(Analysis of Variance / ANOVA)
实验中,我们要考察的指标为试验指标,影响的条件成为因素。由于各种因素的影响,使得测试数据结果呈波动状,包含不可控的随机因素、人为调控的可控因素。
应用条件:
1、各样本是相互独立的随机样本
2、各样本均来自正态分布总体
3、各样本的总体方差相等,即具有方差齐性
单因素方差分析(one-way ANOVA)
试验参数
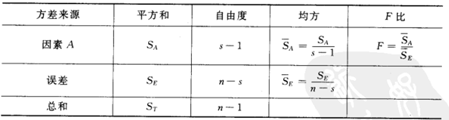
假设因素A有s个水平A1,A2…..,As,每个水平下进行nj次独立试验,样本总数n

观测变量总离差平方和 = 组间离差平方和 + 组内离差平方和,表述为:SST=SSA+SSE。
组内差异——测量误差、个体差异
SSE(误差平方和)各个水平下,样本观察值与样本均值差异的平方和
组内自由度 dfe=n-s
组间差异——不同实验条件处理
SSA(因素A的效应平方和)各个水平下样本平均值与数据总平均差异的平方和
组间自由度 dfa=s-1
均方 = 离差平方和 / 自由度 SA=SSA/dfa SE=SSE/dfe
单因素方差分析基本步骤
1、提出原假设:H0——无差异;H1——有显著差异
2、选择检验统计量:方差分析采用的检验统计量是F统计量,即F值检验
|
拒绝H0 |
F>F0.05(dfa,dfe) |
组间均方>>组内均方,来自不同正态总体 |
|
接受H0 |
F<F0.05(dfa,dfe) |
组间均方<<组内均方,来自相同正态总体 |
3、计算检验统计量的观测值和概率P值
4、给定显著性水平,并作出决策
方差齐性检验 ——对控制变量不同水平下各观测变量总体方差是否相等进行检验
控制变量不同水平下观测变量总体方差无显著差异是方差分析的前提要求。
若不满足,便不能认为各总体分布相同。
多重比较检验 ——控制变量的不同水平对观测变量的影响程度如何
实现对各个水平下观测变量总体均值的逐对比较
多(双)因素方差分析
单独效应 ——其他因素固定,某一因素不同水平之间均数的差别
交互效应 ——某因素的单独效应,随另一因素水平而变化,且不能用随机误差解释
试验参数
假设因素A有r个水平(A1,A2…..,Ar),因素B有s个水平(B1,B2……,Bs),每个ABzuhe进行t次独立试验,样本总数n



所有数据平均值μ,αi是水平Ai的效应,βj是水平Bj的效应,γij表示Ai与Bj的交互作用

同样计算离差平方和SST=SSA+SSE+SSB+SSAB
SSE(误差平方和)每个(ij)水平下测量值与均值差异的平方和
SSA、SSB(因素A\B的效应平方和)、SSAB(AB交互效应平方和)


例如双因素方差分析的基本步骤
1、提出原假设:
|
|
因素A(r) |
因素B(s) |
AB交互作用(rs) |
|
无显著差异 |
H01 |
H02 |
H03 |
|
有显著差异 |
H11 |
H12 |
H13 |
2、F值检验
|
拒绝H01 |
F0.05(dfa,dfe)<FA |
因素A不同存在显著差异 |
|
拒绝H02 |
F0.05(dfb,dfe)<FB |
因素B不同存在显著差异 |
|
拒绝H03 |
F0.05(dfab,dfe)<FAB |
因素A与B存在交互效应 |
补充:F分布
设X、Y为两个独立的随机变量,
X服从自由度为k1的卡方分布,Y服从自由度为k2的卡方分布
变量 F =(X / k1) / (Y / k2)服从F(k1,k2)的分布
学习资料来源
1、百度百科:方差分析
2、概率论与数理统计(第四版)
3、百度文库https://wenku.baidu.com/view/30a2bafc941ea76e58fa045a.html
申明
本笔记为个人整理,仅限学习使用,禁止转载


