摄像机、投影、3D旋转、缩放

2011-09-23 08:18 【当耐特】阅读(20732) 评论(64) 编辑收藏举报

简述

3D效果分两种，一种是伪3D骨架，一种是3D实体.

3D骨架：是通过大量的计算将3D世界中所有点投影到二维平面中。

3D实体:通过摄像机向投影面发射射线与世界中的物体交汇，把与物体交汇点的颜色渲染到投影面 （光线追踪的基础）。

本系列的所有演示都是3D骨架，非3D实体。本文将穿插图片、公式、代码、演示，让读者深刻理解3D的基本概念极其思想。

对象及概念介绍

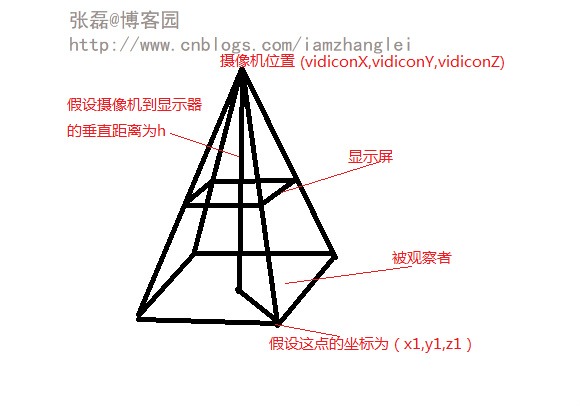
对象一：摄像机。

大家都有一个基本常识，在不同的角度观看到的物体是不同的。摄像机对象有自己的空间的坐标（vidiconX,vidiconY,vidiconZ）。

对象二：显示屏

任何三维物体，都会以二维的形式投影在显示屏上，显示屏垂直于摄像机的观测方向，所以摄像机的空间坐标变化，会导致显示屏的坐标系的变换。

对象三：被观察测物体

任何物体都是有无数个点构成，每个点有自己的空间坐标（x,y,z）,显示屏介于摄像机和物体之间。

为了降低复杂度，本文将显示屏和被观测物体所处的坐标系公用一套（x,y）,所有的旋转都是物体旋转，摄像机不动！

缩放原理：摄像机不动，被观察测物体不动，显示屏离摄像机越近，缩放比例越小，显示屏离摄像机越远，缩放比例越大。

投影分析

我们来看下面这张图：

因为，我们将显示屏和被观测物体共用一个坐标系，所以，我们可以计算出点（x1,y1,z1）投影到显示屏上的点的缩放比例为：

h / Math.abs(vidiconZ - z1)

所以投影后的坐标为：

x = x1 * h / Math.abs(vidiconZ - z);

y= y1 * h / Math.abs(vidiconZ - z);

有了以上这些知识，我们可以轻松的在Canvas里画一个正方体（再次强调，是根据计算的结果画，非人类经验）。

 <canvas id="myCanvas" width="700" height="500" style="border: 1px solid #c3c3c3;">
Your browser does not support the canvas element.
</canvas>
<script type="text/javascript">
    var c = document.getElementById("myCanvas");
    var cxt = c.getContext("2d");
    cxt.lineWidth = 3;
    //正方体8个顶点
    var Point1 = { x: 100, y: 100, z: 100 };
    var Point2 = { x: 100, y: 100, z: -100 };
    var Point3 = { x: -100, y: 100, z: -100 };
    var Point4 = { x: -100, y: 100, z: 100 };
    var Point_1 = { x: 100, y: -100, z: 100 };
    var Point_2 = { x: 100, y: -100, z: -100 };
    var Point_3 = { x: -100, y: -100, z: -100 };
    var Point_4 = { x: -100, y: -100, z: 100 };
    var startX = 250;
    var startY = 250;
    //摄像机到显示屏的距离
    var distance = 500;
    //摄像机位置
    var eyePosition = { x: 0, y: 0, z: 700 };
    function changeDistance() {
        Point1.x = Point1.x * distance / Math.abs(eyePosition.z - Point1.z);
        Point1.y = Point1.y * distance / Math.abs(eyePosition.z - Point1.z);
        Point2.x = Point2.x * distance / Math.abs(eyePosition.z - Point2.z);
        Point2.y = Point2.y * distance / Math.abs(eyePosition.z - Point2.z);
        Point3.x = Point3.x * distance / Math.abs(eyePosition.z - Point3.z);
        Point3.y = Point3.y * distance / Math.abs(eyePosition.z - Point3.z);
        Point4.x = Point4.x * distance / Math.abs(eyePosition.z - Point4.z);
        Point4.y = Point4.y * distance / Math.abs(eyePosition.z - Point4.z);
        Point_1.x = Point_1.x * distance / Math.abs(eyePosition.z - Point_1.z);
        Point_1.y = Point_1.y * distance / Math.abs(eyePosition.z - Point_1.z);
        Point_2.x = Point_2.x * distance / Math.abs(eyePosition.z - Point_2.z);
        Point_2.y = Point_2.y * distance / Math.abs(eyePosition.z - Point_2.z);
        Point_3.x = Point_3.x * distance / Math.abs(eyePosition.z - Point_3.z);
        Point_3.y = Point_3.y * distance / Math.abs(eyePosition.z - Point_3.z);
        Point_4.x = Point_4.x * distance / Math.abs(eyePosition.z - Point_4.z);
        Point_4.y = Point_4.y * distance / Math.abs(eyePosition.z - Point_4.z);
    }
    var drawCube = function () {
        changeDistance();
        cxt.beginPath();
        cxt.moveTo(startX + Point1.x, startY - Point1.y);
        cxt.lineTo(startX + Point2.x, startY - Point2.y);
        cxt.lineTo(startX + Point3.x, startY - Point3.y);
        cxt.lineTo(startX + Point4.x, startY - Point4.y);
        cxt.lineTo(startX + Point1.x, startY - Point1.y);
        cxt.moveTo(startX + Point_1.x, startY - Point_1.y);
        cxt.lineTo(startX + Point_2.x, startY - Point_2.y);
        cxt.lineTo(startX + Point_3.x, startY - Point_3.y);
        cxt.lineTo(startX + Point_4.x, startY - Point_4.y);
        cxt.lineTo(startX + Point_1.x, startY - Point_1.y);
        cxt.moveTo(startX + Point2.x, startY - Point2.y);
        cxt.lineTo(startX + Point_2.x, startY - Point_2.y);
        cxt.moveTo(startX + Point1.x, startY - Point1.y);
        cxt.lineTo(startX + Point_1.x, startY - Point_1.y);
        cxt.moveTo(startX + Point3.x, startY - Point3.y);
        cxt.lineTo(startX + Point_3.x, startY - Point_3.y);
        cxt.moveTo(startX + Point4.x, startY - Point4.y);
        cxt.lineTo(startX + Point_4.x, startY - Point_4.y);
        cxt.stroke();
    }
</script>
<div id="show">
</div>
<input type="button" onclick="drawCube();" value="开始画立方体"
style="width: 135px" />

演示

当然我们可以重构一下，将8个点都放到Array中。

 <script type="text/javascript">
     var c = document.getElementById("myCanvas");
     var cxt = c.getContext("2d");
     cxt.lineWidth = 3;
     //正方体8个顶点
     var Point = new Array();
     Point[0] = { x: 100, y: 100, z: 100 };
     Point[1] = { x: 100, y: 100, z: -100 };
     Point[2] = { x: -100, y: 100, z: -100 };
     Point[3] = { x: -100, y: 100, z: 100 };
     Point[4] = { x: 100, y: -100, z: 100 };
     Point[5] = { x: 100, y: -100, z: -100 };
     Point[6] = { x: -100, y: -100, z: -100 };
     Point[7] = { x: -100, y: -100, z: 100 };
     var startX = 250;
     var startY = 250;
     //摄像机到显示屏的距离
     var distance = 500;
     //摄像机位置
     var eyePosition = { x: 0, y: 0, z: 700 };
     function changeDistance() {
         for (var i = 0; i < Point.length; i++) {
             Point[i].x = Point[i].x * distance / Math.abs(eyePosition.z - Point[i].z);
             Point[i].y = Point[i].y * distance / Math.abs(eyePosition.z - Point[i].z);
         }
     }
     var drawCube = function () {
         changeDistance();
         cxt.beginPath();
         cxt.moveTo(startX + Point[0].x, startY - Point[0].y);
         cxt.lineTo(startX + Point[1].x, startY - Point[1].y);
         cxt.lineTo(startX + Point[2].x, startY - Point[2].y);
         cxt.lineTo(startX + Point[3].x, startY - Point[3].y);
         cxt.lineTo(startX + Point[0].x, startY - Point[0].y);
         cxt.moveTo(startX + Point[4].x, startY - Point[4].y);
         cxt.lineTo(startX + Point[5].x, startY - Point[5].y);
         cxt.lineTo(startX + Point[6].x, startY - Point[6].y);
         cxt.lineTo(startX + Point[7].x, startY - Point[7].y);
         cxt.lineTo(startX + Point[4].x, startY - Point[4].y);
         cxt.moveTo(startX + Point[1].x, startY - Point[1].y);
         cxt.lineTo(startX + Point[5].x, startY - Point[5].y);
         cxt.moveTo(startX + Point[0].x, startY - Point[0].y);
         cxt.lineTo(startX + Point[4].x, startY - Point[4].y);
         cxt.moveTo(startX + Point[2].x, startY - Point[2].y);
         cxt.lineTo(startX + Point[6].x, startY - Point[6].y);
         cxt.moveTo(startX + Point[3].x, startY - Point[3].y);
         cxt.lineTo(startX + Point[7].x, startY - Point[7].y);
         cxt.stroke();
     }
</script>

现在，我们看到了正方体正常的显示在画布当中，那么我们现在来用演示证明一下缩放原理

缩放原理：摄像机不动，被观察测物体不动，显示屏离摄像机越近，缩放比例越小，显示屏离摄像机越远，缩放比例越大。

<script language="javascript" type="text/javascript" src="lib/uglifyjs-parser.js"></script>
<script language="javascript" type="text/javascript" src="src/jscex.js"></script>
<script language="javascript" type="text/javascript" src="src/jscex.builderBase.js"></script>
<script language="javascript" type="text/javascript" src="src/jscex.async.js"></script>
<!--[if IE]>
<script language="javascript" type="text/javascript" src="lib/json2.js"></script>
<script language="javascript">
Jscex.config.codeGenerator = function (code) { return "false || " + code; }
</script>
<![endif]-->
<canvas id="myCanvas" width="700" height="500" style="border: 1px solid #c3c3c3;">
Your browser does not support the canvas element.
</canvas>
<script type="text/javascript">
    var c = document.getElementById("myCanvas");
    var cxt = c.getContext("2d");
    cxt.lineWidth = 3;
    var Point = new Array();
    var startX = 250;
    var startY = 250;
    var distance = 500;
    var eyePosition = { x: 0, y: 0, z: 700 };
    function init() {
        Point[0] = { x: 100, y: 100, z: 100 };
        Point[1] = { x: 100, y: 100, z: -100 };
        Point[2] = { x: -100, y: 100, z: -100 };
        Point[3] = { x: -100, y: 100, z: 100 };
        Point[4] = { x: 100, y: -100, z: 100 };
        Point[5] = { x: 100, y: -100, z: -100 };
        Point[6] = { x: -100, y: -100, z: -100 };
        Point[7] = { x: -100, y: -100, z: 100 };
    }
    function changeDistance() {
        for (var i = 0; i < Point.length; i++) {
            Point[i].x = Point[i].x * distance / Math.abs(eyePosition.z - Point[i].z);
            Point[i].y = Point[i].y * distance / Math.abs(eyePosition.z - Point[i].z);
        }
    }
    var drawCube = function (increment) {
        cxt.clearRect(0, 0, 1200, 1200);
        init();
        distance += increment;
        changeDistance();
        cxt.beginPath();
        cxt.moveTo(startX + Point[0].x, startY - Point[0].y);
        cxt.lineTo(startX + Point[1].x, startY - Point[1].y);
        cxt.lineTo(startX + Point[2].x, startY - Point[2].y);
        cxt.lineTo(startX + Point[3].x, startY - Point[3].y);
        cxt.lineTo(startX + Point[0].x, startY - Point[0].y);
        cxt.moveTo(startX + Point[4].x, startY - Point[4].y);
        cxt.lineTo(startX + Point[5].x, startY - Point[5].y);
        cxt.lineTo(startX + Point[6].x, startY - Point[6].y);
        cxt.lineTo(startX + Point[7].x, startY - Point[7].y);
        cxt.lineTo(startX + Point[4].x, startY - Point[4].y);
        cxt.moveTo(startX + Point[1].x, startY - Point[1].y);
        cxt.lineTo(startX + Point[5].x, startY - Point[5].y);
        cxt.moveTo(startX + Point[0].x, startY - Point[0].y);
        cxt.lineTo(startX + Point[4].x, startY - Point[4].y);
        cxt.moveTo(startX + Point[2].x, startY - Point[2].y);
        cxt.lineTo(startX + Point[6].x, startY - Point[6].y);
        cxt.moveTo(startX + Point[3].x, startY - Point[3].y);
        cxt.lineTo(startX + Point[7].x, startY - Point[7].y);
        cxt.stroke();
    }
    var reduceDrawCubeAsync = eval(Jscex.compile("async", function () {
        //当摄像机到显示屏的距离大于750，退出循环·
        while (distance < 750) {
            drawCube(10);
            $await(Jscex.Async.sleep(100));
        }
    }));
    var magnifyDrawCubeAsync = eval(Jscex.compile("async", function () {
        //当摄像机到显示屏的距离小于150，退出循环·
        while (distance > 150) {
            drawCube(-10);
            $await(Jscex.Async.sleep(100));
        }
    }));
    var executeAsync = eval(Jscex.compile("async", function () {
        $await(reduceDrawCubeAsync());
        $await(magnifyDrawCubeAsync());
    }));
</script>
<div id="show">
</div>
<input type="button" onclick="executeAsync().start();" value="开始移动显示屏" style="width: 135px" />

可以看到，我们定义了两个异步任务reduceDrawCubeAsync 和magnifyDrawCubeAsync ，把它们放到executeAsync 队列当中，

他们会从上倒下，依次执行。

演示

3D旋转

上面讲了摄像机，投影以及缩放的原理以及实现，下面看旋转。

首先，在三维坐标系当中，任何角度的任何旋转可以拆分成三类：

a.绕X轴方向的旋转，此时，y和z发生变化，x不变。

b.绕Y轴方向的旋转，此时，x和z发生变化，y不变。

a.绕Z轴方向的旋转，此时，x和y发生变化，x不变。

那么x和z到底变化多少呢？我们可以看一下切面图，然后计算出坐标的变化！

或者我们也可以直接翻到大学教材书本第七章【三维旋转矩阵】：

我们拿绕y轴旋转为例子，如：

    //旋转
    function rotate(angle) {
        for (var i = 0; i < Points.length; i++) {
            var tempX = Points[i].x;
            Points[i].x = Points[i].x * Math.cos(angle) - Points[i].z * Math.sin(angle);
            Points[i].z = Points[i].z * Math.cos(angle) + tempX * Math.sin(angle);
        }
    }

我们要记住，旋转之后的坐标是在坐标系当中的坐标，我们还要讲其投影到显示屏，所以我们应当先旋转---再投影，顺序不能弄反。

定义一个角度转弧度：

    function degToRad(a) {
        return (a / (360 / (2 * Math.PI)));
    }

立方体颜色变化：

    function randomColor() {
        var arrHex = ["0", "1", "2", "3", "4", "5", "6", "7", "8", "9", "A", "B", "C", "D", "E", "F"]; var strHex = "#";
        var index;
        for (var i = 0; i < 6; i++) {
            index = Math.round(Math.random() * 15);
            strHex += arrHex[index];
        }
        return strHex;
    }

旋转控制核心，我们依然用Jscex：

   var currentAngle = 0;
    var drawCube2 = function () {
        cxt2.clearRect(0, 0, 1200, 1200);
        init();
        rotate(degToRad(currentAngle))
        changedistance2();
        cxt2.strokeStyle = randomColor();
        cxt2.beginPath();
        cxt2.moveTo(startX + Points[0].x, startY - Points[0].y);
        cxt2.lineTo(startX + Points[1].x, startY - Points[1].y);
        cxt2.lineTo(startX + Points[2].x, startY - Points[2].y);
        cxt2.lineTo(startX + Points[3].x, startY - Points[3].y);
        cxt2.lineTo(startX + Points[0].x, startY - Points[0].y);
        cxt2.moveTo(startX + Points[4].x, startY - Points[4].y);
        cxt2.lineTo(startX + Points[5].x, startY - Points[5].y);
        cxt2.lineTo(startX + Points[6].x, startY - Points[6].y);
        cxt2.lineTo(startX + Points[7].x, startY - Points[7].y);
        cxt2.lineTo(startX + Points[4].x, startY - Points[4].y);
        cxt2.moveTo(startX + Points[1].x, startY - Points[1].y);
        cxt2.lineTo(startX + Points[5].x, startY - Points[5].y);
        cxt2.moveTo(startX + Points[0].x, startY - Points[0].y);
        cxt2.lineTo(startX + Points[4].x, startY - Points[4].y);
        cxt2.moveTo(startX + Points[2].x, startY - Points[2].y);
        cxt2.lineTo(startX + Points[6].x, startY - Points[6].y);
        cxt2.moveTo(startX + Points[3].x, startY - Points[3].y);
        cxt2.lineTo(startX + Points[7].x, startY - Points[7].y);
        cxt2.stroke();
    }
    drawCube2()
    var rotateAsync = eval(Jscex.compile("async", function () {
        while (true) {
            currentAngle += 5;
            drawCube2();
            $await(Jscex.Async.sleep(100));
        }
    }));

演示

我们也可以让它绕着X轴旋转：

    for (var i = 0; i < Points4.length; i++) {
        var tempY = Points4[i].y;
        Points4[i].y = Points4[i].z * Math.sin(angle) - Points4[i].y * Math.cos(angle);
        Points4[i].z = tempY * Math.sin(angle) + Points4[i].z * Math.cos(angle);
    }

演示

因为任何角度的任何旋转可以拆分成三类，我们可以同时绕X轴和Y轴旋转：

    function rotate(angle) {
        for (var i = 0; i < Points2.length; i++) {
            var tempX = Points2[i].x;
            var tempZ = Points2[i].z;
            Points2[i].x = Points2[i].x * Math.cos(angle) - Points2[i].z * Math.sin(angle);
            Points2[i].z = Points2[i].z * Math.cos(angle) + tempX * Math.sin(angle);
        }
        for (var i = 0; i < Points2.length; i++) {
            var tempY = Points2[i].y;
            Points2[i].y = Points2[i].y * Math.cos(angle) - Points2[i].z * Math.sin(angle);
            Points2[i].z = tempY * Math.sin(angle) + Points2[i].z * Math.cos(angle);
        }
    }

演示

总结

本文介绍了摄像机、投影、旋转、缩放等概念，并加以实现。本文为了降低复杂度，摄像机的位置不变，在真实的场景当中，比如一些3D游戏，如魔兽世界，摄像机和物体是都可以改变位置。

刷新页面返回顶部

当耐特