[Tyvj模拟赛]运
运
题目
【问题背景】
zhx 和妹子们玩数数游戏。
【问题描述】
仅包含4或7的数被称为幸运数。一个序列的子序列被定义为从序列中删去若干个数, 剩下的数组成的新序列。两个子序列被定义为不同的当且仅当其中的元素在原始序列中的下标的集合不相等。对于一个长度为 N的序列,共有 2^N个不同的子序列。( 包含一个空序列)。一个子序列被称为不幸运的, 当且仅当其中不包含两个或两个以上相同的幸运数。对于一个给定序列,求其中长度恰好为 K 的不幸运子序列的个数, 答案 mod 10^9+7 输出。
INPUT
第一行两个正整数 N, K, 表示原始序列的长度和题目中的K。
接下来一行 N 个整数 ai, 表示序列中第 i 个元素的值。
OUTPUT
仅一个数,表示不幸运子序列的个数。(mod 10^9+7)
SAMPLE
INPUT1
3 2
1 1 1
OUTPUT1
3
INPUT2
4 2
4 7 4 7
OUTPUT2
4
数据规模与约定
对于50%的数据, 1 ≤N ≤ 16。
对于70%的数据, 1 ≤ N ≤ 1000, ai ≤ 10000。
对于100%的数据, 1 ≤ N ≤ 100000,K ≤ N, 1 ≤ ai ≤ 109。
解题报告
考试时打了dfs,本来以为能打前50分,结果读错题+打挂了,只拿了20= =
正解:
首先,我们想,幸运数在数据范围内最多有1022个(正确性显然,我们可以轻易地知道,在一位数中,幸运数只有4和7,而两位数中,幸运数有44,47,74,77,我们看出,其实幸运数就是由4和7组合出来的,废话,题目就是这么定义的,所以,在n位数中,就有2^n个幸运数,而显然,幸运数在数据范围内只能到9位,等比数列求和得到1022)。
那么我们可以预处理出来,我用的是dfs,然后我们就拥有了所有的幸运数,随便离散一下什么的,我们就成功的打出了一个表。
对于剩下不是幸运数的d个数来说,这就是个组合问题。所以总方案数为
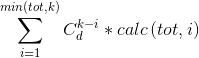
对于calc,随便dp一下就好了(可以当成01背包来做,很简单的,可以压成一维)
至于组合数,我们可以递推地求
(update:应某司机要求,讲一下如何递推地求组合数。)
我们知道

而

那么我们就有
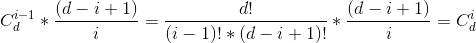
这就是我们的递推式,并且我们知道
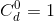
这就是我们的递推边界
剩下的,要注意,在模意义下的除法,是需要求逆元的
然后就很easy了
(update over)
具体看代码吧= =

1 #include<algorithm> 2 #include<iostream> 3 #include<cstring> 4 #include<cstdio> 5 using namespace std; 6 inline int read(){ 7 int sum(0); 8 char ch(getchar()); 9 for(;ch<'0'||ch>'9';ch=getchar()); 10 for(;ch>='0'&&ch<='9';sum=sum*10+(ch^48),ch=getchar()); 11 return sum; 12 } 13 typedef long long L; 14 const L mod(1000000007); 15 L n,k; 16 L n1; 17 L cnt,luc[1031]; 18 inline void dfs(int dep,int x){ 19 if(x) 20 luc[++cnt]=x; 21 if(dep==10) 22 return; 23 dfs(dep+1,x*10+4); 24 dfs(dep+1,x*10+7); 25 } 26 L sum[1031]; 27 L f[100001],c[100001]; 28 inline L pw(L x,L p){ 29 L ret(1); 30 while(p){ 31 if(p&1) 32 ret=(ret*x)%mod; 33 x=(x*x)%mod; 34 p>>=1; 35 } 36 return ret; 37 } 38 int main(){ 39 dfs(1,0); 40 sort(luc+1,luc+cnt+1); 41 n=read(),k=read(); 42 n1=n; 43 for(int i=1;i<=n;i++){ 44 int a(read()); 45 int pos(lower_bound(luc+1,luc+cnt+1,a)-luc); 46 if(luc[pos]==a){ 47 sum[pos]++; 48 if(sum[pos]==2) 49 n1-=2; 50 if(sum[pos]>2) 51 n1--; 52 } 53 } 54 c[0]=f[0]=1; 55 for(int i=1;i<=cnt;i++) 56 if(sum[i]>=2) 57 for(int j=i;j>0;j--) 58 f[j]=(f[j]+f[j-1]*sum[i])%mod; 59 for(int i=1;i<=n1;i++) 60 c[i]=c[i-1]*(n1-i+1)%mod*pw(i,mod-2)%mod; 61 L ans(0); 62 for(int i=0;i<=k;i++) 63 ans=(ans+c[i]*f[k-i]%mod)%mod; 64 printf("%lld",ans); 65 }



