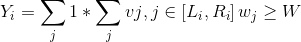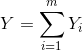[NOIP 2011]聪明的质监员
聪明的质监员
题目
小 T 是一名质量监督员,最近负责检验一批矿产的质量。这批矿产共有n个矿石,从 1 到n逐一编号,每个矿石都有自己的重量wi以及价值vi。检验矿产的流程是:
1. 给定 m个区间[Li,Ri];
2. 选出一个参数W;
3. 对于一个区间[Li,Ri],计算矿石在这个区间上的检验值Yi:
j是矿石编号。
这批矿产的检验结果Y为各个区间的检验值之和。即:
若这批矿产的检验结果与所给标准值 S 相差太多,就需要再去检验另一批矿产。小 T 不想费时间去检验另一批矿产,所以他想通过调整参数 W 的值,让检验结果尽可能的靠近标准值 S,即使得S−Y的绝对值最小。请你帮忙求出这个最小值。
INPUT
输入文件 qc.in。
第一行包含三个整数n,m,S,分别表示矿石的个数、区间的个数和标准值。
接下来的n 行,每行2 个整数,中间用空格隔开,第i+1 行表示i 号矿石的重量wi 和价值vi 。
接下来的m 行,表示区间,每行2 个整数,中间用空格隔开,第i+n+1 行表示区间[Li,Ri]的两个端点Li 和Ri。注意:不同区间可能重合或相互重叠。OUTPUT
输出文件名为qc.out。
输出只有一行,包含一个整数,表示所求的最小值。SAMPLE
INPUT
5 3 15
1 5
2 5
3 5
4 5
5 5
1 5
2 4
3 3OUTPUT
10
EXPLAIN
当W 选4 的时候,三个区间上检验值分别为20、5、0,这批矿产的检验结果为25,此时与标准值S 相差最小为10。
解题报告
考试时打了暴力- -,本来想到二分的,结果脑子一抽,以为单峰性,又不会打三分,只能爆炸- -
正解:
二分答案加验证
容易知道,当W增大时,满足条件的wi数目会减少,从而v会减少,我们就可以用这个作为二分条件,进行二分
在进行验证时,可以根据W建前缀和数组,以保证查询时的复杂度,剩下的就很简单了= =

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 typedef long long L; 6 inline L read(){ 7 L sum(0); 8 char ch(getchar()); 9 for(;ch<'0'||ch>'9';ch=getchar()); 10 for(;ch>='0'&&ch<='9';sum=sum*10+(ch^48),ch=getchar()); 11 return sum; 12 } 13 L ans(0x7fffffffffffffffLL),sum[200001],quan[200001],s; 14 int n,m; 15 int edge_mn(0x7fffffff),edge_mx(0); 16 int w[200001],v[200001]; 17 int l[200001],r[200001]; 18 inline L my_min(L a,L b){ 19 return a<b?a:b; 20 } 21 inline L my_max(L a,L b){ 22 return a>b?a:b; 23 } 24 inline void ST(int x){ 25 sum[0]=quan[0]=0; 26 for(int i=1;i<=n;i++){ 27 sum[i]=sum[i-1],quan[i]=quan[i-1]; 28 if(w[i]>=x) 29 sum[i]++,quan[i]+=v[i]; 30 } 31 } 32 inline L jdz(L x){ 33 return x>=0?x:-x; 34 } 35 inline bool judge(int u){ 36 ST(u); 37 L tmp(0); 38 for(int i=1;i<=m;i++) 39 tmp+=(sum[r[i]]-sum[l[i]-1])*(quan[r[i]]-quan[l[i]-1]); 40 ans=my_min(ans,jdz(tmp-s)); 41 if(tmp>s) 42 return true; 43 return false; 44 } 45 inline void ef(int l,int r){ 46 if(l==r) 47 return; 48 int mid((l+r)>>1); 49 if(judge(mid)) 50 ef(mid+1,r); 51 else 52 ef(l,mid); 53 } 54 inline int gg(){ 55 freopen("qc.in","r",stdin); 56 freopen("qc.out","w",stdout); 57 n=read(),m=read(),s=read(); 58 for(int i=1;i<=n;i++){ 59 w[i]=read(),v[i]=read(); 60 edge_mn=my_min(edge_mn,w[i]),edge_mx=my_max(edge_mx,w[i]); 61 } 62 for(int i=1;i<=m;i++) 63 l[i]=read(),r[i]=read(); 64 ef(edge_mn,edge_mx+1); 65 printf("%lld",ans); 66 } 67 int K(gg()); 68 int main(){;}