个人项目-地铁出行线路规划程序
欢迎大家关注我们的软工团队:http://www.cnblogs.com/Default1406/
PSP表格
| PSP 2.1 | Personal Software Process Stages | Planning Time(H) | Used Time(H) |
|---|---|---|---|
| Planning | 计划 | 0.5 | 0.25 |
| · Estimate | · 估计这个任务需要多少时间 | 0.5 | 0.25 |
| Development | 开发 | 25.5 | 45.9 |
| · Analysis | · 需求分析 (包括学习新技术) | 10 | 13 |
| · Design Spec | · 生成设计文档 | 2 | 3 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 0.25 | 0.1 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 0.25 | 0.1 |
| · Design | · 具体设计 | 2 | 4 |
| · Coding | · 具体编码 | 8 | 24 |
| · Code Review | · 代码复审 | 1 | 0.2 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 2 | 1.5 |
| Reporting | 报告 | 2 | 3 |
| · Test Report | · 测试报告 | 1 | 2 |
| · Size Measurement | · 计算工作量 | 0.5 | 0.5 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 0.5 | 0.5 |
| 合计 | 28 | 49.15 |
设计文档
需求分析
- 最短(经过站点数最少)路线查询,需要输出每次查询的详细路线与换乘情况。
- 换乘最少最短路线查询,需要输出每次查询的详细路线与换乘情况。
- 最快(经过站点数最少)遍历线路查询,需要输出遍历的详细路线。
- 用户只需要通过命令行进行以上三个操作。
功能设计
-
最短路线查询
在命令行中以
-b参数加两个地铁站点名称执行程序时,例如subway.exe -b station1 station2将计算从第一个站点station1到第二个站点station2的最短(经过的站点数最少)路线,并返回经过的站点的个数和路径,如果有换乘,请列出换乘的线路。输出格式如下:4 知春路 知春里 海淀黄庄换乘地铁十号线 中关村
-
换乘最少最短路线查询
在命令行中以
-c参数加两个地铁站点名称执行程序时,例如subway.exe -c station1 station2将计算从第一个站点station1到第二个站点station2的换乘最少的最短路线,并返回经过的站点的个数和路径,如果有换乘,请列出换乘的线路。输出格式同上。 -
最快遍历线路查询
扩展命令行程序,使其以
-a参数加一个地铁站点名称执行程序时,例如subway.exe –a station将计算从站点station出发,最快(经过的站点数最少,若一个站点经过多次需重复计算)地遍历地铁的所有车站的路线,要求
a.换乘不出地铁系统,即不能从一个地铁口走到路面,然后从另一个站进去;
b.只用经过一次,就算经过车站。
程序输出总共经过多少站,以及经过的站名。举例来说,假如地铁系统只有知春路和西土城两个站,从知春路站出发,那么这个程序应该输出:3 知春路 西土城 知春路
系统与模块设计
框架设计思路

建立三层系统架构。地图数据层用于读取文本中的地图信息,转化为使用邻接矩阵保存的图(Graph),并存储已查询过的路线信息以提高性能;线路规划层从交互控制层读取请求信息,使用相应算法对三种请求进行路线规划,并进行结果输出;交互控制层作为程序执行中心,进行相应的语法检查,转化字符串为相应请求数据传递给路线规划层。
模块设计
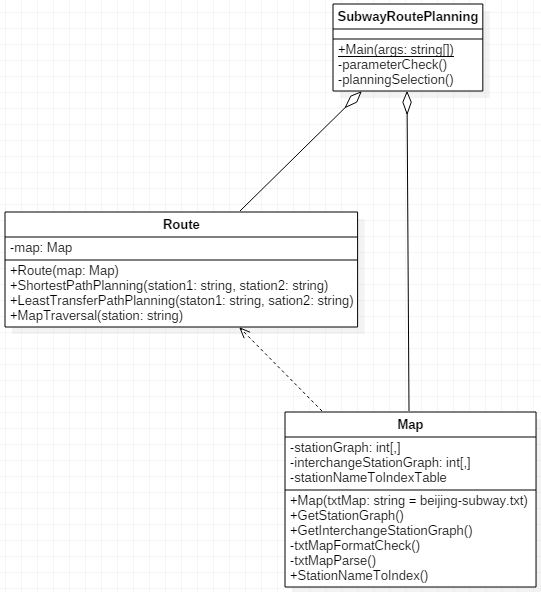
地图数据层(Map)
-
文本地图存储方式
文本地图存储了地铁线路名称、各个地铁站点的名称以及车站换乘信息。为了方便人工直接查阅和正则表达式的解析,采用了较为简洁的存储方式,模板如下:
@地铁线路名称 站点1 站点2[其它途经地铁线1][其它途经地铁线2……] …… 站点n以地铁1号线为例:
1号线 苹果园 古城 八角游乐园 八宝山 玉泉路 五棵松 万寿路 公主坟[10号线] 军事博物馆[9号线] 木樨地 南礼士路 复兴门[2号线] 西单[4号线] 天安门西 天安门东 王府井 东单[5号线] 建国门[2号线] 永安里 国贸[10号线] 大望路[5号线] 四惠[八通线] 四惠东[八通线] @2号线 ……注意地铁站名使用中文字符以外,其它所有字符均采用英文半角字符。站点信息中也应不存在空格符,比如
东单[ 5号线]。使用@标志来标记环形线路。且由于机场线较为特殊,简化为三元桥-2号航站楼-3号航站楼的路线设定。 -
文本与程序数据转换
对文本进行逐行读取,以2行为一个单位进行地铁信息录入,并存储于SubwayLine结构中。SubwayLine相关结构如下struct Station { public string Name; public bool IsTransferStation; public List<string> PlacedSubwayLineName; }; struct SubwayLine { public string Name; public List<string> InLineSubwayStationsNames; };
首先读取第一行的地铁线路名,然后使用空白符对第二行的站点信息进行切分。应用正则表达式对每个站点的信息进行提取,存入
SubwayLine结构中,然后合并所有SubwayLine为一个Hashtable SubwayLines的排序列表。结合所有路线信息,创建另一个排序列表SoretedList Stations实现站点名与邻接矩阵下标的对应关系,不会创建重复的站点名键。 -
地铁图(Graph)的生成
首先需要实现图的数据结构初步实现如下,
public StationsGraph(SortedList stations, Hashtable subwayLines) { this.stationVertexNum = stations.Count; this.stationVertices = stations; this.adjacencyMatrix = new int[stationVertexNum, stationVertexNum]; this.subwayLines = subwayLines; for (int i = 0; i < stationVertexNum; i++) { for (int j = 0; j < stationVertexNum; j++) { adjacencyMatrix[i, j] = -1; } } for (int i = 0; i < stationVertexNum; i++) { adjacencyMatrix[i, i] = 0; } SetAdjacencyMatrix(); }
通过遍历
SubwayLines排序列表读取每个站点所处所有线路的相邻站点信息,并且依据Stations的索引号实现邻接矩阵用于路线计算。需要建立两个地铁图,一个用于最短路径计算,一个用于最少换乘路径计算。
线路规划层(RoutePlanning)
-
最短路线规划
采用Floyd最短路径算法进行计算,这个方法较为简单,一次计算所有的路径后存储于矩阵中。更重要的是如何在Floyd路径矩阵中寻找完整的路径。实现方式如下:
private void searchCompletedShortestRoute(int station1Index, int station2Index, List<string> shortestRoute) { int shortestRouteInsertIndex; int pathStationIndex = routeMatrix[station1Index, station2Index][0]; if (pathStationIndex == -1) return; shortestRouteInsertIndex = shortestRoute.FindIndex((string stationName) => stationName == (string)map.Stations.GetKey(station2Index)); shortestRoute.Insert(shortestRouteInsertIndex, (string)map.Stations.GetKey(pathStationIndex)); searchCompletedShortestRoute(station1Index, pathStationIndex, shortestRoute); searchCompletedShortestRoute(pathStationIndex, station2Index, shortestRoute); }
采用了递归的方式,不断在两点之间寻找最短中转点,直到两个点为相邻点。这样就可以通过Floyd路径矩阵找到完整的路径了。
-
最少换乘路线规划
在这里又使用了递归的方式进行线路查找。首先在起始站点所在线路上搜索是否存在目标站点,如果存在则返回路径。否则,对这条地铁线上的所有中转站进行递归查找,查看下一个地铁线上是否存在目标站点。自此重复进行递归操作,知道查找到目标站点。值得注意的是,这里采用了两个方式优化性能。第一,对每层递归记录已经遍历的地铁线路,防止重复递归同一条线路。第二,采用了一个全局变量记录当前最浅的成功递归深度,进行剪枝操作,很大程度上优化了性能。
private void searchLeastTransferRoute(int curRecursiveDepth, string curStationName, string curSubwayLineName, string targetStationName, List<string> notRecursiveSubwayLines, List<string> leastTransferRoute) { List<string> inLineSubwayStationsNames = ((SubwayLine)map.SubwayLines[curSubwayLineName]).InLineSubwayStationsNames; List<string> newNotRecursiveSubwayLines = new List<string>(notRecursiveSubwayLines.ToArray()); List<string> newLeastTransferRoute = new List<string>(leastTransferRoute.ToArray()); newNotRecursiveSubwayLines.Remove(curSubwayLineName); newLeastTransferRoute.Add(curStationName); if (recursiveDepthLimit != -1 && curRecursiveDepth > recursiveDepthLimit) return; if (inLineSubwayStationsNames.Contains(targetStationName)) { recursiveDepthLimit = curRecursiveDepth; newLeastTransferRoute.Add(targetStationName); leastTransferRoutes.Add(newLeastTransferRoute); return; } foreach (string stationName in inLineSubwayStationsNames) { Station station = (Station)map.Stations[stationName]; if (station.IsTransferStation) foreach (string subwayLineName in station.PlacedSubwayLineName) if (newNotRecursiveSubwayLines.Contains(subwayLineName)) searchLeastTransferRoute(curRecursiveDepth + 1, stationName, subwayLineName, targetStationName, newNotRecursiveSubwayLines, newLeastTransferRoute); } return; }
而后,需要进行第一次筛选,找出包含最少换乘站点的路线。在此处递归得到路线只是包含了相应换乘地铁站与始末站点,还要获取完整的路线规划。不同于“最短线路规划”,我们要直接从线路信息中直接提取两个换乘站点间的所有站点信息。得到完整路径后,进行第二次筛选,这里我们将筛选出最少换乘中的最短路径。自此完成路线规划。
输入输出控制(IO Controller)
为了简化程序,直接使用程序的主类进行的控制。较为简单,对相应的请求类型进行处理。有一定的容错控制,防止崩溃。
代码规范
默认采用:微软编程规范
性能测试与优化
最短线路规划功能性能测试
-
性能分析图
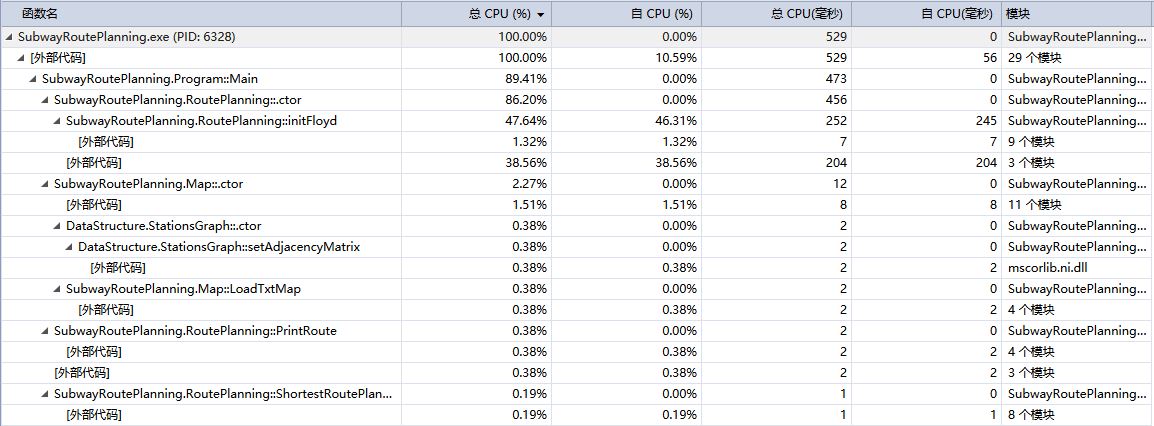
-
性能分析
容易看到使用
-b 南礼士路 新街口样例进行性能分析时,Floyd路径矩阵的生成(SubwayRoutePlanning.RoutePlanning::initFloyd)占据了将近一半的CPU消耗,消耗最大。这也比较符合O(n^3)的算法时间复杂度,是程序的核心算法部分。其它的外部代码算法,是相应的完整路径递归查找和相关的调用代码,虽然递归深度不是太深,但是一样消耗了40%的资源,足以看出递归的性能较为低下。
最少换乘最短线路规划功能性能测试
-
性能分析图
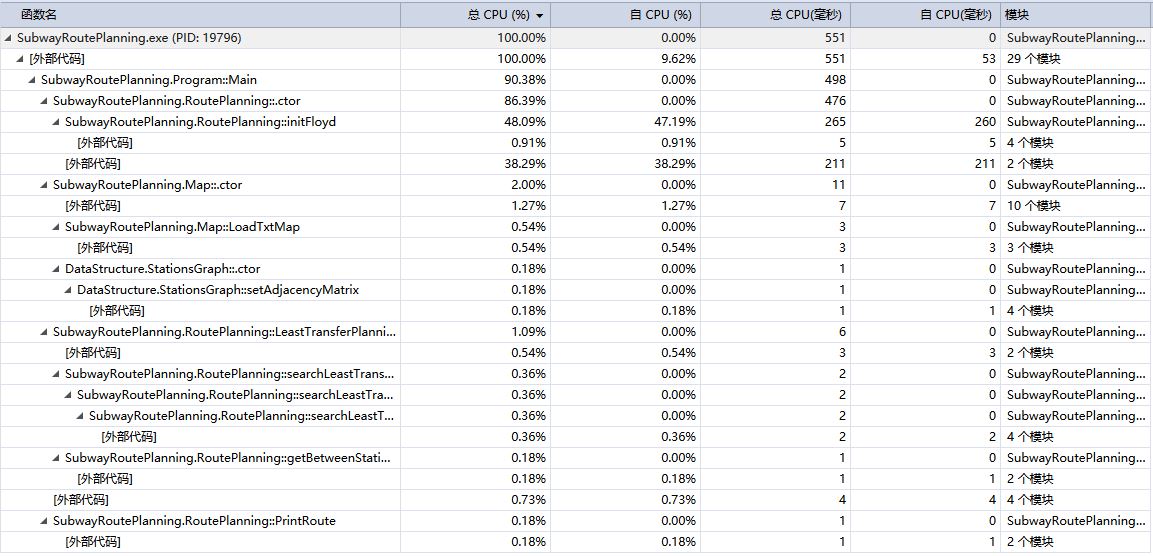
-
性能分析
基本与“最短线路规划”性能消耗分布一致,“SubwayRoutePlanning.RoutePlanning::initFloyd”是性能消耗最大的函数。在这个功能中使用“剪枝”的方式进行优化。通过测试发现,未优化前程序整体消耗为10936毫秒,是剪枝后的20倍,足以见得剪枝对程序整体的优化之大。
测试
最短线路规划功能测试
-
基本运行测试
-b 南礼士路 天安门西 4 南礼士路 复兴门 西单 天安门西
-
同线路换乘节点-换乘节点测试
-b 西直门 雍和宫 5 西直门 积水潭 鼓楼大街 安定门 雍和宫
-
单次换乘测试
-b 军事博物馆 车公庄 5 军事博物馆 白堆子 白石桥南换乘地铁6号线 车公庄西 车公庄
-
多次换乘测试
-b 南礼士路 新街口 6 南礼士路 复兴门换乘地铁2号线 阜成门 车公庄换乘地铁6号线 平安里换乘地铁4号线大兴线 新街口
-
双线并行线路测试
-b 大望路 高碑店 4 大望路 四惠 四惠东 高碑店
经测试发现换乘信息有误,双线并行情况需特殊处理。
4 大望路 四惠 四惠东换乘地铁八通线 高碑店
-
超长线路规划测试
-b 丰台东大街 望京东 22 丰台东大街 七里庄 六里桥换乘地铁10号线 莲花桥 公主坟换乘地铁1号线 军事博物馆换乘地铁9号线 白堆子 白石桥南换乘地铁6号线 车公庄西 车公庄换乘地铁2号线 西直门 积水潭 鼓楼大街换乘地铁8号线 安德里北街 安华桥 北土城换乘地铁10号线 安贞门 惠新西街南口 芍药居换乘地铁13号线 望京西换乘地铁15号线 望京 望京东
经仔细与北京地铁推荐线路比对,完全正确。
最少换乘最短线路规划测试
-
基本运行测试
-c 南礼士路 天安门西 4 南礼士路 复兴门 西单 天安门西
-
最少换乘对比最短路径测试
-c 南礼士路 新街口 7 南礼士路 复兴门 西单换乘地铁4号线大兴线 灵境胡同 西四 平安里 新街口
与最短线路规划的同一输入比较
-c 南礼士路 新街口,符合最少换乘最短路径的功能要求。 -
超长线路规划测试
-c 军事博物馆 惠新西街南口 17 军事博物馆 西钓鱼台换乘地铁10号线 慈寿寺 车道沟 长春桥 火器营 巴沟 苏州街 海淀黄庄 知春里 知春路 西土城 牡丹园 健德门 北土城 安贞门 惠新西街南口
经测试发现缺少
公主坟站,需要进行DEBUG。经过排查后发现是中间路径添加有误,遗漏添加无中间站的后继结点,修改后正确。17 军事博物馆 木樨地 南礼士路 复兴门 西单 天安门西 天安门东 王府井 东单换乘地铁5号线 灯市口 东四 张自忠路 北新桥 雍和宫 和平里北街 和平西桥 惠新西街南口
线路站点查询功能测试
10号线 *巴沟 *苏州街 *海淀黄庄 *知春里 *知春路 *西土城 *牡丹园 *健德门 *北土城 *安贞门 *惠新西街南口 *芍药居 *太阳宫 *三元桥 *亮马桥 *农业展览馆 *团结湖 *呼家楼 *金台夕照 *国贸 *双井 *劲松 *潘家园 *十里河 *分钟寺 *成寿寺 *宋家庄 *石榴庄 *大红门 *角门东 *角门西 *草桥 *纪家庙 *首经贸 *丰台站 *泥洼 *西局 *六里桥 *莲花桥 *公主坟 *西钓鱼台 *慈寿寺 *车道沟 *长春桥 *火器营
此项功能较为简单,容易进行测试。
项目总结学习
不得不说这次学习收获颇丰,只有在科学的方法论的指导下才能发挥最大的生产力。按照PSP表的步骤进行规划统筹,而不是一味地直接编码,真切地可以保持整体思路的清晰。总结了一下几点:
-
计划优先
到这个阶段的学习,不单单是对知识的探索,更多的是工作效率的提升。而任何工作都离不开计划和目标的设定,只有在具体的行动框架下才能规范自己的设计思路,督促自己完成每一个步骤。编码不是工作的一切,背后的思考与策划也十分重要。
-
适度放弃
必须要承认在有限的知识积累和时间下,有些事情是无法完成的。在附加题的设计与编码上花费了8个小时左右的时间,可是到最后还是没有设计出最优化的方案,存在很多缺陷,由于测试量巨大,也无法精准排错。最后不得不放弃附加题。我认为这已经浪费了大量的时间,基本上在2小时内无法设计出完整方案就应该放弃这个计划,转向其他工作,这一个小的模块不是整个程序的核心部件,可有可无。认清自己的实力和条件,适时放弃才是提高效率的王道。
-
文档化
博客的撰写对项目思路的整理和自我的学习提升有着很大的帮助,脑子里的思路不是思路,只有能表达总结文档,甚至要考虑到别人能否从中有所收获才是真正地思考成果。而且这是对一个项目的总结,对自我的一种反馈,激发自己继续提升。
-
算法应用
程序中用到了图相关的数个算法,不算难,但也是对过往学习的一次回顾。Folyd算法、递归查找、剪枝策略都是一次又一次的算法实操,重复融合实际应用与理论知识,认识到了理论知识对实际工程的重要性。要做一名优秀的软件工程师,必须要有足够的数学与计算机理论,才能在这条路上远走越远,而不是流于技术的表面。
-
技术速成
为了软件工程课程顺利进行快速学习了博客搭建、C#快速入门、项目配置、Markdown与HTML入门语法,虽然只是些皮毛但是随着问题的出现和解决,对技术的积累也在不断加深。在这个快速发展的时代,只有快速地学习才能适应身边环境的变迁。
欢迎关注我的个人博客:www.beyondbin.com




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步