图

1.学习总结(2分)

1.1图的思维导图

 

1.2 图结构学习体会

• 深度遍历算法：这个遍历过程是个递归过程，以邻接矩阵为存储结构，调用DFS函数
• 广度遍历算法：将图中所有和初始顶点v有路径相通的顶点都被访问，以邻接矩阵为存储结构
• Prim和Kruscal算法：Prim算法是一种构造性算法，算法中有两重for循环，更适合稠密图求最小生成树；
•                                   Kruskal算法是一种求带权无向图的最小生成树的构造性算法，按权值的递增次序选择合适的边来构造最小生成树，更适合稀疏图求最小生成树
• Dijkstra算法：单源最短路径问题，

  利用dist和path求最短路径长度和最短路径

• 拓扑排序算法：在一个有向图中找一个拓扑序列的过程称为拓扑排序

2.PTA实验作业（4分）

---

2.1 题目1：

7-1 图着色问题

2.2 设计思路（伪代码或流程图）

 

 

 

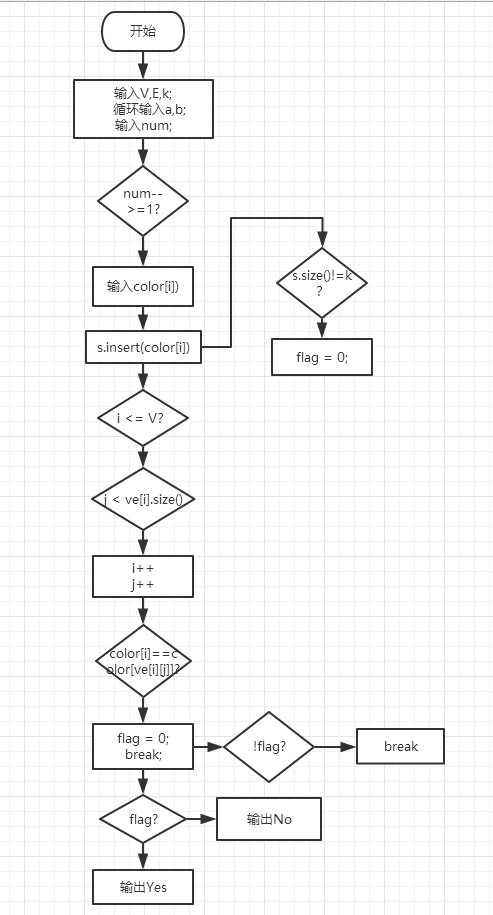
2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

 

2.4 PTA提交列表说明。

这道题中的代码用到了C++的函数，所有编译器应选择C++编译器。还有当s.size()!=k是，标签flag应赋值0。’

2.1 题目2：7-2 排座位

2.2 设计思路（伪代码或流程图）

 

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

 

 

2.4 PTA提交列表说明。

同题目一，应选择C++编译器，还有在combine函数中，a和b的大小关系要讨论以及在不同的分支下应对其采取不同的赋值操作。

2.1 题目3：7-4 公路村村通

2.2 设计思路（伪代码或流程图）

 

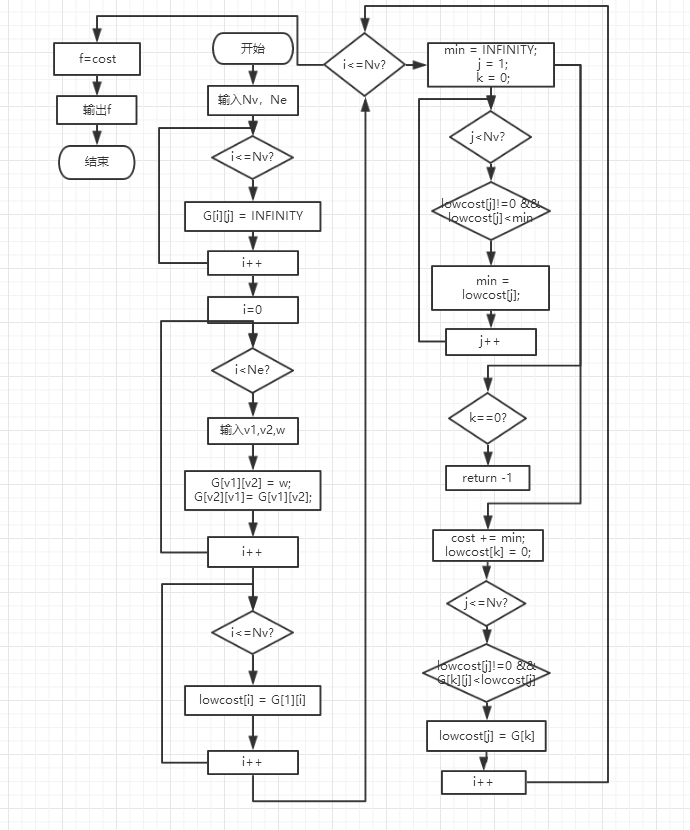
2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

 

 

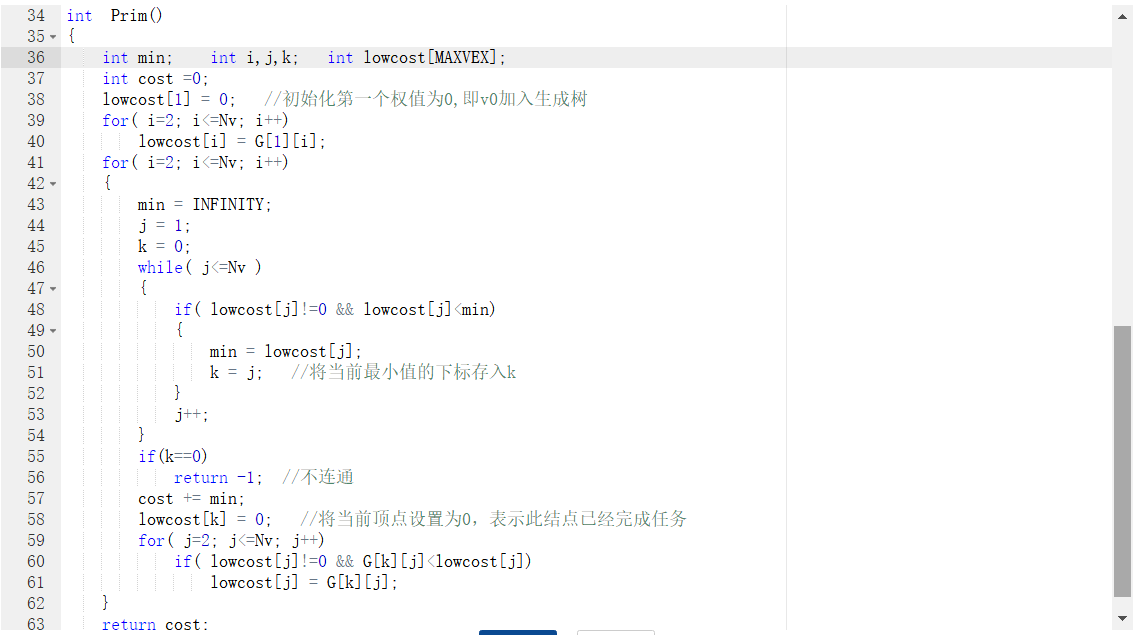
2.4 PTA提交列表说明。

 要注意不连通的情况，以及顶点的设置。

 

3.截图本周题目集的PTA最后排名（3分）

本次题目集总分：310分

3.1 PTA排名（截图带自己名字的排名）

 

3.2 我的总分：180分

本题评分规则：

 （1）PTA总分310分：3分（全部题目都做）
 （2）PTA总分在250分--310分：2.5分（大部分做完1）
 （3）PTA总分在200--250分：2分（大部分做完2）
 （4）PTA总分在150--200分：1.5分
 （5）PTA总分在60分-150分：1分  
 （6）PTA总分在60分以下：0分     

4. 阅读代码（必做，1分）

#include <iostream>
using namespace std;
#define INF 32767
#define MaxVex 20
typedef enum {DG,DN,UDG,UDN}GraphKind;
bool path[MaxVex][MaxVex]={};
bool final[MaxVex];
int D[MaxVex]={0};
int d[MaxVex]={0};
struct ArcCell{
    int adj;
    int *info;
};

struct Graph{
    int vexs[MaxVex];
    ArcCell arcs[MaxVex][MaxVex];
    int vexnum,arcnum;
    GraphKind kind;
};
int getmax(int *d,Graph a)
{
    int result=0;
    for(int i=0;i<a.vexnum;i++)
        if(result<d[i])result=d[i];
    return result;
}
int getmin(int *d,Graph a)
{

    int result=d[0];
    int i,j;
    for(i=0;i<a.vexnum;i++)
        if(result>d[i]){result=d[i];j=i;}
    return j;

}

void input(Graph *graph)
{
    int n;

    cout<<"请输入顶点个数";
    cin>>n;
    graph->vexnum=n;
    cout<<endl<<"请输入无向图的邻接矩阵,无穷时大请输入-1";
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
        {
            cout<<endl<<"arc["<<i<<"]["<<j<<"]=";
            cin>>graph->arcs[i][j].adj;
            if(graph->arcs[i][j].adj==-1)graph->arcs[i][j].adj=INF;
            /*if(i==j){graph->arcs[i][j].adj=0;cout<<endl<<"arc["<<i<<"]["<<j<<"]=0";}
            else if(graph->arcs[j][i].adj>0&&graph->arcs[j][i].adj<=INF){graph->arcs[i][j].adj=graph->arcs[j][i].adj;cout<<endl<<"arc["<<i<<"]["<<j<<"]="<<graph->arcs[j][i].adj;}
            else {cout<<endl<<"arc["<<i<<"]["<<j<<"]=";cin>>graph->arcs[i][j].adj;}
            if(graph->arcs[i][j].adj==-1)graph->arcs[i][j].adj=INF;
            */

        }

}

void Dijkstra(Graph G,int v0)
{
    int min,v,w;
    for(v=0;v<G.vexnum;++v){
        final[v]=false; D[v]=G.arcs[v0][v].adj;
        for(int w=0;w<G.vexnum;++w) path[v][w]=false;
        if(D[v]<INF){path[v][v0]=true;path[v][v]=true;}
    }//for
    D[v0]=0; final[v0]=true;
    for(int i=1;i<G.vexnum;++i){
        min=INF;
        for(w=0;w<G.vexnum;++w)
            if(!final[w])
                if(D[w]<min){v=w;min=D[w];}
        final[v]=true;
        for(w=0;w<G.vexnum;++w)
            if(
                !final[w]&&(min+G.arcs[v][w].adj<D[w])){
                    D[w]=min+G.arcs[v][w].adj;
                    for(int j=0;j<MaxVex;j++)path[w][j]=path[v][j];
                    path[w][w]=true;
            }//if
    }//for


}//dij

void shortpath(Graph a)
{
    int result;
    for(int i=0;i<a.vexnum;i++)
    {
        Dijkstra(a,i);
        d[i]=getmax(D,a);//D[i]为始点到第i个点的最短路径
        //d[i]为始点为i时到其他各点最短路径中的最长路径；
    }
    result=getmin(d,a);
    Dijkstra(a,result);//getmin(d)为结果，医院位置
    for(int j=0;j<a.vexnum;j++)
    {
    cout<<endl<<"从医院(点"<<result+1<<")到村庄（点"<<j+1<<"）最短距离为"<<D[j]<<"线路为";
    int x=0;
    for(int i=0;i<a.vexnum;i++)
    {
        if(path[j][i]==true)
            {
                x++;
                if(x>1)cout<<"->";
                cout<<i+1;
        }
    }
    }

}
void main()
{
    Graph a;
    input(&a);
    shortpath(a);
}