Matlab实现K-Means聚类算法

      人生如戏！！！！

一、理论准备

      聚类算法，不是分类算法。分类算法是给一个数据，然后判断这个数据属于已分好的类中的具体哪一类。聚类算法是给一大堆原始数据，然后通过算法将其中具有相似特征的数据聚为一类。

      K-Means算法的基本思想是初始随机给定K个簇中心，按照最邻近原则把待分类样本点分到各个簇。然后按平均法重新计算各个簇的质心，从而确定新的簇心。一直迭代，直到簇心的移动距离小于某个给定的值。

      算法大致思路：
      1、从给定样本中任选几个点作为初始中心（我取k=2）
      2、计算其余点分别和初始中心点的距离，跟哪个初始中心近就跟那个中心点归为一类(欧式距离公式)，直到各自为“派别”
      3、在分好类的基础上按平均值的方法重新计算聚类中心点，再重复第二步...以此类推
      4、直到最后算法收敛（可以理解为中心点不再变动）则结束。

      小知识点：

    （1）s=size(A),
         当只有一个输出参数时，返回一个行向量，该行向量的第一个元素时矩阵的行数，第二个元素是矩阵的列数。
   （2）[r,c]=size(A),
         当有两个输出参数时，size函数将矩阵的行数返回到第一个输出变量r，将矩阵的列数返回到第二个输出变量c。
   （3）size(A,n)如果在size函数的输入参数中再添加一项n，并用1或2为n赋值，则 size将返回矩阵的行数或列数。其中r=size(A,1)该语句返回的时矩阵A的行数， c=size(A,2) 该语句返回的时矩阵A的列数。
另外，length()=max(size())。

 

二、算法实现

  1: %K-means算法主程序 

  2: k=4; 

  3: x =[ 1.2126   2.1338   0.5115   0.2044 

  4:   -0.9316   0.7634   0.0125   -0.2752 

  5:   -2.9593   0.1813   -0.8833   0.8505 

  6:   3.1104   -2.5393   -0.0588   0.1808 

  7:   -3.1141   -0.1244   -0.6811   0.9891 

  8:   -3.2008   0.0024   -1.2901   0.9748 

  9:   -1.0777   1.1438   0.1996   0.0139 

 10:   -2.7213   -0.1909   0.1184   0.1013 

 11:   -1.1467   1.3820   0.1427   -0.2239 

 12:   1.1497   1.9414   -0.3035   0.3464 

 13:   2.6993   -2.2556   0.1637   -0.0139 

 14:   -3.0311   0.1417   0.0888   0.1791 

 15:   -2.8403   -0.1809   -0.0965   0.0817 

 16:   1.0118   2.0372   0.1638   -0.0349 

 17:   -0.8968   1.0260   -0.1013   0.2369 

 18:   1.1112   1.8802   -0.0291   -0.1506 

 19:   1.1907   2.2041   -0.1060   0.2167 

 20:   -1.0114   0.8029   -0.1317   0.0153 

 21:   -3.1715   0.1041   -0.3338   0.0321 

 22:   0.9718   1.9634   0.0305   -0.3259 

 23:   -1.0377   0.8889   -0.2834   0.2301 

 24:   -0.8989   1.0185   -0.0289   0.0213 

 25:   -2.9815   -0.4798   0.2245   0.3085 

 26:   -0.8576   0.9231   -0.2752   -0.0091 

 27:   -3.1356   0.0026   -1.2138   0.7733 

 28:   3.4470   -2.2418   0.2014   -0.1556 

 29:   2.9143   -1.7951   0.1992   -0.2146 

 30:   3.4961   -2.4969   -0.0121   0.1315 

 31:   -2.9341   -0.1071   -0.7712   0.8911 

 32:   -2.8105   -0.0884   -0.0287   -0.1279 

 33:   3.1006   -2.0677   -0.2002   -0.1303 

 34:   0.8209   2.1724   0.1548   0.3516 

 35:   -2.8500   0.3196   0.1359   -0.1179 

 36:   -2.8679   0.1365   -0.5702   0.7626 

 37:   -2.8245   -0.1312   0.0881   -0.1305 

 38:   -0.8322   1.3014   -0.3837   0.2400 

 39:   -2.6063   0.1431   0.1880   0.0487 

 40:   -3.1341   -0.0854   -0.0359   -0.2080 

 41:   0.6893   2.0854   -0.3250   -0.1007 

 42:   1.0894   1.7271   -0.0176   0.6553 

 43:   -2.9851   -0.0113   0.0666   -0.0802 

 44:   1.0371   2.2724   0.1044   0.3982 

 45:   -2.8032   -0.2737   -0.7391   1.0277 

 46:   -2.6856   0.0619   -1.1066   1.0485 

 47:   -2.9445   -0.1602   -0.0019   0.0093 

 48:   1.2004   2.1302   -0.1650   0.3413 

 49:   3.2505   -1.9279   0.4462   -0.2405 

 50:   -1.2080   0.8222   0.1671   0.1576 

 51:   -2.8274   0.1515   -0.9636   1.0675 

 52:   2.8190   -1.8626   0.2702   0.0026 

 53:   1.0507   1.7776   -0.1421   0.0999 

 54:   -2.8946   0.1446   -0.1645   0.3071 

 55:   -1.0105   1.0973   0.0241   0.1628 

 56:   -2.9138   -0.3404   0.0627   0.1286 

 57:   -3.0646   -0.0008   0.3819   -0.1541 

 58:   1.2531   1.9830   -0.0774   0.2413 

 59:   1.1486   2.0440   -0.0582   -0.0650 

 60:   -3.1401   -0.1447   -0.6580   0.9562 

 61:   -2.9591   0.1598   -0.6581   1.1937 

 62:   -2.9219   -0.3637   -0.1538   -0.2085 

 63:   2.8948   -2.2745   0.2332   -0.0312 

 64:   -3.2972   -0.0219   -0.0288   -0.1436 

 65:   -1.2737   0.7648   0.0643   0.0858 

 66:   -1.0690   0.8108   -0.2723   0.3231 

 67:   -0.5908   0.7508   -0.5456   0.0190 

 68:   0.5808   2.0573   -0.1658   0.1709 

 69:   2.8227   -2.2461   0.2255   -0.3684 

 70:   0.6174   1.7654   -0.3999   0.4125 

 71:   3.2587   -1.9310   0.2021   0.0800 

 72:   1.0999   1.8852   -0.0475   -0.0585 

 73:   -2.7395   0.2585   -0.8441   0.9987 

 74:   -1.2223   1.0542   -0.2480   -0.2795 

 75:   -2.9212   -0.0605   -0.0259   0.2591 

 76:   3.1598   -2.2631   0.1746   0.1485 

 77:   0.8476   1.8760   -0.2894   -0.0354 

 78:   2.9205   -2.2418   0.4137   -0.2499 

 79:   2.7656   -2.1768   0.0719   -0.1848 

 80:   -0.8698   1.0249   -0.2084   -0.0008 

 81:   -1.1444   0.7787   -0.4958   0.3676 

 82:   -1.0711   1.0450   -0.0477   -0.4030 

 83:   0.5350   1.8110   -0.0377   0.1622 

 84:   0.9076   1.8845   -0.1121   0.5700 

 85:   -2.7887   -0.2119   0.0566   0.0120 

 86:   -1.2567   0.9274   0.1104   0.1581 

 87:   -2.9946   -0.2086   -0.8169   0.6662 

 88:   1.0536   1.9818   -0.0631   0.2581 

 89:   -2.8465   -0.2222   0.2745   0.1997 

 90:   -2.8516   0.1649   -0.7566   0.8616 

 91:   -3.2470   0.0770   0.1173   -0.1092 

 92:   -2.9322   -0.0631   -0.0062   -0.0511 

 93:   -2.7919   0.0438   -0.1935   -0.5023 

 94:   0.9894   1.9475   -0.0146   -0.0390 

 95:   -2.9659   -0.1300   0.1144   0.3410 

 96:   -2.7322   -0.0427   -1.0758   0.9718 

 97:   -1.4852   0.8592   -0.0503   -0.1373 

 98:   2.8845   -2.1465   -0.0533   -0.1044 

 99:   -3.1470   0.0536   0.1073   0.3323 

100:   2.9423   -2.1572   0.0505   0.1180 

101:   -3.0683   0.3434   -0.6563   0.8960 

102:   1.3215   2.0951   -0.1557   0.3994 

103:   -0.7681   1.2075   -0.2781   0.2372 

104:   -0.6964   1.2360   -0.3342   0.1662 

105:   -0.6382   0.8204   -0.2587   0.3344 

106:   -3.0233   -0.1496   -0.2607   -0.0400 

107:   -0.8952   0.9872   0.0019   0.3138 

108:   -0.8172   0.6814   -0.0691   0.1009 

109:   -3.3032   0.0571   -0.0243   -0.1405 

110:   0.7810   1.9013   -0.3996   0.7374 

111:   -0.9030   0.8646   -0.1498   0.1112 

112:   -0.8461   0.9261   -0.1295   -0.0727 

113:   2.8182   -2.0818   -0.1430   -0.0547 

114:   2.9295   -2.3846   -0.0244   -0.1400 

115:   1.0587   2.2227   -0.1250   0.0957 

116:   3.0755   -1.7365   -0.0511   0.1500 

117:   -1.3076   0.8791   -0.3720   0.0331 

118:   -2.8252   -0.0366   -0.6790   0.7374 

119:   -2.6551   -0.1875   0.3222   0.0483 

120:   -2.9659   -0.1585   0.4013   -0.1402 

121:   -3.2859   -0.1546   0.0104   -0.1781 

122:   -0.6679   1.1999   0.1396   -0.3195 

123:   -1.0205   1.2226   0.1850   0.0050 

124:   -3.0091   -0.0186   -0.9111   0.9663 

125:   -3.0339   0.1377   -0.9662   1.0664 

126:   0.8952   1.9594   -0.3221   0.3579 

127:   -2.8481   0.1963   -0.1428   0.0382 

128:   1.0796   2.1353   -0.0792   0.6491 

129:   -0.8732   0.8985   -0.0049   0.0068 

130:   1.0620   2.1478   -0.1275   0.3553 

131:   3.4509   -1.9975   0.1285   -0.1575 

132:   -3.2280   -0.0640   -1.1513   0.8235 

133:   -0.6654   0.9402   0.0577   -0.0175 

134:   -3.2100   0.2762   -0.1053   0.0626 

135:   3.0793   -2.0043   0.2948   0.0411 

136:   1.3596   1.9481   -0.0167   0.3958 

137:   -3.1267   0.1801   0.2228   0.1179 

138:   -0.7979   0.9892   -0.2673   0.4734 

139:   2.5580   -1.7623   -0.1049   -0.0521 

140:   -0.9172   1.0621   -0.0826   0.1501 

141:   -0.7817   1.1658   0.1922   0.0803 

142:   3.1747   -2.1442   0.1472   -0.3411 

143:   2.8476   -1.8056   -0.0680   0.1536 

144:   -0.6175   1.4349   -0.1970   -0.1085 

145:   0.7308   1.9656   0.2602   0.2801 

146:   -1.0310   1.0553   -0.2928   -0.1647 

147:   -2.9251   -0.2095   0.0582   -0.1813 

148:   -0.9827   1.2720   -0.2225   0.2563 

149:   -1.0830   1.1158   -0.0405   -0.1181 

150:   -2.8744   0.0195   -0.3811   0.1455 

151:   3.1663   -1.9241   0.0455   0.1684 

152:   -1.0734   0.7681   -0.4725   -0.1976]; 

153: [n,d] = size(x); 

154: bn=round(n/k*rand);%第一个随机数在前1/K的范围内 

155: %；表示按列显示，都好表示按行显示

156: nc=[x(bn,:);x(2*bn,:);x(3*bn,:);x(4*bn,:)];%初始聚类中心 

157: %x(bn,:) 选择某一行数据作为聚类中心，其列值为全部

158: 

159: %x数据源，k聚类数目，nc表示k个初始化聚类中心

160: %cid表示每个数据属于哪一类，nr表示每一类的个数，centers表示聚类中心

161: [cid,nr,centers] = kmeans(x,k,nc)%调用kmeans函数 

162: %认为不该是150，或者说不该是个确定值，该是size(x,1)就是x行数

163: for i=1:150

164:   if cid(i)==1, 

165:      plot(x(i,1),x(i,2),'r*') % 显示第一类

166:     %plot(x(i,2),'r*') % 显示第一类

167:     hold on 

168:   else 

169:       if cid(i)==2, 

170:         plot(x(i,1),x(i,2),'b*') %显示第二类 

171:         %  plot(x(i,2),'b*') % 显示第一类

172:           hold on 

173:       else 

174:               if cid(i)==3, 

175:                     plot(x(i,1),x(i,2),'g*') %显示第三类 

176:                    % plot(x(i,2),'g*') % 显示第一类

177:                     hold on 

178:                   else 

179:                       if cid(i)==4, 

180:                        plot(x(i,1),x(i,2),'k*') %显示第四类

181:                         % plot(x(i,2),'k*') % 显示第一类

182:                         hold on 

183:                       end 

184:               end 

185:         end 

186:   end 

187: end 

188: strt=['红色*为第一类；蓝色*为第二类；绿色*为第三类；黑色*为第四类' ]; 

189: text(-4,-3.6,strt); 

 

  1: %BasicKMeans.m主类 

  2: %x数据源，k聚类数目，nc表示k个初始化聚类中心

  3: %cid表示每个数据属于哪一类，nr表示每一类的个数，centers表示聚类中心

  4: function [cid,nr,centers] = kmeans(x,k,nc) 

  5:     [n,d] = size(x); 

  6:     % 设置cid为分类结果显示矩阵 

  7:     cid = zeros(1,n); 

  8:     % Make this different to get the loop started. 

  9:     oldcid = ones(1,n); 

 10:     % The number in each cluster. 

 11:     nr = zeros(1,k); 

 12:     % Set up maximum number of iterations. 

 13:     maxgn= 100; 

 14:     iter = 1; 

 15:     %计算每个数据到聚类中心的距离 ,选择最小的值得位置到cid

 16:     %我记得是聚类中心近乎不再变化迭代停止

 17:     while iter < maxgn  

 18:         for i = 1:n 

 19:             %repmat 即 Replicate Matrix ，复制和平铺矩阵，是 MATLAB 里面的一个函数。

 20:             %B = repmat(A,m,n)将矩阵 A 复制 m×n 块，即把 A 作为 B 的元素，B 由 m×n 个 A 平铺而成。B 的维数是 [size(A,1)*m, size(A,2)*n] 。

 21:             %点乘方a.^b,矩阵a中每个元素按b中对应元素乘方或者b是常数

 22:             %sum(x,2)表示矩阵x的横向相加，求每行的和，结果是列向量。 而缺省的sum(x)就是竖向相加，求每列的和，结果是行向量。

 23:             dist = sum((repmat(x(i,:),k,1)-nc).^2,2); 

 24:             [m,ind] = min(dist); % 将当前聚类结果存入cid中 

 25:             cid(i) = ind; 

 26:         end 

 27:          %找到每一类的所有数据，计算他们的平均值，作为下次计算的聚类中心 

 28:         for i = 1:k 

 29:             %find（A>m,4）返回矩阵A中前四个数值大于m的元素所在位置

 30:             ind = find(cid==i); 

 31:             %mean(a,1)=mean(a)纵向;mean(a,2)横向

 32:             nc(i,:) = mean(x(ind,:)); 

 33:             %统计每一类的数据个数 

 34:             nr(i) = length(ind); 

 35:         end 

 36:         iter = iter + 1; 

 37:     end 

 38: 

 39:     % Now check each observation to see if the error can be minimized some more. 

 40:     % Loop through all points. 

 41:     

 42:     maxiter = 2;

 43:     iter = 1; 

 44:     move = 1; 

 45:     %j~=k这是一个逻辑表达式，j不等于k，如果j不等于k，返回值为1，否则为0

 46:     while iter < maxiter & move ~= 0 

 47:         move = 0; 

 48:         %对所有的数据进行再次判断，寻求最佳聚类结果 

 49:         for i = 1:n 

 50:             dist = sum((repmat(x(i,:),k,1)-nc).^2,2); 

 51:             r = cid(i); % 将当前数据属于的类给r 

 52:             %点除，a.\b表示矩阵b的每个元素除以a中对应元素或者除以常数a，a./b表示常数a除以矩阵b中每个元素或者矩阵a除以矩阵b对应元素或者常数b

 53:             %nr是没一类的的个数

 54:             

 55:             

 56:             

 57:             %这个调整看不懂

 58:             %点乘(对应元素相乘),必须同维或者其中一个是标量，a.*b

 59:             dadj = nr./(nr+1).*dist'; % 计算调整后的距离 

 60:             

 61:             [m,ind] = min(dadj); % 找到该数据距哪个聚类中心最近 

 62:             if ind ~= r % 如果不等则聚类中心移动 

 63:                   cid(i) = ind;%将新的聚类结果送给cid 

 64:                   ic = find(cid == ind);%重新计算调整当前类别的聚类中心 

 65:                   nc(ind,:) = mean(x(ic,:)); 

 66:                   move = 1; 

 67:             end 

 68:         end 

 69:         iter = iter+1; 

 70:     end 

 71:     centers = nc; 

 72:     if move == 0 

 73:         disp('No points were moved after the initial clustering procedure.') 

 74:     else 

 75:         disp('Some points were moved after the initial clustering procedure.') 

 76:     end

 

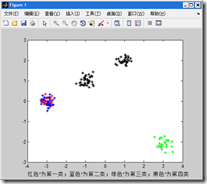
三、算法结果

      控制台自动输出的结果如下，我很奇怪怎么自己输出了。

  1: >> main

  2: No points were moved after the initial clustering procedure.

  3: cid =

  4:   Columns 1 through 22

  5:      2     3     1     4     1     1     3     1     3     2     4     1     1     2     3     2     2     3     1     2     3     3

  6:   Columns 23 through 44

  7:      1     3     1     4     4     4     1     1     4     2     1     1     1     3     1     1     2     2     1     2     1     1

  8:   Columns 45 through 66

  9:      1     2     4     3     1     4     2     1     3     1     1     2     2     1     1     1     4     1     3     3     3     2

 10:   Columns 67 through 88

 11:      4     2     4     2     1     3     1     4     2     4     4     3     3     3     2     2     1     3     1     2     1     1

 12:   Columns 89 through 110

 13:      1     1     1     2     1     1     3     4     1     4     1     2     3     3     3     1     3     3     1     2     3     3

 14:   Columns 111 through 132

 15:      4     4     2     4     3     1     1     1     1     3     3     1     1     2     1     2     3     2     4     1     3     1

 16:   Columns 133 through 150

 17:      4     2     1     3     4     3     3     4     4     3     2     3     1     3     3     1     4     3

 18: nr =

 19:     55    30    40    25

 20: centers =

 21:   -2.962918181818183  -0.023009090909091  -0.297021818181818   0.341136363636364

 22:    0.995233333333333   1.997873333333334  -0.078486666666667   0.229650000000000

 23:   -0.956882500000000   0.997800000000000  -0.123667500000000   0.049320000000000

 24:    3.023444000000000  -2.098592000000001   0.102096000000000  -0.050580000000000

      每次运行结果得到的图片都不一样，最奇怪的是第二个图片竟然重叠类别。

                

四、结果分析

      不适合处理离散型属性，但是对于连续型具有较好的聚类效果。

      对于不同的初始值，可能会导致不同结果：多设置一些不同的初值，但比较耗时和浪费资源。

      分类数目K不确定：通过类的自动合并和分裂，得到较为合理的类型数目K，例如ISODATA算法。相同点：聚类中心都是通过样本均值的迭代运算来决定的；不同点：主要是在选代过程中可将一类一分为二，亦可能二类合二为一，即“自组织”，这种算法具有启发式的特点。由于算法有自我调整的能力，因而需要设置若干个控制用参数，如聚类数期望值K、最小类内样本数、类间中心距离参数、每次迭代允许合并的最大聚类对数L及允许迭代次数I等。

      参考了老王的课件。