编程之美:平面最近点对
一.概念引入
最接近点对问题的提法是:给定平面上n个点,找其中的一对点,使得在n个点的所有点对中,该点对的距离最小。严格地说,最接近点对可能多于1对。为了简单起见,这里只限于找其中的一对。
最简单的就是直接暴力,也可以分治,使用分治的话关键是如何合并,如果两边都是n/2个点比较的话,合并的时间是O(n^2),那么T(n)=2T(n/2)+O(n2),它的解为T(n)=O(n2),还是没什么优势,这就引导我们去优化合并算法。
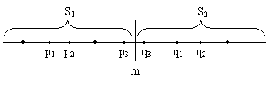
为了找到一个有效的合并算法,可以先考虑一维情形,看下图:
假设左右两边的最小距离是ans={ans1,ans2},很有可能最小距离分别存在于直线两端p3、q3,如果真是这样,则一定在p3∈(m-δ,m],q3∈(m,m+δ],且根据鸽巢原理,在这两个半闭区间只有一个点,否则就违背了ans的定义(两边存在更小距离),关键是选好划分点,最坏T(n)=T(n-1)+O(n),它的解是T(n)=O(n2),这种效率降低的现象可以通过适当选择分割点m,使左右两边有大致相等个数的点。
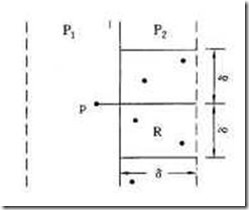
下面看二维情形:
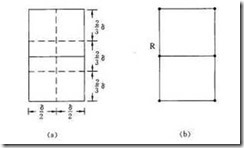
考虑P1中任意一点p,它若与P2中的点q构成最接近点对的候选者,则必有dis(p,q)<ans(图中的sigma)。满足这个条件的P2中的点有多少个呢?容易看出这样的点一定落在一个δ×2δ的矩形R中,由δ的意义可知P2中任何2个S中的点的距离都不小于δ。由此可以推出矩形R中最多只有6个S中的点。事实上,我们可以将矩形R的长为2δ的边3等分,将它的长为δ的边2等分,由此导出6个(δ/2)×(2δ/3)的矩形,如下图
若矩形R中有多于6个S中的点,则由鸽舍原理易知至少有一个δ×2δ的小矩形中有2个以上S中的点。设u,v是这样2个点,它们位于同一小矩形中,则因此d(u,v)≤5δ/6<δ 。这与δ的意义相矛盾。也就是说矩形R中最多只有6个S中的点。图4(b)是矩形R中含有S中的6个点的极端情形。由于这种稀疏性质,对于P1中任一点p,P2中最多只有6个点与它构成最接近点对的候选者。因此,在分治法的合并步骤中,我们最多只需要检查6×n/2=3n对候选者,而不是n2/4对候选者。这是否就意味着我们可以在O(n)时间内完成分治法的合并步骤呢?现在还不能作出这个结论,因为我们只知道对于P1中每个S1中的点p最多只需要检查P2中的6个点,但是我们并不确切地知道要检查哪6个点。为了解决这个问题,我们可以将p和P2中所有S2的点投影到垂直线l上。由于能与p点一起构成最接近点对候选者的S2中点一定在矩形R中,所以它们在直线l上的投影点距p在l上投影点的距离小于δ。由上面的分析可知,这种投影点最多只有6个。因此,若将P1和P2中所有S的点按其y坐标排好序,则对P1中所有点p,对排好序的点列作一次扫描,就可以找出所有最接近点对的候选者,对P1中每一点最多只要检查P2中排好序的相继6个点。
参考资料:http://blog.csdn.net/junerfsoft/article/details/2975495
二.算法Java实现
以hdu1007为例,果断AC……
import java.util.*; /* * x轴排序tle,y轴果断ac */ public class HDU1007 { public static void main(String[] args) { new DK().go(); } } class Point implements Comparable<Point>{ double x; double y; public Point() { this.x = 0; this.y = 0; } @Override public int compareTo(Point obj) { Point other = obj; if(this.y!=other.y) {//由小到大排序 return (int)Math.ceil(this.y - other.y); } return (int)Math.ceil(this.x - other.x); } } class DK { double x; double y; Point point[]; int a[]; public void go() { Scanner sc = new Scanner(System.in); while(true) { int n = sc.nextInt(); if(0==n) { break; } point = new Point[n]; for(int i=0; i<n; i++) { point[i] = new Point(); } for(int i=0; i<n; i++) { x = sc.nextDouble(); y = sc.nextDouble(); point[i].x = x; point[i].y = y; } Arrays.sort(point); // for(int i=0; i<n; i++) { // System.out.println(point[i].x+" "+point[i].y); // } a = new int[n]; double ans = solve(0,n-1)/2; System.out.println(String.format("%.2f", ans)); } } private double solve(int left, int right) { double ans = 1e-7; if(left==right) { return ans; } if(left==right-1) { return distance(point[left], point[right]); } int mid = (left+right)>>1; double ans1 = solve(left,mid); //注意:不是mid+1 double ans2 = solve(mid,right); ans = Math.min(ans1,ans2); int j = 0; for(int i=left; i<=right; i++) { if(Math.abs(point[i].y-point[mid].y)<=ans) { a[j++] = i; } } /* * 加上下面的排序就AC,否则WA,我认为至多TLE, * 因为扫描的是和point[i]最相近的两个矩形2*ans区间 */ //不知道如何用comparator接口实现间接排序,所以就写了个选择排序 mySort(a,j); for(int i=0; i<j; i++) { for(int k=i+1; k<j&&Math.abs(point[a[i]].x - point[a[k]].x)<ans; k++) { double dis = distance(a[i], a[k]); if(ans>dis) { ans = dis; } } } return ans; } private void mySort(int[] a, int j) { for(int i=0; i<j; i++) { for(int k=i+1; k<j; k++) { if(point[a[i]].x<point[a[k]].x) { int temp = a[i]; a[i] = a[k]; a[k] = temp; } } } } private double distance(Point p1, Point p2) { double dis = Math.hypot(p1.x-p2.x, p1.y-p2.y); return dis; } private double distance(int i, int j) {//point搞为成员变量 double dis = Math.hypot(point[i].x-point[j].x, point[i].y-point[j].y); return dis; } } //class Com implements Comparator<Point> { // // @Override // public int compare(Point o1, Point o2) { // // return o1.y - o2.y; // } //}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号