习题汇总

习题2.65

当x有偶数个1时输出1，否则输出0。

代码：

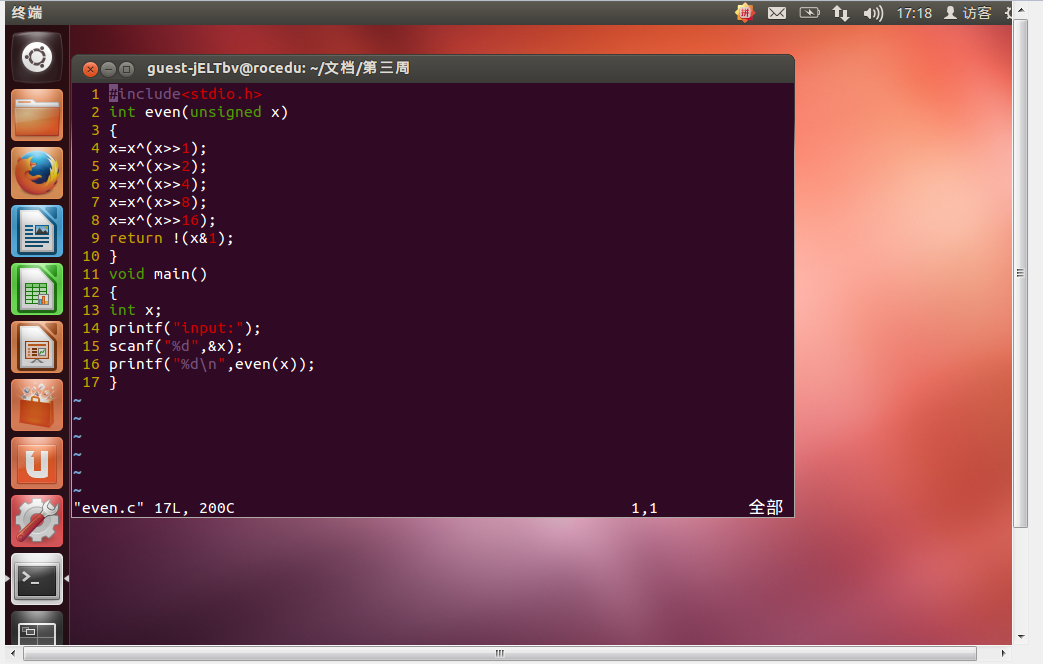
 测试数据：

0=00000000

3=00000011

167=10100111

243=11110011

原理：

在假设int有32位的情况下，第一次异或的结果得出每两位1的个数的奇偶性，以末两位为例，若末两位为偶数个1，则得数最后一位为0，以此类推；

同理第二次异或得出每四位1的个数的奇偶性，以末四位为例，若末四位为偶数个1，则得数最后一位为0，以此类推；

......

五次异或后，最后一位得出所有32位的1的奇偶性，若有偶数个1，最后一位为0，否则为1，将得数与1异或为返回值。

 

 

 

习题3.66

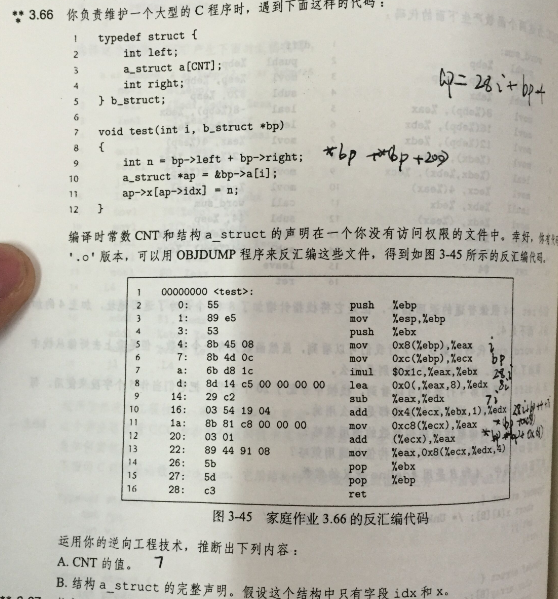
由题假设： CNT=A；

struct a_struct{

int idx;

int x[B];

}

 

c代码可得：

n=*bp+*(bp+4+4A(B+1))

ap=bp+4+4(B+1)i

ap->idx=*(bp+4+4(B+1)i)

ap->x[ap->idx]=bp+4+4(B+1)i+4+4·*(bp+4+4(B+1)i)=n

 

另反汇编代码可得：

5   i->eax

6   bp->ecx

7   28i->ebx

8   8i->edx

9   7i->edx

10  *(28i+bp+4)+7i->edx

11  *(bp+200)->eax

12  *bp+*(bp+200) ->eax

13  eax->*(edx·4+bp+8)

 

可轻易看出反汇编代码12行对应c代码第9行，反汇编代码13行对应c代码11行。

 

故综上可得：

4A(B+1)+4=200且4(B+1)=28

故A=7,B=6。