从优化的角度谈谈排序
1.插入排序
插入排序其实就是把n个待排序的元素看成为一个有序表和一个无序表。开始时有序表中只包含1个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,将它插入到有序表中的适当位置,使之成为新的有序表,重复n-1次可完成排序过程。
下面选取直接插入排序的一个中间过程对其进行说明。假设{20,30,40,10,60,50}中的前3个数已经排列过,是有序的了;接下来对10进行排列。示意图如下:

Java实现:
public static void insertsort(int arr[],int n){ for(int i=1;i<n;i++){ for(int j=i;j>0;j--){ if(arr[j]>arr[j-1]){ int temp=arr[j]; arr[j]=arr[j-1]; arr[j-1]=temp; } else{ return; } } } }
如果我们写成这样,还有优化的必要吗?
有,忽略交换的时间,从时间复杂度来看这是一个O(n^2)算法,这个算法在数组小的时候还行,但是多的话,交换的时间明显拉长了插入排序的时间。来看看下面这个:
public static void insertSort(int arr[],int r){ int i,j,tmp; for (i = 1; i < r; i++) { tmp = arr[i]; for (j = i - 1; j >= 0 && arr[j] > tmp; j--) { arr[j+1] = arr[j]; } arr[j+1] = tmp; } }
优化在那里了,以赋值代替了交换。
2.快速排序
它的基本思想是:选择一个基准数,通过一趟排序将要排序的数据分割成独立的两部分;其中一部分的所有数据都比另外一部分的所有数据都要小。然后,再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
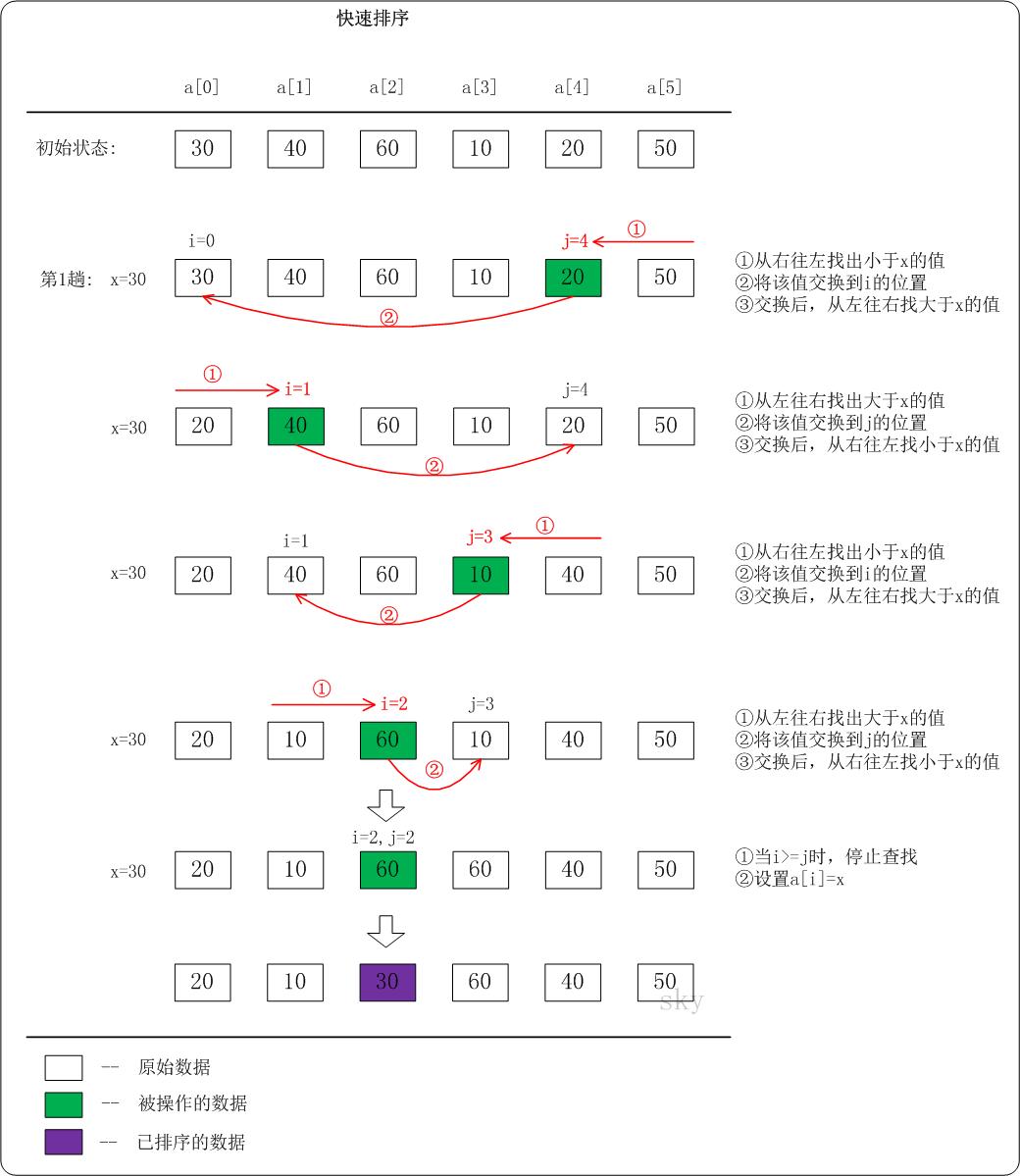
下面以数列a={30,40,60,10,20,50}为例,演示它的快速排序过程(如下图)。
上图演示的是两路快速排序,思想也简单,左右查找,左右交换.。
Java实现:
public static void quicksort(int arr[],int l,int r){ if(l<r) { int i, j, x; i = l; j = r; x = arr[i]; while (i < j) { //为什么还要判断i<j呢? //防止while判断越界 while (i < j && arr[j] > x) { j--;//从右往左寻找大于x的值 } if (i < j) { //将这个小于x的值赋值给arr[i],i++ arr[i++] = arr[j]; } while (i < j && arr[i] < x) { i++;//从左从有寻找小于x的值 } if (i < j) { //将这个大于x的值赋值给arr[j],j-- arr[j--] = arr[i]; } } //将x放到合适的位置 arr[i] = x; //开始递归 quicksort(arr, l, i - 1); quicksort(arr, i + 1, r); } else{ return; } }
a.我们想一想,快速排序的思想是选定第一个数为基准,如果数组是这样{60,50,40,30,20,10},目标是从小到大排序,这样的话,数组遍历的深度就是N了,时间复杂度就成了O(n^2),有没有一种办法减缓这种情况,答案是有:
public static void quicksort(int arr[],int l,int r){ if(l<r) { Random rand = new Random(); int i, j, x; i = l; j = r; int random = rand.nextInt(j - i + 1) + i; swap(arr,i,random); x = arr[i]; while (i < j) { //为什么还要判断i<j呢? //防止while判断越界 while (i < j && arr[j] > x) { j--;//从右往左寻找大于x的值 } if (i < j) { //将这个小于x的值赋值给arr[i],i++ arr[i++] = arr[j]; } while (i < j && arr[i] < x) { i++;//从左从有寻找小于x的值 } if (i < j) { //将这个大于x的值赋值给arr[j],j-- arr[j--] = arr[i]; } } //将x放到合适的位置 arr[i] = x; //开始递归 quicksort(arr, l, i - 1); quicksort(arr, i + 1, r); } else{ return; } }
public static void swap(int a[],int i,int j){ int m; m=a[i]; a[i]=a[j]; a[j]=m; }
先说说为什么swap()写的这么别扭,为什么不直接写成这样:
public static void swap(int i,int j){ int m; m=i; i=j; j=m; }
这是因为Java中值传递和引用传递的问题。
在说说这种优化,随机选择一个基准数,这种优化可以说是在某种程度有作用。
b.如果碰到有很多重复元素,我们还要以上面的实现思路去实现他吗?我们可不可以遇到重复的元素就把它一次性放到它最终的位置,这样速度会提高很多。
public static void quick3sort(int arr[],int l,int r){ if(l<r){ //lt记录小于x的值的位置 //rt纪录大于x的值 //i记录排序的地点 int lt,rt,i,x; lt=l; rt=r; i=l+1; x=arr[lt]; while(lt<rt){ if(arr[i]<x){ swap(arr,i,rt); i++; lt++; } else if(arr[i]>x){ swap(arr,i,rt); rt--; } else{ i++; } } swap(arr,lt,x); //开始递归 quicksort(arr, l, lt-1); quicksort(arr, rt, r); } }
swap方法上面提到过了,就不贴出来了。
c.还有没有优化的地方呢?
有,看看下面:
public static void quicksort(int arr[],int l,int r){ if(l-r>5) { int i, j, x; i = l; j = r; x = arr[i]; while (i < j) { //为什么还要判断i<j呢? //防止while判断越界 while (i < j && arr[j] > x) { j--;//从右往左寻找大于x的值 } if (i < j) { //将这个小于x的值赋值给arr[i],i++ arr[i++] = arr[j]; } while (i < j && arr[i] < x) { i++;//从左从有寻找小于x的值 } if (i < j) { //将这个大于x的值赋值给arr[j],j-- arr[j--] = arr[i]; } } //将x放到合适的位置 arr[i] = x; //开始递归 quicksort(arr, l, i - 1); quicksort(arr, i + 1, r); } else{ //可以使用插入排序 } }
这种优化就需要我们去探索了,当l-r>n(n为多少的时候,算法是最优的),我们都知道在数组接近有序的情况下,时间复杂度是O(n),观察到快速排序排到最后的时候数组接近有序,所以算法之间的组合岂不是更妙!
3.归并排序
将两个的有序数列合并成一个有序数列,我们称之为"归并"。

① 分解 -- 将当前区间一分为二,即求分裂点 mid = (low + high)/2。
② 求解 -- 递归地对两个子区间a[low...mid] 和 a[mid+1...high]进行归并排序。递归的终结条件是子区间长度为1。
③ 合并 -- 将已排序的两个子区间a[low...mid]和 a[mid+1...high]归并为一个有序的区间a[low...high]。
Java实现(从上往下):
public static void mergeSort(int arr[],int l,int mid,int r){ //复制一份数组 int arrcopy[]=new int[r-l+1]; //标定零界点 int i=l; int j=mid+1; int k=0; while(i<=mid &&j<=r){ if(arr[i]<=arr[j]){ arrcopy[k++]=arr[i++]; }else{ arrcopy[k++]=arr[j++]; } } //归并排序有可能分的不均等 while(i<=mid){ arrcopy[k++]=arr[i++]; } while(j<=r){ arrcopy[k++]=arr[j++]; } //k=r-1+1-1 for(int m=0;m<k;m++){ arr[l++]=arrcopy[m]; } arrcopy=null; } public static void upTodown(int arr[],int l,int r){ if(l>=r || arr==null){ return; } int mid =(l+r)/2; upTodown(arr,l,mid); upTodown(arr,mid+1,r); //partition mergeSort(arr, l, mid, r); }
归并排序将两个有序数组合并,我们可以这样优化,当使用mergeSort的方法的时候,我们判断一下,这两个有序数组是否已经有序,即判断数组在mid和mid+1的值。
public static void mergeSort(int arr[],int l,int mid,int r){ //复制一份数组 int arrcopy[]=new int[r-l+1]; //标定零界点 int i=l; int j=mid+1; int k=0; while(i<=mid &&j<=r){ if(arr[i]<=arr[j]){ arrcopy[k++]=arr[i++]; }else{ arrcopy[k++]=arr[j++]; } } //归并排序有可能分的不均等 while(i<=mid){ arrcopy[k++]=arr[i++]; } while(j<=r){ arrcopy[k++]=arr[j++]; } //k=r-1+1-1 for(int m=0;m<k;m++){ arr[l++]=arrcopy[m]; } arrcopy=null; } public static void upTodown(int arr[],int l,int r){ if(l>=r || arr==null){ return; } int mid =(l+r)/2; upTodown(arr,l,mid); upTodown(arr,mid+1,r); //优化改动点 if(arr[mid]>arr[mid+1]) { //partition mergeSort(arr, l, mid, r); } }
当然归并排到最后也会出现数组基本有序的情况,所以我们可以参考上面,当l-r>n(n为某个值)的时候改用插入排序,归并排序无法进步到O(n)的程度的,所以还是有优化的空间的。
优化就看到这,以后有想法会更新。
博客不易,转载请注明地址:http://www.cnblogs.com/huhu1203/p/7725948.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号