软件工程实践2017第二次作业
github项目地址
注意是master分支
解题思路描述:
在刚拿到题目的时候,我有以下几种想法:
1.以行为角度,生成第一行,形成约束条件再生成第二行,再生成约束条件生成第三行但是在实际操作的过程中,生成的难度很大,因为既要满足行出现一次,列出现一次,但 是又要在一块中满足1~9都出现一次.
2.以块为角度,生成第一块,再生成第二块和第四块,再生成第三五七块~~~总体而言就是从左上角向右下角构造,但是在操作过程中,将一个块用一个一维数组表示,最终跟想法一其实是一样的,一个行是一个19随意排列的数组,一个块也是19随意排列的数组
3.以格为角度.这道数独问题和以前接触的八皇后问题有一点共同点:行列不冲突.所以就想到了十字法.定下一个数字,行列该数字不在出现.且前三行为例,若第一块的1在第一行,则说明第二块和第三块的1要占据第二或第三行,总共有33+33中情况.以此类推.
可是这么多想法,该选定哪一种呢?每一种都尝试过了,体会就是思路不清,像陷入了代码的泥潭中,像一团乱麻,对每一行的处理很难找出共性用一些简洁的函数去表达。在生成行或者块的过程中各种约束让人无法展开拳脚。

于是就决定上网看看。在网上搜索资料的过程中,发现了网友们的几种思路:
1.矩阵变换法:根据一个原始数独矩阵进行变换(如交换行,列,对应数字,旋转等)得到新数独矩阵,可是根据原始矩阵进行变换得出的结果数量可能达不到题目的要求,故放弃该思路.
2.随机法:其根据终盘数量极大来假设:按照这个数量,如果我们将一个[1,2,3,4,5,6,7,8,9]的数组随机化,然后将其作为一行数据添加到一个二维数组中去,该行能满足数独终盘规则的概率是很大的。但是随机法的控制成了难题。题干要求不重复的,但是随机法是存在重复可能。故放弃该思路。
参考网址:
数独终盘生成的几种方法
Swing数独游戏(一):终盘生成之矩阵转换法
Swing数独游戏(二):终盘生成之随机法
在网上浏览没有看到结果后,就决定继续按照之前的思路待在泥潭里。
到了晚上,跟人交流的过程中,有人问我:“你有试过暴力深搜吗”。
说实在的,之前有想过一丝念头,但是很快就泯灭了,因为题目对性能有要求的。个人对于深搜之类的算法是心有芥蒂的,对于暴力也是抗拒的,从小到大老师都在教导我们尽量一题多解且以巧解为妙。但是在这种情况下不妨一试。
深搜的优点就是思路清晰,可读性强。
设计实现过程:
一开始以行或者块作为对象的时候,代码主要有以下几个类:
主程序
数独类
行或者块类(后来发现可以用一个一维数组表示,就删去了)
工具类
后来改为DFS方法之后:
主程序
数独类
工具类
类之间的关系是:
主程序调用数独类的启动函数,工具类实现读取参数和打印数独的作用

代码说明
Sudoku类中的dfs和check函数最为核心
private void dfs(int x, int y)
{
for (int i = 1; i < 10; i++)
{
//到达规定数目,文件指针关闭
if (Util.Count == max)
{
return;
}
if (check(i, x, y))
{
sudoku[x, y] = i;
//到头打印
if (x == 9 && y == 9)
{
Util.Show(ref sudoku);
return;
}
//换行深搜
else if (y == 9) dfs(x + 1, 1);
else dfs(x, y + 1);
}
}
return;
}
private Boolean check(int i, int x, int y)
{
//行检查
for (int k = 1; k < y; k++)
{ if (sudoku[x, k] == i) return false; }
//列检查
for (int k = 1; k < x; k++)
{ if (sudoku[k, y] == i) return false; }
//九宫格检查
//找到每个块的起始点
int a = (x - 1) / 3 * 3 + 1;
int b = (y - 1) / 3 * 3 + 1;
int j_max = a + 3;
int k_max = b + 3;
//改进,同行同列不检查
for (int j = a; j < j_max; j++)
{
if (j == x) {
continue;
}
for (int k = b; k < k_max; k++)
{
if (k == y)
{
continue;
}
if (sudoku[j, k] == i)
{
return false;
}
}
}
return true;
}
测试运行

单元测试

代码覆盖率
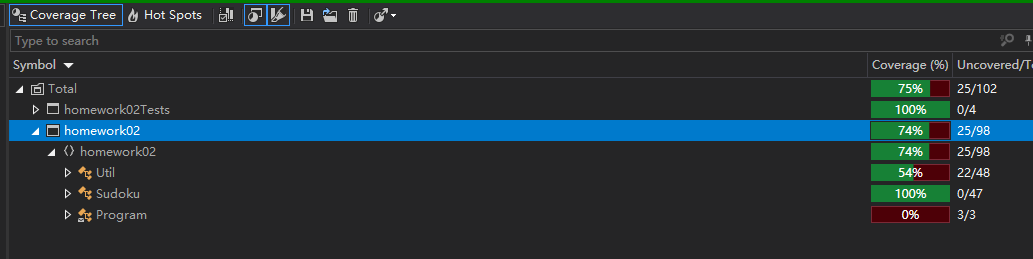
效能分析与改进:
N=1000000
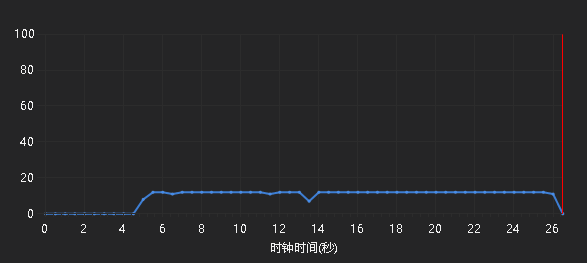


运行约22s
对于[mscrolib.ni.dll]网上搜不出什么资料,只找到了mscrolib.dll
改进思路:部分已在贴出的源码中体现
改进的思路有两条,一个是在check中做文章,另一个则是在IO中。
1.check函数中减少不必要的检查
改进了一些我所能想到的。
2.文件输出中采用多线程
在学习操作系统这门课时知道了IO操作是很耗时的,在改进的时候想过要多线程,但是发现不可行,原因如下:
1.输出打印的数组如果不进行复制,就会导致输出结果不正确(如果把数组编程同步变量消耗会很大)。如果进行复制,就会导致多次GC,更加影响性能。
2.锁变量是输出流,但是输出的结果跟是否是头一个有关,所以输出函数的参数有数组array和输出个数count,而c#对于多个参数的函数进行线程调用很复杂,需要将参数写成一个object列表进行传递(类型转换开销),或者将参数写成一个类传递(损失代码可读性)
所以放弃了多线程思路
ps:
在dev分支中将Util类的函数进一步抽象化,提高代码复用,但是影响些许性能。
另外如果将所有功能尽可能写在少许的函数中减少函数调用的开销,性能会提高许多(我试过),但是代码的可读性降低,复用性不强。
PSP 2.1表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 30 |
| · Estimate | · 估计这个任务需要多少时间 | 30 | 30 |
| Development | 开发 | 630 | 690 |
| · Analysis | · 需求分析 (包括学习新技术) | 300 | 360 |
| · Design Spec | · 生成设计文档 | 30 | 30 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 0(没有同事) | 0 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 0(交给编译器了) | 0 |
| · Design | · 具体设计 | 60 | 60 |
| · Coding | · 具体编码 | 120 | 120 |
| · Code Review | · 代码复审 | 60 | 60 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 60 |
| Reporting | 报告 | 120 | 60 |
| · Test Report | · 测试报告 | 60 | 30 |
| · Size Measurement | · 计算工作量 | 30 | 30 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 60 |
| 合计 | 780 | 780 |
ps:有些时间的分类不知道属于什么部分,比如在思考--实践--重做这样的循环中。另外有些时间的分类比较混杂,因为有些事糅合在一起做了。





