Scipy Lecture Notes学习笔记(一)Getting started with Python for science 1.3. NumPy: creating and manipulating numerical data
-
1.3. NumPy: creating and manipulating numerical data
创建和操作数值数据
摘要:
-
了解如何创建数组:
array,arange,ones,zeros。 -
了解数组的形状
array.shape,然后使用切片来获得数组的不同视图:array[::2]等等。使用reshape或调平数组的形状来调整数组的形状ravel。 -
获取数组元素的子集和/或用掩码修改它们的值
>>> a [ a < 0 ] = 0 -
知道数组上的其他操作,例如查找平均值或最大值(
array.max(),array.mean())。没有必要保留所有内容,但需要在文档中进行搜索(在线文档help(),,lookfor())! -
高级用途:掌握整数数组的索引,以及广播。知道更多的NumPy函数来处理各种数组操作。
numpy阵列:
- 高级数字对象:整数,浮点数
- 容器:列表(无成本的插入和追加),字典(快速查找)
输入:
import numpy as np
a = np.array([0, 1, 2, 3])
print(a)
print(a.ndim)
print(a.shape)输出:
[0 1 2 3] 1 (4,)
输入:
b = np.array([[0, 1, 2], [3, 4, 5]]) # 2 x 3 array print(b.ndim) print(b.shape) len(b)
输出:
2 (2, 3) 2
输入;np.arrange()
a = np.arange(10) # 0 .. n-1 (!) print(a) b = np.arange(1, 9, 2) # start, end (exclusive), step print(b)
输出:
[0 1 2 3 4 5 6 7 8 9] [1 3 5 7]
numpy阵列的创建
arange,linspace,ones,zeros,eye和diag,输入:c = np.linspace(0, 1, 6) # start, end, num-points
print(c)
d = np.linspace(0, 1, 5, endpoint=False)
print(d)
e=np.ones(3)# 或者e=np.ones((3,3)) reminder: (3, 3) is a tuple
print(e)
f=np.eye(3,3)
print(f)
g=np.diag(np.array([1, 2, 3, 4]))
print(g)
h = np.zeros((2, 2))
print(h)
j = np.random.rand(4)
print(j)输出:
[0. 0.2 0.4 0.6 0.8 1. ] [0. 0.2 0.4 0.6 0.8] [1. 1. 1.] [[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]] [[1 0 0 0] [0 2 0 0] [0 0 3 0] [0 0 0 4]] [[0. 0.] [0. 0.]] [0.15299073 0.98066181 0.05337565 0.23230675]
输入:
x=np.arange(1,16).reshape(3,5) x
输出:
array([[ 1, 2, 3, 4, 5], [ 6, 7, 8, 9, 10], [11, 12, 13, 14, 15]])1.3.1.4. Basic visualization
输入:
import matplotlib.pyplot as plt x = np.linspace(0, 3, 20) #start,stop,step y = np.linspace(0, 9, 20) print(x) print(y) plt.plot(x, y) # line plot plt.plot(x, y, 'o') plt.show()
输出:
[0. 0.15789474 0.31578947 0.47368421 0.63157895 0.78947368 0.94736842 1.10526316 1.26315789 1.42105263 1.57894737 1.73684211 1.89473684 2.05263158 2.21052632 2.36842105 2.52631579 2.68421053 2.84210526 3. ] [0. 0.47368421 0.94736842 1.42105263 1.89473684 2.36842105 2.84210526 3.31578947 3.78947368 4.26315789 4.73684211 5.21052632 5.68421053 6.15789474 6.63157895 7.10526316 7.57894737 8.05263158 8.52631579 9. ]
图像显示:
输入:
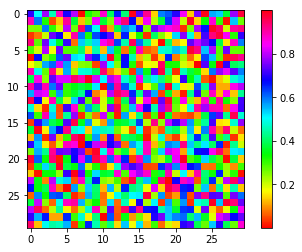
image = np.random.rand(30, 30) plt.imshow(image, cmap=plt.cm.hsv) plt.colorbar() plt.show()
输出:
1.3.1.5. Indexing and slicing
类似于list,标号从零开始
输入:
a = np.arange(10) print(a) print(a[2:9:3]) # [start:end:step]
输出:
[0 1 2 3 4 5 6 7 8 9] [2 5 8]
这张图片可以很好的说明numpy阵列的索引

-
Exercise: Indexing and slicing
-
Try the different flavours of slicing, using
start,endandstep: starting from a linspace, try to obtain odd numbers counting backwards, and even numbers counting forwards. -
Reproduce the slices in the diagram above. You may use the following expression to create the array:
输入:
import numpy as np print(np.arange(6)) print(np.arange(0, 51, 10)[:, np.newaxis]) print(np.arange(6)+np.arange(0, 51, 10)[:, np.newaxis])
输出:
[0 1 2 3 4 5] [[ 0] [10] [20] [30] [40] [50]] [[ 0 1 2 3 4 5] [10 11 12 13 14 15] [20 21 22 23 24 25] [30 31 32 33 34 35] [40 41 42 43 44 45] [50 51 52 53 54 55]]
Exercise: Array creation
Create the following arrays (with correct data types):
Exercise: Array creation Create the following arrays (with correct data types): [[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 2], [1, 6, 1, 1]] [[0., 0., 0., 0., 0.], [2., 0., 0., 0., 0.], [0., 3., 0., 0., 0.], [0., 0., 4., 0., 0.], [0., 0., 0., 5., 0.], [0., 0., 0., 0., 6.]]
输入:
a=np.ones((4,4)) a[2,3]=2 a[3,1]=6 print(a)
输出:
[[1. 1. 1. 1.] [1. 1. 1. 1.] [1. 1. 1. 2.] [1. 6. 1. 1.]]
输入:
b=np.zeros((6,5))
b[1:6,0:5]=np.diag(np.arange(2,7))
b
输出:
array([[0., 0., 0., 0., 0.],
[2., 0., 0., 0., 0.],
[0., 3., 0., 0., 0.],
[0., 0., 4., 0., 0.],
[0., 0., 0., 5., 0.],
[0., 0., 0., 0., 6.]])
1.3.2. Numerical operations on arrays
数组上的数值运算
1.3.2.1. Elementwise operations元素操作
所有的算术运算都是以元素的
输入:
a = np.array([1, 2, 3, 4]) print(a) print(a+1) print(2**a) b = np.ones(4) + 1 print(a*b) #阵列乘法都是以元素为运算单位 print(a.dot(a))#如果想实现矩阵乘法,则采用.dot()运算 a = np.array([1, 1, 0, 0], dtype=bool) b = np.array([1, 0, 1, 0], dtype=bool) print(np.logical_or(a, b)) print(np.logical_and(a, b)) a = np.arange(1,5) print(np.sin(a)) print(np.log(a)) print(np.exp(a)) a = np.triu(np.ones((3, 3)), 1)#构建上三角矩阵 print(a) print(a.T) #矩阵转置
输出:
[1 2 3 4] [2 3 4 5] [ 2 4 8 16] [2. 4. 6. 8.] 30 [ True True True False] [ True False False False] [ 0.84147098 0.90929743 0.14112001 -0.7568025 ] [0. 0.69314718 1.09861229 1.38629436] [ 2.71828183 7.3890561 20.08553692 54.59815003] [[0. 1. 1.] [0. 0. 1.] [0. 0. 0.]] [[0. 0. 0.] [1. 0. 0.] [1. 1. 0.]]
1.3.2.2. Basic reductions
sum(),min(),argmin(),argmax(),mean(),
输入:
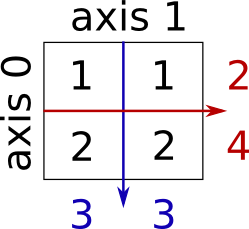
x = np.array([1, 2, 3, 4]) print(x.sum()) x = np.array([[1, 1], [2, 2]]) print(x) print(x.sum(axis=0)) # columns (first dimension) print(x[:, 0].sum(), x[:, 1].sum()) print(x.sum(axis=1)) # rows (second dimension) print(x[0, :].sum(), x[1, :].sum())
输出:
10 [[1 1] [2 2]] [3 3] 3 3 [2 4] 2 4
输入:
x = np.array([1, 2, 3, 4]) print(x.min()) print(x.max()) print(x.argmin()) # index of minimum print(x.argmax()) # index of maximum
输出:
1
4
0
3
输入:
x = np.array([1, 2, 3, 4]) print(x.min()) print(x.max()) print(x.argmin()) # index of minimum print(x.argmax()) # index of maximum print(x.mean()) print(np.median(x)) y = np.array([[1, 2, 3], [5, 6, 1]]) print(y) print(np.median(y, axis=-1)) # last axis print(x.std())
输出:
1 4 0 3 2.5 2.5 [[1 2 3] [5 6 1]] [2. 5.] 1.118033988749895
输入:
a = np.zeros((100, 100)) print(np.any(a != 0)) print(np.all(a == a))
输出:
False
True
工作示例:使用随机游走算法进行扩散

让我们考虑一个简单的一维随机游走过程:在每个步骤中,步行者以相等的概率向右或向左跳。
我们感兴趣的是在t左或右跳之后寻找随机游走者的起源的典型距离?我们将模拟许多“步行者”来找到这条法则,我们将使用数组计算技巧来做到这一点:我们将在一个方向上创建一个带有“故事”(每个步行者都有故事)的2D数组:

左图表示,从原点开始,如果开始第一步选择了向1正方向一定,那么此时位置为1,如果第二部步仍然选择了向正方向1移动,那么此时位置为2
n_stories = 1000 # number of walkers t_max = 200 # time during which we follow the walker t = np.arange(t_max) steps = 2 * np.random.randint(0, 1 + 1, (n_stories, t_max)) - 1 # +1 because the high value is exclusive #随机游走就是一个随机过程,我们让1000个人每次随机游走200步,用上述随机产生1或者-1模拟当前前进过程随机,前进或者 #后退的过程都是随机的 print('steps = ',steps) print('unique(steps) = ',np.unique(steps)) # Verification: all steps are 1 or -1 #We build the walks by summing steps along the time: positions = np.cumsum(steps, axis=1) # axis = 1: dimension of time sq_distance = positions**2 print('positions=',positions) #positions是一个200*1000的结构 print('sq_distance=',sq_distance) #We get the mean in the axis of the stories: mean_sq_distance = np.mean(sq_distance, axis=0) plt.figure(figsize=(4, 3)) plt.plot(t, np.sqrt(mean_sq_distance), 'g.', t, np.sqrt(t), 'y-') plt.xlabel(r"$t$") plt.ylabel(r"$\sqrt{\langle (\delta x)^2 \rangle}$") plt.tight_layout() # provide sufficient space for labels plt.show()
输出:
steps = [[-1 1 -1 ... 1 -1 -1] [ 1 1 -1 ... 1 1 1] [-1 1 -1 ... 1 1 -1] ... [-1 1 1 ... 1 -1 1] [ 1 -1 -1 ... -1 -1 -1] [ 1 1 -1 ... 1 1 -1]] unique(steps) = [-1 1] positions= [[ -1 0 -1 ... 0 -1 -2] [ 1 2 1 ... 2 3 4] [ -1 0 -1 ... 4 5 4] ... [ -1 0 1 ... -20 -21 -20] [ 1 0 -1 ... -10 -11 -12] [ 1 2 1 ... 0 1 0]] sq_distance= [[ 1 0 1 ... 0 1 4] [ 1 4 1 ... 4 9 16] [ 1 0 1 ... 16 25 16] ... [ 1 0 1 ... 400 441 400] [ 1 0 1 ... 100 121 144] [ 1 4 1 ... 0 1 0]]
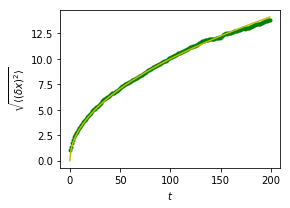
我们发现了一个众所周知的物理结果:RMS距离随着时间的平方根而增长!
1.3.2.3. Broadcasting
以下三种形式得到的最终结果是一样的
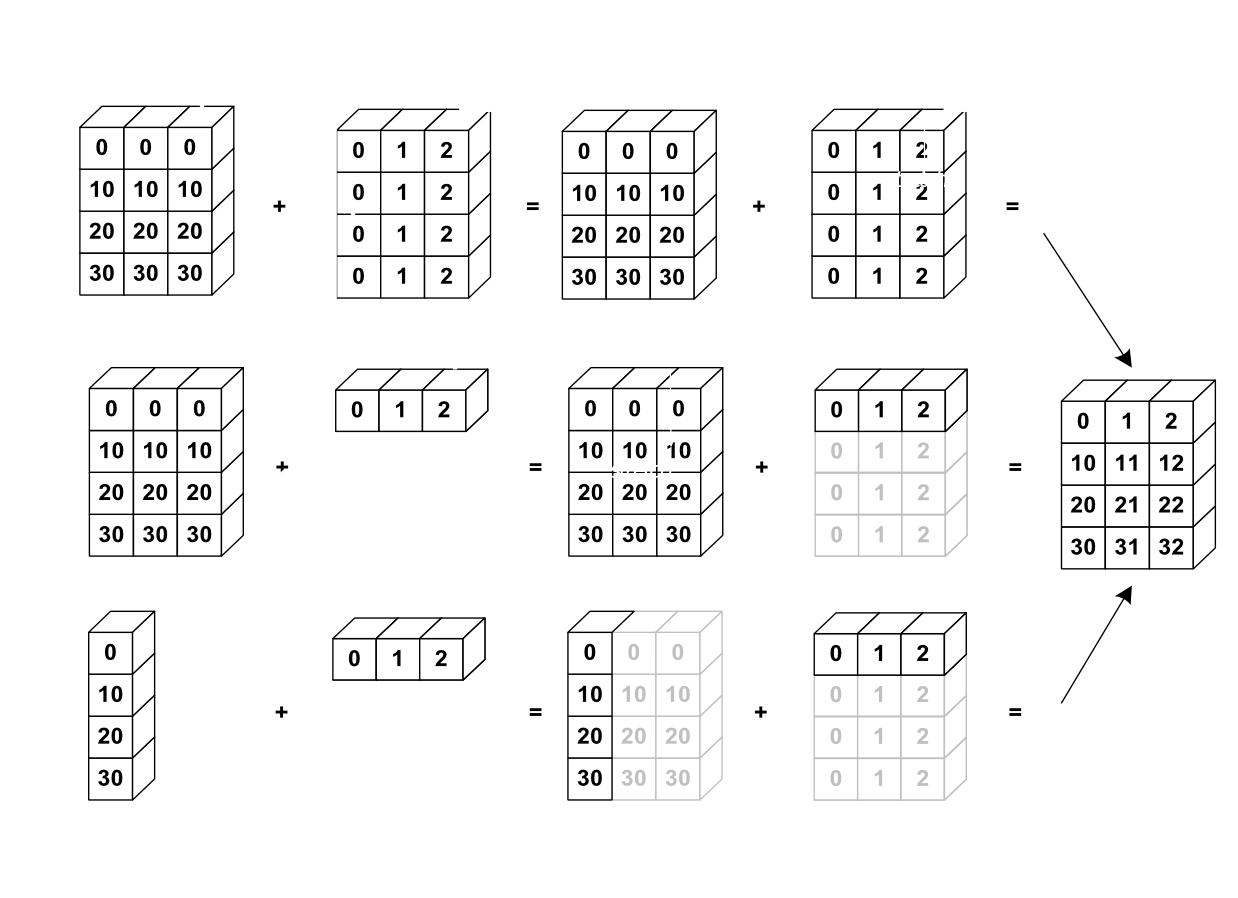
一个实用的trick
输入:
a = np.arange(0, 40, 10) print(a.shape) a = a[:, np.newaxis] # adds a new axis -> 2D array print(a.shape) print('a=',a) print('b=',b) print('a + b=',a+b)
输出:
(4,) (4, 1) a= [[ 0] [10] [20] [30]] b= [ True False True False] a + b= [[ 1 0 1 0] [11 10 11 10] [21 20 21 20] [31 30 31 30]]
输入:
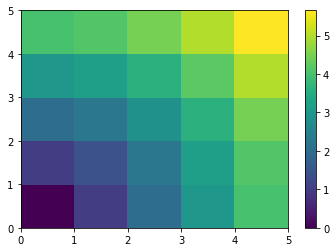
x, y = np.arange(5), np.arange(5)[:, np.newaxis] distance = np.sqrt(x ** 2 + y ** 2) #距离是两者平方之和 print(distance) plt.pcolor(distance) plt.colorbar() plt.show()
输出:
[[0. 1. 2. 3. 4. ] [1. 1.41421356 2.23606798 3.16227766 4.12310563] [2. 2.23606798 2.82842712 3.60555128 4.47213595] [3. 3.16227766 3.60555128 4.24264069 5. ] [4. 4.12310563 4.47213595 5. 5.65685425]]
1.3.2.4. Array shape manipulation
平铺
输入:
a = np.array([[1, 2, 3], [4, 5, 6]]) print(a) print(a.ravel())
输出:
[[1 2 3] [4 5 6]] [1 2 3 4 5 6]
输入:
#注意: reshape may also return a copy!: a = np.zeros((3, 2)) b = a.T.reshape(3*2) b[0] = 9 a
输出:从结果可以看出,a的值并没有发生变化
array([[0., 0.],
[0., 0.],
[0., 0.]])
输入:
z = np.array([1, 2, 3]) print(z) print(z[:, np.newaxis]) print(z[np.newaxis, :])
输出:
[1 2 3] [[1] [2] [3]] [[1 2 3]]
Experiment with transpose for dimension shuffling.
1.3.2.5. Sorting data
输入:
a = np.array([[4, 3, 5], [1, 2, 1]]) b = np.sort(a, axis=1) b
输出:
array([[3, 4, 5],
[1, 1, 2]])
输入:argsort函数,返回值是序列的顺序索引
a = np.array([4, 3, 1, 2]) j = np.argsort(a) print(j) print(a[j])
输出:
[2 3 1 0]
[1 2 3 4]


