树的直径证明+HDU2196

 首先把无向图变成一棵树，直径肯定由叶子组成。

有以下两种情况：        

 

 

 

 

 

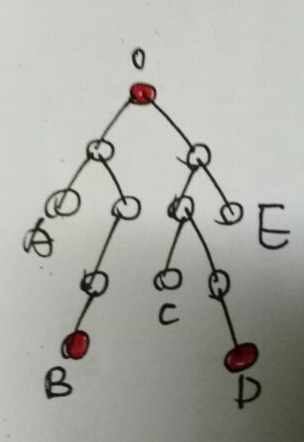
第一种：经过根节点，则找两个最远的叶子肯定是直径，也就是B+D。

 

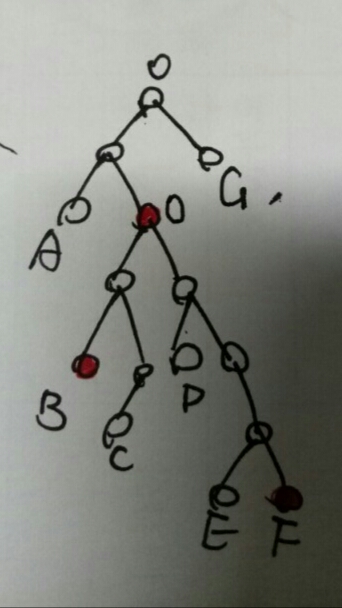
第二种：不经过根节点，则目标的两个叶子肯定有一个不为根的公共祖先，如红点O，则在红点O下面找两个最远的叶子作为直径，找到了C+F。而很明显，这两个目标叶子中的其中一个（F）是距离根最远的叶子，因为如果两个叶子中不包含离根最远的点，则F经过根节点会找到更长的直径，矛盾。

 

则树的直径必然包括一个最远（深）叶子。先搜索到这个点（F），然后再搜索一次最远的点，可以得到树的直径。

这也说明，若把每个点（X）当成一个根，则直径的两个点（C+F）中的一个为X的最远点 ，所以找到直径C+F，则可以找到每个点在无向图中的最远距离：disCX or disFX

 

 

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<vector>
using namespace std;
int dis[10010],ans[10010];
int n,s,t;
vector<int>G[10010];
vector<int>L[10010];
void _dfs(int v)
{
    for(int i=0;i<G[v].size();i++){
        if(!dis[G[v][i]]) {
            dis[G[v][i]]=dis[v]+L[v][i];
            _dfs(G[v][i]);
        }//任意两个点只有一条路，所以dfs和bfs效果一样 
    }
}
void _finds()
{
      memset(dis,0,sizeof(dis));
      dis[1]=1;_dfs(1);s=1;
      for(int i=2;i<=n;i++)
         if(dis[i]>dis[s]) s=i;
     
}
void _findt()
{
      memset(dis,0,sizeof(dis));
      dis[s]=1;_dfs(s);t=1;
      for(int i=2;i<=n;i++)
       if(dis[i]>dis[t]) t=i; 
      for(int i=1;i<=n;i++) ans[i]=dis[i]-1;
}
void _tdis()
{
    memset(dis,0,sizeof(dis));
    dis[t]=1;
    _dfs(t);
    for(int i=1;i<=n;i++)
     if(dis[i]-1>ans[i]) ans[i]=dis[i]-1;
}
int main()
{ 
     int i,j,k,u,v;
     while(~scanf("%d",&n)){
            for(i=1;i<=n;i++) {
               G[i].clear();
               L[i].clear();
            }
            for(i=2;i<=n;i++){
                scanf("%d%d",&u,&v);
                G[u].push_back(i);
                L[u].push_back(v);
                G[i].push_back(u);
                L[i].push_back(v);
            }
            _finds();
            _findt();
            _tdis();
            for(i=1;i<=n;i++)
            printf("%d\n",ans[i]);
     }
     return 0;
}