模糊语意变数、规则和模糊运算--AForge.NET框架的使用（二）

语意变数（Linguistic Variable）

语意变数存储了数个语意量（标签），每个语意量包含一个识别名和模糊集合。在宣告陈述时每个语意量只能和在同一变数中的语意比较。

举个很简单的例子，我们有一个名为temperature的语意变数，它包含4个语意量，名为cold、cool、warm、hot，这也是各自的标签名，同时它们还有各自的隶属度函数。

那么我们就在接下来的系统中使用诸如temperature is hot或者temperature is not hot等等了。

 

//语意变数的声明 
LinguisticVariable lvTemperature = new LinguisticVariable("Temperature", 0, 50);

//模糊集合和隶属度函数 
TrapezoidalFunction function1 = new TrapezoidalFunction(10, 15, TrapezoidalFunction.EdgeType.Right); 
FuzzySet fsCold = new FuzzySet("Cold", function1); 
TrapezoidalFunction function2 = new TrapezoidalFunction(10, 15, 20, 25); 
FuzzySet fsCool = new FuzzySet("Cool", function2); 
TrapezoidalFunction function3 = new TrapezoidalFunction(20, 25, 30, 35); 
FuzzySet fsWarm = new FuzzySet("Warm", function3); 
TrapezoidalFunction function4 = new TrapezoidalFunction(30, 35, TrapezoidalFunction.EdgeType.Left); 
FuzzySet fsHot = new FuzzySet("Hot", function4);

//添加标签 
lvTemperature.AddLabel(fsCold); 
lvTemperature.AddLabel(fsCool); 
lvTemperature.AddLabel(fsWarm); 
lvTemperature.AddLabel(fsHot);

//获取隶属度 
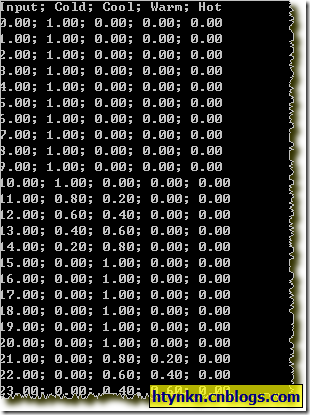
Console.WriteLine("Input; Cold; Cool; Warm; Hot"); 
for (float x = 0; x < 50; x += 1f) 
{ 
    float y1 = lvTemperature.GetLabelMembership("Cold", x); 
    float y2 = lvTemperature.GetLabelMembership("Cool", x); 
    float y3 = lvTemperature.GetLabelMembership("Warm", x); 
    float y4 = lvTemperature.GetLabelMembership("Hot", x);

    Console.WriteLine(String.Format("{0:N}; {1:N}; {2:N}; {3:N}; {4:N}",x, y1, y2, y3, y4)); 
}

 

 

模糊规则（Fuzzy Rule）与数据库（Fuzzy Database）

在拥有语意变数后，我们就创建表述（Statement），它是一种表达，可以做成判断，比如什么是什么，什么不是什么。

而规则（Rule）是可以被模糊系统执行的语意指令。如什么是什么时，就怎么。最简单的就是这种：

IF antecedent THEN consequent

前提（antecedent ）一般由多个由模糊运算符连接的子句组成。如：

...Clause1 AND (Clause2 OR Clause3) AND NOT Clause4 ...

结果（consequent）一般由赋值子句组成，这里的赋值不光是Variable1 IS Value1，Variable1 IS Not Value1同样支持。

举个例子，再创建一个语意变数，Wind，标签有Strong、Breeze、Airless。

那么一下规则就是有效的：

IF Wind IS Strong THEN Temperature IS Cold

IF Wind IS AirlessTHEN Temperature IS NOT Cold

数据库（Fuzzy Database）是一个包含语意变数和相应规则的资料集合，它可以被模糊推理系统（Fuzzy Inference System）使用。

 

//语意变数的声明 
LinguisticVariable lvTemperature = new LinguisticVariable("Temperature", 0, 50);

//模糊集合和隶属度函数 
TrapezoidalFunction function1 = new TrapezoidalFunction(10, 15, TrapezoidalFunction.EdgeType.Right); 
FuzzySet fsCold = new FuzzySet("Cold", function1); 
TrapezoidalFunction function2 = new TrapezoidalFunction(10, 15, 20, 25); 
FuzzySet fsCool = new FuzzySet("Cool", function2); 
TrapezoidalFunction function3 = new TrapezoidalFunction(20, 25, 30, 35); 
FuzzySet fsWarm = new FuzzySet("Warm", function3); 
TrapezoidalFunction function4 = new TrapezoidalFunction(30, 35, TrapezoidalFunction.EdgeType.Left); 
FuzzySet fsHot = new FuzzySet("Hot", function4);

//添加标签 
lvTemperature.AddLabel(fsCold); 
lvTemperature.AddLabel(fsCool); 
lvTemperature.AddLabel(fsWarm); 
lvTemperature.AddLabel(fsHot);

//语意变数的声明 
LinguisticVariable lvWind = new LinguisticVariable("Wind", 0, 50);

//模糊集合和隶属度函数 
TrapezoidalFunction functionw1 = new TrapezoidalFunction(25, 40, TrapezoidalFunction.EdgeType.Right); 
FuzzySet fsStrong = new FuzzySet("Strong", function1); 
TrapezoidalFunction functionw2 = new TrapezoidalFunction(10, 15, 25, 30); 
FuzzySet fsBreeze = new FuzzySet("Breeze", function2); 
TrapezoidalFunction functionw3 = new TrapezoidalFunction(5,10,TrapezoidalFunction.EdgeType.Left); 
FuzzySet fsAirless = new FuzzySet("Airless", function3);

//添加标签 
lvWind.AddLabel(fsStrong); 
lvWind.AddLabel(fsBreeze); 
lvWind.AddLabel(fsAirless);

//创建数据库 
Database db = new Database(); 
db.AddVariable(lvTemperature); 
db.AddVariable(lvWind);

//书写规则 
Rule r1 = new Rule(db, "Thinking1", "IF Wind IS Strong THEN Temperature IS Cold"); 
Rule r2 = new Rule(db, "Thinking2", "IF Wind IS AirlessTHEN Temperature IS NOT Cold"); 

 

模糊运算

以下全是数学相关物…不喜者勿入。

模糊运算主要针对模糊集合，有3种：联集(union)、补集(complement)与交集(intersection)，而依照不同定义有不同的型态。

1.交集中：

标准交集(standard intersection)：t (p,q) = min (p,q)

代数乘积(algebraic product)：t (p,q) = pq

有界差异(bounded different)：t (p,q) = max (0, p+q-1)

彻底交集(drastic intersection)：

2.联集中：

标准联集(standard intersection)：s (p,q) = max (p,q)

代数加法(algebraic product)： s (p,q) = p + q -pq

有界加法(bounded different)： s (p,q) = min (1, p+q)

彻底联集(drastic intersection)：

 

本来还想写模糊合成的…但是没找到可以画矩阵的软件，matlab画出来太丑了。

 

写在最后：

1.本文参考了很多文档和资料，特别是相关英文的对应翻译上，主要参考http://www.academia.edu相关讨论和台湾一些院校的研究报告。

2.有个不错的PPT，可以看一下：http://www.ctdisk.com/file/4479740