模糊集合和隶属度函数--AForge.NET框架的使用(一)
什么是AForge.NET?
AForge.NET是一个为开发人员和研究人员开发的框架,它可以用于计算机视觉,遗传算法,图像处理,神经网络,机器人学习与控制,机器学习和模糊系统。
AForge.NET的官方文档比较丰富,网上也有一些相关文章,但是多是关于视觉和神经网络的,而我个人对模糊系统比较感兴趣,故写下自己的一些感受。
模糊系统和模糊理论简述
模糊系统主要是区别于经典系统(或称为常规系统)。在研究人机系统,管理系统,特别是经济和社会系统时,由于加入人的逻辑、推理、判断,很多决策很难做到完全精确,这些和人有关的系统就拥有了某种模糊性。
在常规系统中,如果一个系统在某刻的状态和输入一旦决定,下个时刻的状态和输出就可以确定。如果下一个状态不能确定,但是可以给出概率分布,就成为随机系统。如果概率分布都不能给出,但是可以给出所有可能状态的集合,而且所有可能状态的集合使用模糊集合来表示,就成为模糊系统。
客观世界中普遍存在着模糊现象,比如“年轻人”和“老年人”就是模糊概念,它们没有明确内涵和外延,但是使用这些概念时却很少产生误解和歧义。可以说值逻辑只是理想世界的模型,而不是现实世界的模型。
隶属度函数(Membership Function)和模糊集合(Fuzzy sets)
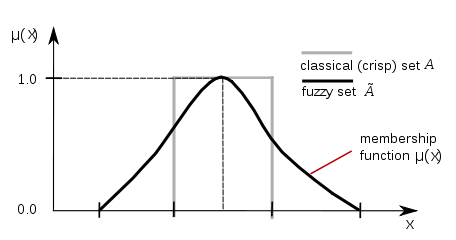
隶属度函数是模糊系统的数学基础,它突破了经典集合理论的局限,模糊概念的定量表示成为可能。
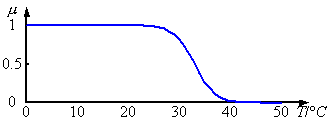
棕色的曲线就是一个隶属度函数,0是不属于,1是完全属于。由于模糊性,所以用[0,1]上的数代替0和1。
而这个值就是就是属于模糊集合的程度。
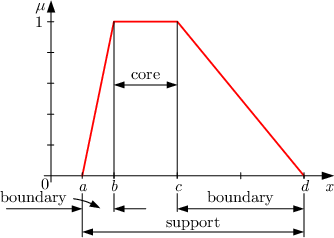
而一个模糊集合可以分为两个部分,其中一个成为core,它是一个每个X的隶属度都是1的宽松集合。
还有一部分成为boundary,它包含了所有隶属度在0,1之间的元素。
隶属度函数的选择主要由模糊集合决定。如果某个集合含有大量的值或者它是连续的,那么一个参数化表示的隶属度函数是适合的,一般分段的线性隶属度函数(Piecewise linear membership functions)是比较好的,它简单而且在计算上是高效的。较常用的是梯形或者三角形,由4或3个参数定义。
以温度为例,在实际生活中我们常说多少度,冷不冷。多少度可以是一个确定的数值或者区间,但是冷不冷就不能固定化,很难找到固定的爆破值。一般可以大致成为冷,暖和,热。
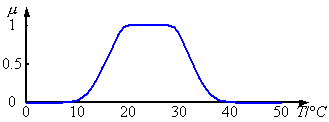
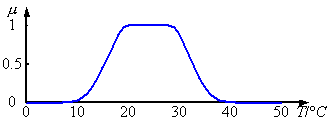
可以认为该隶属度函数为A(x)=暖和。
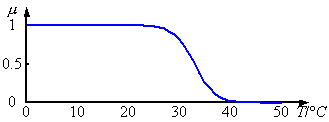
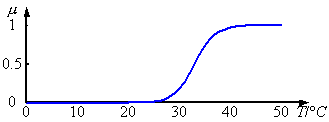
这是热。
AForge.NET表示模糊集合和隶属度函数
需要用到到AForge,AForge.Fuzzy和AForge.Controls。
AForge是核心类,AForge.Fuzzy有关模糊系统的,而AForge.Controls是一些控件,比较常用的是表格(chart)控件。
可以去http://code.google.com/p/aforge/下载,然后引用需要的。我直接用的NuGet。
AForge.Fuzzy在NuGet没有哈。
PiecewiseLinearFunction类无疑是最灵活的,但是如果隶属度函数是梯形或者三角形,有个更快捷的类可供使用:TrapezoidalFunction。
比如我们要建立一个梯形的隶属度函数,如果:
有4个点要注意,(10,0)和(40,0),它们是boundary的边界。(20,0)和(30,0)是core的边界。
TrapezoidalFunction functionCool = new TrapezoidalFunction(10, 20, 30, 40);
FuzzySet fsCool = new FuzzySet("COLD", functionCool);
通过FuzzySet.GetMembership(i)获取隶属度。然后给chart控件一个二维数组就可以绘制了。
double[,] coolValues = new double[50, 2];
for (int i = 0; i < 50; i++)
{
coolValues[i, 0] = i;
coolValues[i, 1] = fsCool.GetMembership(i);
}
chart.UpdateDataSeries("COLD", coolValues);
效果:
当然缺失一半边界的函数也是常用的
关键点是(30,0)和(40,0)。
TrapezoidalFunction functionCool = new TrapezoidalFunction(30,40,TrapezoidalFunction.EdgeType.Right);
FuzzySet fsCool = new FuzzySet("WARM", functionCool);
double[,] coolValues = new double[50, 2];
for (int i = 0; i < 50; i++)
{
coolValues[i, 0] = i;
coolValues[i, 1] = fsCool.GetMembership(i);
}
chart.UpdateDataSeries("WARM", coolValues);
效果:
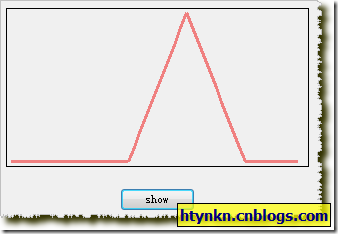
三角形的函数:
TrapezoidalFunction functionCool = new TrapezoidalFunction(20,30,40);
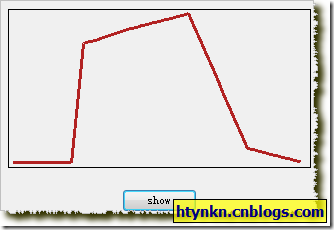
当然PiecewiseLinearFunction可以有更丰富的表现,只需制定其中的关键点就可以构成很多函数了。
AForge.Point[] points = new AForge.Point[6];
points[0] = new AForge.Point(10, 0);
points[1] = new AForge.Point(12, 0.8f);
points[2] = new AForge.Point(20, 0.9f);
points[3] = new AForge.Point(30, 1);
points[4] = new AForge.Point(40, 0.1f);
points[5] = new AForge.Point(50, 0);
PiecewiseLinearFunction membershipFunction = new PiecewiseLinearFunction(points);
FuzzySet fsCool = new FuzzySet("HOT", membershipFunction);
double[,] coolValues = new double[50, 2];
for (int i = 0; i < 50; i++)
{
coolValues[i, 0] = i;
coolValues[i, 1] = fsCool.GetMembership(i);
}
chart.UpdateDataSeries("HOT", coolValues);
效果图:
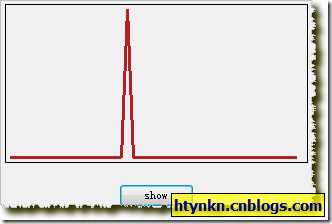
还有一个特别的隶属度函数:SingletonFunction。它只要用于经典数值。
SingletonFunction membershipFunction = new SingletonFunction(20);
作者:黄云坤
出处:http://www.huangyunkun.com/
本文版权归作者所有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。
支持:
新浪微博






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步