图
1.学习总结
1.1图的思维导图
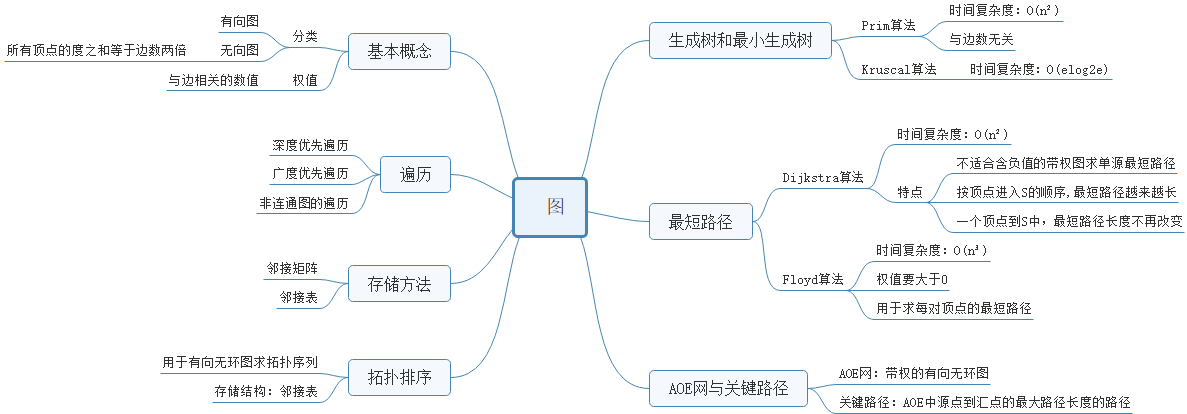
1.2 图结构学习体会
图是一种非线性结构,它的存储方式没有线性存储那么简单易懂易操作。
我们对每一种新知识的 理解都是由浅入深的,从最开始了解无向图有向图的概念,及顶点的出入度概念,还有如何将图的信息存储起来(邻接表和邻接矩阵。
这两种方法各有千秋,对于不同的问题用不同的存储方法,我感觉邻接矩阵的存储方法更为简单直观。
图的遍历有深度和广度两种,深度是从某个点出发,遍历它的任意一个相邻点,以该相邻点为初始顶点,再接着遍历。广度则是先遍历初始顶点的所有相邻点,
再以第一个被访问的相邻点为初始顶点,依此类推。
图的最小生成树可以用Prim和Kruscal算法,Prim是在所挑选的点中寻找最小边,而Kruscal算法是按权值大小连接点,都不能出现回路。
图的最小路径问题可以用Dikstra算法。
拓扑排序是只能运用于有向图寻找拓扑序列的一种排序方法,而且该有向图必须没有环路。
2.PTA实验作业
题目1:1.题目名称7-2:排座位
2. 设计思路


3. 代码截图



4 .PTA提交列表说明。
刚开始编译错误是符号问题,部分正确是因为有一个judge函数在传值时传错,a,b是最开始输入的各种顶点,d,e是后来输入的要检测的顶点,
传值时将a,b传入了judge 函数,导致出错,修改之后正确了。还有,一开始我是将邻接矩阵的值,即edge[][]也一并传入judge函数,可是一直
出错,然后我就把它变成全局变量,就不用再将它进行传值了。
题目2:1.题目名称:7-5:畅通工程之最低成本建设问题
2. 设计思路

3 .代码截图

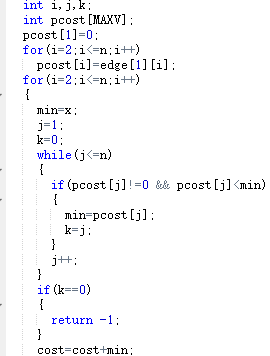
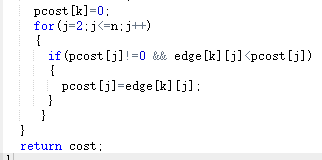
4 .PTA提交列表说明。

一开始多种错误,是因为在输入那边多加了一个变量。
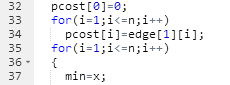
部分错误是因为,在子函数那边给pcost[]赋值时,没有仔细想,应该从i=2开始,而我从i=1开始
改正以后就正确了

题目3:1.题目名称:7-1:图着色问题
2. 设计思路

3 .代码截图
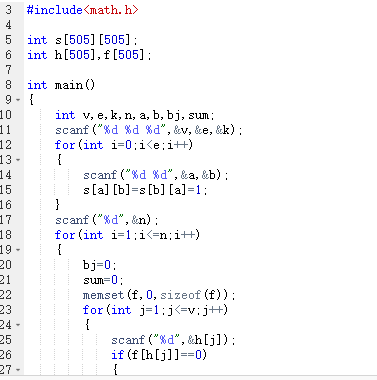

4 .PTA提交列表说明。
这题我一开始想用dfs或者bfs遍历,但是在遍历中,我发现我没办法精准地比较题目给出的颜色种类和给出的数据中的颜色
种类,陷入了一个思维怪圈,而且在遍历算法中也是错误很多。
这题后来问了同学以后借鉴了她的代码,她的代码没有用到图结构,而且思想很简短易懂。
3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的总分:200
4. 阅读代码
这是一篇深度优先遍历的代码,书上进行深度优先遍历时有定义一个全局变量visited[],用于访问标记数组
可是这个代码的作者用了另一种方法,
他的改进是,用函数 ArrayGraph_DFS来创建局部访问标记数组,而真正完成遍历的是ArrayGraph_DFS_traverse,
将visited作为ArrayGraph_DFS_traverse的参数传递,这样递归的各层
函数就能共享这个数组了。
在我看来,这个代码虽然篇幅增长了不少,但是代码的适应性也很大。
#include<stdio.h>
#define MAX_VERTEX 4
typedef char DataType; //图中元素的目标数据类型
typedef struct
{
DataType vertexArr[MAX_VERTEX]; //顶点元素数组
int edgeArr[MAX_VERTEX][MAX_VERTEX]; //边矩阵二维数组
}ArrayGraph;
void ArrayGraph_init(ArrayGraph *pGraph);
void ArrayGraph_create(ArrayGraph *pGraph);
void ArrayGraph_DFS(ArrayGraph * pGraph,int n);
static void ArrayGraph_DFS_traverse(ArrayGraph * pGraph,int n,bool*visited);
int main()
{
ArrayGraph g;
ArrayGraph_init(&g); //初始化图
ArrayGraph_create(&g); //创建图
ArrayGraph_DFS(&g,3); //遍历 ,从索引为3的顶点开始
return 0;
}
//初始化为一个无圈图 ,也就是边矩阵中,主对角线元素都是0
void ArrayGraph_init(ArrayGraph *pGraph)
{
for (int i = 0; i < MAX_VERTEX; i++)
pGraph->edgeArr[i][i] = 0;
}
void ArrayGraph_create(ArrayGraph *pGraph)
{
for (int i = 0; i < MAX_VERTEX; ++i) //填充顶点数组,也就是输入顶点元素
{
printf("输入第%d个顶点值\n",i+1);
scanf(" %c",&(pGraph->vertexArr[i]));
}
for (int j = 0; j <MAX_VERTEX; ++j) //填充边关系
{
for (int i = j+1; i < MAX_VERTEX; ++i)
{
printf("若元素%c和%c有边,则输入1,否则输入0\t",pGraph->vertexArr[j],pGraph->vertexArr[i]);
scanf("%d",&( pGraph->edgeArr[j][i]));
pGraph->edgeArr[i][j] = pGraph->edgeArr[j][i]; //对称
}
}
}
static void ArrayGraph_DFS_traverse(ArrayGraph * pGraph,int n,bool*visited)
{
printf("%c\t",pGraph->vertexArr[n]);
visited[n] = true;
for(int i=0;i<MAX_VERTEX;++i) //以当前已访问的顶点为中心, 在其他所有的顶点中寻找
{
if(pGraph->edgeArr[n][i]!=0 && visited[i]==false) //如果和当前顶点有边,且他们没有被访问过。则访问他们。
{
ArrayGraph_DFS_traverse(pGraph,i,visited);
}
}
for(int i=0;i<MAX_VERTEX;++i) //对图中可能出现的“孤岛”做一次清查
if(visited[i]==false) //如果有孤岛存在,则用同样的方法,遍历他们。
{
ArrayGraph_DFS_traverse(pGraph,i,visited);
}
}
void ArrayGraph_DFS(ArrayGraph * pGraph,int n)
{
bool visited[MAX_VERTEX]; //访问标记数组,
for(int i=0;i<MAX_VERTEX;++i) //局部变量初始化
visited[i] = false;
ArrayGraph_DFS_traverse(pGraph,n,visited);
}

