牛顿迭代法

1. 迭代公式建立

将在点的Taylor展开如下：

一阶泰勒多项式：

近似于

解出x记为，则

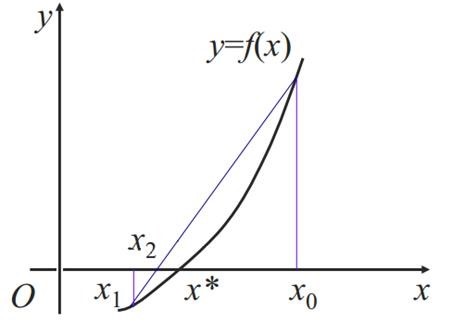
2. 牛顿迭代法的几何解析

在处做曲线的切线，切线方程为：

令得切线与x轴的交点坐标为，这就是牛顿迭代法的迭代公式。因此，牛顿法又称“切线法”。

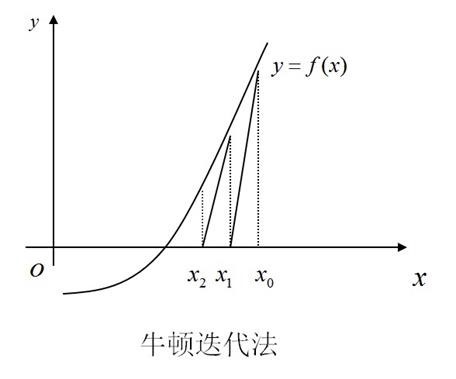
Newton迭代法的特点是：

1. 对初值的选取要求较高。一般的，Newton迭代法只有局部收敛性，当初值在收敛区间里时，收敛速度很快(平方收敛)。但初值离方程根x*较远时，不能保证Newton迭代法收敛。

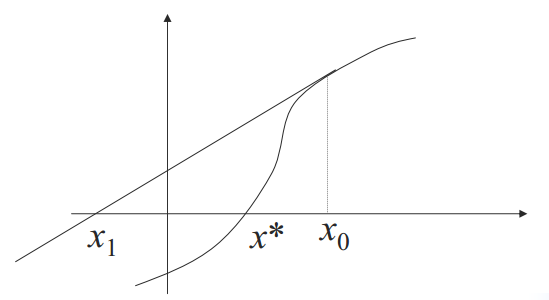
2. Newton迭代法求单根时，收敛速度很快(平方收敛)。但如果方程根是重根，则收敛速度较慢，且重数越高速度越慢。但当是m重根时,用下面的迭代格式：

则至少能保持平方收敛。

3.应用：用有Newton迭代法求

求解：设，则

取

程序实现：

#define ABS(VAL) (((VAL)>0)?(VAL):(-(VAL)))   
//用牛顿迭代法求浮点数的平方根   
double mysqrt(float x) {   
    double g0,g1;   
    if(x==0) 
        return 0;   
    g0=x/2;   //初值
    g1=(g0+x/g0)/2;   
    while(ABS(g1-g0)>0.01) //终止条件  
    {   
        g0=g1;   
        g1=(g0+(x/g0))/2;   //迭代规则
    }   
    return g1;   
}

或

double sqr(double n) {
    double k=1.0;
    while(abs(k*k-n)>1e-9) {
        k=(k+n/k)/2;
    }
    return k;
}

附加：

1. Newton下山法

由于当初值离方程根较远时，不能保证Newton迭代法收敛，但一旦进入收敛区间，则收敛速度很快。为使尽快进入收敛区间，常采用Newton下山法：

称为下山因子

具体做法如下：

1. 选取初值
2. 取下山因子（可修改）
3. 计算
4. 计算并比较与的大小：
若，则
         1） 当时，取，结束；
         2） 当时，将作为新的值继续计算；
若，则取，返回3。

2. 弦截法（方程常用的求解方法）

将Newton切线法中的切线斜率用弦的斜率替换：