问题描述:对树的遍历有,前序遍历,后序遍历。(注意,这里前后序的定义是指节点本身和它的子结点之间的访问顺序关系,而不是某个节点的子结点之间的访问顺序关系,即这里的序指的是父子关系,而非子间关系)。对二叉树又有中序遍历(特别的,对二叉查找树的中序遍历,是一个有序序列)。
由于树的递归性,所以这些遍历采用递归函数实现非常直观简便。但对于一个给定的二叉树,要求手工计算出各种序遍历结果时,由于递归函数从计算机实现角度易于理解,而从手工演算来说并不适合,所以我采用了一种虚拟路径穿过序点的方法来实现手工给出一个二叉树的遍历结果。
该路径从根节点进入,饶树环绕一周,从根节点退出完成。当路径穿过节点的序点时,输出/访问该节点。如下图说是:左侧是范例二叉树(该范例来自《系统设计师(高级程序员)教程》P428页,王春森主编),右侧则给出了虚拟路径。
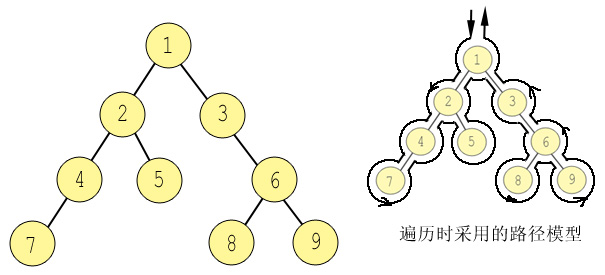
针对上面的范例二叉树,假设有一个行人,用右侧的路径绕着树行进时,并始终尝试向逆时针方向转动,游历节点的顺序如下:
1 -> 2-> 4-> 7 -> 4 -> 2 -> 5 -> 2 -> 1 -> 3 - > 6 - > 8 -> 6 -> 9 -> 6 -> 3 - > 1;
在环绕节点转动时,只要能够知道自己相对于节点所处的方位,就可以根据这个方位信息知道在当前遍历序下,是否应访问该节点。
为了完成上面的方法,首先要知道行人所在位置相对于节点的方位,因此按照如下方式定义树节点的序点,即针对二叉树的某个节点,从12点方向逆时针环绕该节点一周,在这个圆周型路径上将依次经过一共 7 个关键节点,如下图所示:
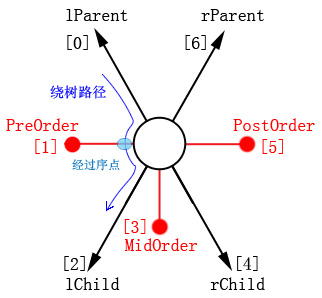
注意,当从某个子节点沿着指针回到其父节点时, 我们需要明确知道自己所处的方位。所以就必须知道子结点指向父节点的连线的方向。因此,上面的定义中,必须还要给出父节点位于自身的哪个方向(左侧还是右侧),即需要定义左父/右父指针,这是和普通的树不同的所在。普通的树的父节点仅仅体现在子结点“上方”,是没有相对于子结点的方向信息的!
这样给出一个二叉树的结构图,我们就可以在草稿纸上很容易的给出三种序遍历的结果。现在我们将采用代码实现上面的方法,根据上图模型,给出节点的定义,它将有一个包含 7 个元素的指针数组来描述路径上面的关键节点,把图中红色的点(索引为 1,3, 5)称之为序点,它们固定为 NULL,即当路径经过这些特殊点时,是访问该节点的时机(每个序点对应特定的遍历序,已标注于图中)。其他元素属于指向其他节点的连线方向(这些节点是指向其他节点的实际指针),例如左右子结点,父节点等。很显然,节点的 lParent 和 rParent 至多只有一个不为 NULL,如果两者都为 NULL,它是二叉树的根节点。
代码实际上就是模拟了沿着虚拟路径进行行进,当经过指向其他节点的指针时,进入其他节点(饶着树的结构主干行进),当经过序点时,访问该节点即可。范例代码如下:
#include <stdio.h> #include <stdlib.h> #include <string.h> #define POINTER_COUNT 7 enum PointerIndexs { IDX_LPARENT = 0, IDX_ORDER_PRE = 1, IDX_LCHILD = 2, IDX_ORDER_MID = 3, IDX_RCHILD = 4, IDX_ORDER_POST = 5, IDX_RPARENT = 6, }; typedef struct tagNODE { int val; struct tagNODE* p[POINTER_COUNT]; } NODE, *PNODE; //访问节点 void Visit(PNODE pNode) { if(pNode != NULL) _tprintf(_T("%ld "), pNode->val); } //当从一个节点进入另一个节点时,位于节点内的方位需要更新 int UpdateIndex(int index) { //先进行180度翻转 int newIndex = (index >= 4) ? (index - 4): (index + 4); //需要立即向前走动一格 return (newIndex + 1)% POINTER_COUNT; } void Travel(PNODE pRoot, int order) { int index = IDX_LPARENT, i; //根节点的序点数 int rootVisitTimes = 0; PNODE pNode = pRoot; while(1) { //从某个位置进入,然后遍历所有指针,并且需回到起始点 for(i = 0; i < POINTER_COUNT; i++) { if(pNode->p[index] != NULL) { //enter next Node pNode = pNode->p[index]; //更新索引 index = UpdateIndex(index); break; } else { if(index == order) Visit(pNode); //如果index 是1,3, 5,表示该索引是输出序点 //如果根节点的三个序点都已经访问完成,则说明对树的遍历已完成 if(pNode == pRoot && (index & 1)) { ++rootVisitTimes; if(rootVisitTimes == 3) return; } } index = (index + 1) % POINTER_COUNT; } } } //对某个节点插入子结点 PNODE InsertChild(PNODE pParent, int iChild, int val) { //插入前该子结点位置必须为NULL!否则覆盖它会导致内存泄露! if(pParent != NULL && pParent->p[iChild] != NULL) return NULL; PNODE pChild = (PNODE)malloc(sizeof(NODE)); memset(pChild, 0, sizeof(NODE)); if(pParent != NULL) pParent->p[iChild] = pChild; pChild->val = val; if(iChild == IDX_LCHILD) pChild->p[IDX_RPARENT] = pParent; else pChild->p[IDX_LPARENT] = pParent; return pChild; } //创建一个二叉树的实例demo PNODE BuildDemoTree() { PNODE pNode1 = InsertChild(NULL, IDX_LCHILD, 1); PNODE pNode2 = InsertChild(pNode1, IDX_LCHILD, 2); PNODE pNode3 = InsertChild(pNode1, IDX_RCHILD, 3); PNODE pNode4 = InsertChild(pNode2, IDX_LCHILD, 4); PNODE pNode5 = InsertChild(pNode2, IDX_RCHILD, 5); PNODE pNode6 = InsertChild(pNode3, IDX_RCHILD, 6); PNODE pNode7 = InsertChild(pNode4, IDX_LCHILD, 7); PNODE pNode8 = InsertChild(pNode6, IDX_LCHILD, 8); PNODE pNode9 = InsertChild(pNode6, IDX_RCHILD, 9); return pNode1; } //释放二叉树占用的内存 void FreeTree(PNODE pRoot) { if(pRoot != NULL) { FreeTree(pRoot->p[IDX_LCHILD]); FreeTree(pRoot->p[IDX_RCHILD]); free(pRoot); } } int _tmain(int argc, _TCHAR* argv[]) { int i; TCHAR* names[] = { _T("Pre "), _T("Mid "), _T("Post") }; int orders[] = { IDX_ORDER_PRE, IDX_ORDER_MID, IDX_ORDER_POST }; PNODE pRoot = BuildDemoTree(); for(i = 0; i < 3; i++) { _tprintf(_T("Travel %s Order: "), names[i]); Travel(pRoot, orders[i]); printf("\n"); } //释放二叉树占用的内存 FreeTree(pRoot); pRoot = NULL; getchar(); return 0; }
范例代码中,构建了图 1 中的范例二叉树,并分别用前序,中序,后序进行了遍历。Visit为访问节点函数,目前它仅仅是把节点的值进行打印输出。该程序产生的输出如下:
Travel Pre Order: 1 2 4 7 5 3 6 8 9 Travel Mid Order: 7 4 2 5 1 3 8 6 9 Travel Post Order: 7 4 5 2 8 9 6 3 1
总结:
优点是,组建树时,额外描述了节点的父节点以及该父节点相对于它的方向性,这样我们就可以实现一个相对简单的形式单一的遍历函数(Travel),完成二叉树的所有三种方式遍历,仅需要在参数中指定序点即可。该遍历函数不是递归函数(因此不像递归函数那样会在栈上堆叠较多的 stack frame),代码简单易读,对树的遍历就好像在遍历一个线性链表一样。
缺点是,而该方法每个节点将包含 7 个指针(比普通的二叉树描述占用内存要高),并且一半以上是 NULL 指针,如果树节点太多,内存方面将需要权衡和优化。对于树这种结构,由于完整树的内存需求关于树深度的增长速度太快,所以如果树规模较大,都要慎重考虑内存需求的限制。换句话说,应当仅尝试在内存中建立较小规模的树。
参考资料:
王春森,系统设计师(高级程序员)教程,清华大学出版社。
【补充后记】
多年前,小玉学妹(littlehead)曾向我请教用栈去改写树的遍历问题,在当时因为我没有学习过相关知识,所以给出的自己的想法可能是不切实际的(但我已记不清当初给的是什么想法,大概是在树节点上增加标识一类的),也没有给出实现。很遗憾当初我的能力和知识的有限实际上我未能给出什么帮助。多年后我偶然半夜里冒出这个点子然后把我的方法用代码实现了。本文所述的方法也是通过在树节点上增加信息量来实现的,从空间使用上来说实际上只是把状态由辅助栈转移到了节点数据上而已,因此它是一种可选方法,但不属于改进方法。以此文献给小玉(littlehead)学妹。



