蜂窝状网格的定位方法

      所谓蜂窝状网格，也就是由多个六边形组成的类似蜂窝的网格，在一些游戏地图编辑器，手机触摸屏，泡泡龙游戏等场景可以看到使用这种蜂窝网格。对于普通的矩形网格来说（例如俄罗斯方块，贪吃蛇的棋盘），由于屏幕和位图在逻辑上的点阵模型，使得矩形网格的定位非常简便。矩形网格如果按照边连接，具有 4 临域（上下左右），而按照顶点连接，具有 8 临域（在前者基础上加上对角线）；蜂窝网格的行间是一种错位关系，这使得我们编程建立数据结构模型时带来一点不便。下面仅从直观观察描述该网格（实际编程实现时还需要根据具体情况而定）。蜂窝网格具有 6 临域，例如在下面的图中，就是左，右，上偏左，上偏右，下偏左，下偏右。当我们把蜂窝网格的数据也用数组存储时，蜂窝网格的临域和存储结构有关。如下图在行间交错的情况下，6 临域是在 8 临域 的基础上去掉了两个元素（去掉的元素根据所在奇数行和偶数行有所不同），在编程时这些是需要注意的地方。

　　蜂窝网格的捕获并不是那么直观的，本文将讲解如何在蜂窝网格定位，换句话说，也就是给定一个屏幕坐标，需要判断哪个网格被该坐标选中。首先我们来看蜂窝网格定位的原理，由下图所示：

      

      在上面的蜂窝网格上，我用蓝色线条绘制了一张矩形网格（暂时称为网格A）。并用蓝色圆点在图上标记了每个蜂窝网格的中心点。我们根据给定的坐标（x，y）可以首先定位到网格A中的某个矩形网格，然后观察“网格A”和“蜂窝网格”的关系可以发现，每个网格A的矩形网格的边缘上都分布了三个蜂窝网格的中心点。这样我们就可以在这三个点中找出与（x，y）点距离最近的点，也就完成了蜂窝网格定位。

      需要注意的是，蜂窝网格由于存在一种错位关系，因此蜂窝网格的中心点落到矩形网格A上时，是行间交替变化的。例如在我所画的这张图上，我在图片右侧绘制除了网格A的纵坐标为奇数和偶数时的蜂窝点分布情况。在捕获蜂窝网格时，必须针对这一点特别处理。

      网格A中的单个矩形网格宽度和高度在代码中分别是 g_unitx 和 g_unity;  它们分别是 网格A 在两个方向上的长度单位。
      假设六边形的边长为 a ，则：

      g_unitx = a * sqrt (3) ;
      g_unity = a * (3/2) ;

      下面我们就给出捕获蜂窝网格的重要代码：
      void GetCell(int x, int y, int *lpCellX, int *lpCellY);
      （x，y）通常为鼠标的当前位置，调用后，通过 lpCellX 和 lpCellY 参数返回被捕获的网格的中心点坐标。

#pragma once
#include "stdafx.h"

//蜂窝网格的定位方法 -- by hoodlum1980
//假设六边形的边长为a；


//两个方向的矩形定位的基本单位
#define unitx(a)    ((a)*1.7320508)  //sqrt(3) * a
#define unity(a)    ((a)*1.5)                    //1.5 * a


//两个方向的矩形网格基本单位
double g_unitx;
double g_unity;
double g_MinDistance2;     // (a*sqrt(3)/2)^2

//设置六边形的边长
void SetCellSize(int a)
{
    if(a>0)
    {
        g_unitx = unitx(a);
        g_unity = unity(a);
        
        //二分之根号3 边长的平方，如果距离比它还小，就必然捕获
        g_MinDistance2 = a*a*0.75;
    }
}


//求取两个点的距离平方
inline int distance2(int x1, int y1, int x2, int y2)
{
    return ((x2-x1)*(x2-x1) + (y2-y1)*(y2-y1));
}


//输入鼠标按下的点坐标（x，y）
//返回被捕获六边形的中心坐标
void GetCell(int x, int y, int *lpCellX, int *lpCellY)
{
    //位于矩形网格边线上的三个CELL中心点
    POINT points[3];
    //当前距离
    int dist;
    int mindist= (int)(g_MinDistance2 * 100); //一个非常大的值
    int i, index;//index:被捕获的索引
    //计算出鼠标点位于哪一个矩形网格中
    int cx = (int)(x/g_unitx);
    int cy = (int)(y/g_unity);
    
    points[0].x = (int)(g_unitx * cx);
    points[1].x = (int)(g_unitx * (cx+0.5));
    points[2].x = (int)(g_unitx * (cx+1));
    //根据cy是否是偶数，决定三个点的纵坐标
    if(cy % 2 == 0)
    {
        //偶数时，三个点组成倒立三角
        points[0].y = points[2].y = (int)(g_unity * cy);
        points[1].y = (int)(g_unity * (cy+1));
    }    
    else
    {
        //奇数时，三个点组成正立三角
        points[0].y = points[2].y = (int)(g_unity * (cy+1));
        points[1].y = (int)(g_unity * cy);
    }
    
    //现在找出鼠标距离哪一个点最近
    for(i=0;i<3;i++)
    {
        //求出距离的平方
        dist = distance2(x,y, points[i].x, points[i].y);
        
        //如果已经肯定被捕获
        if(dist < g_MinDistance2)
        {
            index = i;
            break;
        }
        
        //更新最小距离值和索引
        if(dist < mindist)
        {
            mindist = dist;
            index = i;
        }
    }    
    
    //现在index 就是被捕获的结果
    *lpCellX = points[index].x;
    *lpCellY = points[index].y;    
}

//给出蜂窝CELL的中心点和边长a，填充Cell的六边形的六个端点

void GetCellPoints(int cellx, int celly, int a, POINT *lpPoints)
{
    if(lpPoints == NULL) return;
        
    lpPoints[0].x = cellx;
    lpPoints[0].y = celly - a;
    
    lpPoints[1].x = cellx + (int)(g_unitx*0.5);
    lpPoints[1].y = celly - a/2; 
    
    lpPoints[2].x = lpPoints[1].x;
    lpPoints[2].y = celly + a/2;
    
    lpPoints[3].x = cellx;
    lpPoints[3].y = celly + a;
    
    lpPoints[4].x = cellx - (int)(g_unitx*0.5);
    lpPoints[4].y = celly + a/2;
    
    lpPoints[5].x = lpPoints[4].x;
    lpPoints[5].y = celly - a/2;
}

　　除了上面我实现的距离法以外，我们还可以根据角度法，求出被捕获的CELL；原理如下图所示：

　　

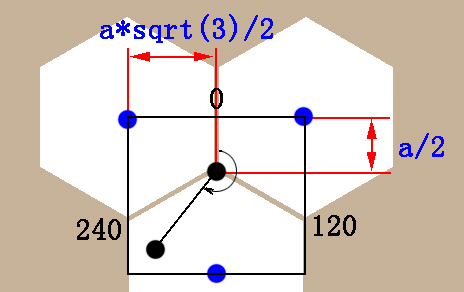
　　如上图所示，很显然，同样要区分 y 是偶数还是奇数。这里我们就其中一种情况讨论，在上图中，我们可以很容易获取到三个 CELL 的交界点的坐标：
　　ox = g_unitx * x + a * sqrt(3)/2;
　　oy = g_unity * y + a/2;

　　然后我们求出鼠标点和交界点的偏离12点的角度值：（需要考虑y轴和笛卡尔坐标的方向相反，还要考虑点所在的象限，这里我们简单起见，不去讨论）

　　alpha = 90 - atan( (oy - y) / (x - ox))  ;
　　if （alpha < 0)  alpha += 180 ;

　　然后根据该角度落在的区间，得出被捕获的 CELL 的中心点坐标；
　　这种实现方法需要考虑的情况要比距离法更复杂，不易读一些，因此这里我就不去尝试写出完成的代码了。

      下面我给出一个 Windows 应用程序作为上面的代码的演示，该程序首先绘制一副蜂窝网格图背景，然后当鼠标在窗口上移动时，窗口实时的反馈被鼠标捕获的网格（用蓝色显示），程序运行效果如图：

      

      该范例的源代码下载链接：
      https://files.cnblogs.com/hoodlum1980/BeehiveCell.rar