数据挖掘实践-第一个简单案例-地图着色数据自动分级
通过公司培训机会了解到SPSS Modeler这个工具,可以方便地实现数据挖掘算法。故今后将数据挖掘领域的学习与实践做一记录。
案例目标###
- 假设要将一个数据集投射在地图上,希望分成5级色阶:红、橙、黄、绿、蓝。红色表示数值高、蓝色表示数值低。那么怎样划分色阶等级最合理?
- 目前常见的简单做法有:1. 等数量分级;2. 等数值分级。以1000个记录为例,前者按照排序后每200个记录为一级,后者是按最大值和最小值的差值等分5级。在某些数据分布时,两种方法都有不妥之处:前者容易导致分级边界不合理(相近的数据被分到两级),后者容易导致分级大小不均衡(个别等级只有极少数数据)。
- 那么是否存在一种规则,可以评价分级方法的合理性。并建立一种基于数据集实现自动分级的方法?
案例实践###
- 第一个问题比较玄奥,无论是抽象的规则(基于数学语言)还是具象的解释(基于主观感知),暂时很难建立一个判别标准。
- 一个比较容易想到的描述是“假设一种划分方案,使得5个分级总的均方误差最小”,这个看似相当合理,但是目前无法证明其是否最合理。
- 而按照上述“描述”,容易想到这很类似K-means聚类方法,而且是只有单个输入变量的简单聚类。
- 获得聚类结果后,找出各聚类的上下极值,就可以确定分级边界了。
-
选用一个移动小区的流量统计数据。这类数据一般都符合长尾分布。

-
使用Modeler中的默认设置,得到K-means聚类结果
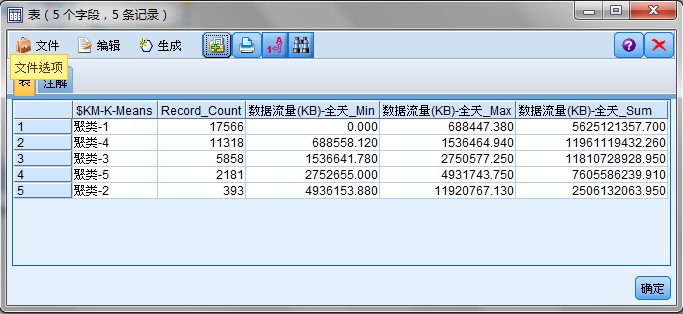
-
等数量划分、等数值划分、聚类划分三种结果的比较。其中自己杜撰了几个指标
所以聚类得到的类的大小是不太均匀的,但是肯定好于等数值划分。
-
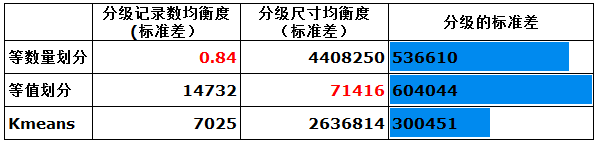
试着对比一下等数量划分,等数值划分,de和聚类划分的均方差。
-
结论:聚类划分的分级记录数均衡度优于等值划分,分级尺寸均衡度优于等数量划分,整体的标准差最佳
后续思考###
- 聚类得到的分级边界一般不是整数,不符合习惯。优化方法是可以增加限制条件,迭代时以某整数段作归属判断。
- 在考虑代码实现时又想到,未必要对原始数据集进行kmeans聚类运算。可以先按设想的整数段分组,再对组进行聚类。当然计算距离的公式要重定义,要经组大小来加权。
首次发布:2014.07.22





