『TensotFlow』转置卷积
网上解释
作者:张萌
链接:https://www.zhihu.com/question/43609045/answer/120266511
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
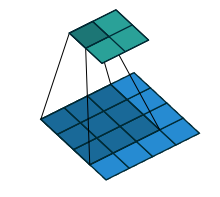
不难想象 其实就是如下的稀疏阵:
其实就是如下的稀疏阵:
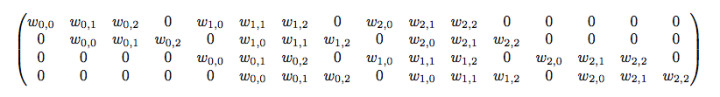
链接:https://www.zhihu.com/question/43609045/answer/120266511
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
一句话解释:逆卷积相对于卷积在神经网络结构的正向和反向传播中做相反的运算。
逆卷积(Deconvolution)比较容易引起误会,转置卷积(Transposed Convolution)是一个更为合适的叫法.
举个栗子:
4x4的输入,卷积Kernel为3x3, 没有Padding / Stride, 则输出为2x2。
输入矩阵可展开为16维向量,记作
输出矩阵可展开为4维向量,记作
卷积运算可表示为
不难想象
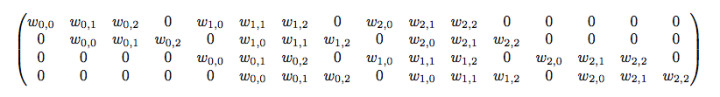
平时神经网络中的正向传播就是转换成了如上矩阵运算。
那么当反向传播时又会如何呢?首先我们已经有从更深层的网络中得到的.
回想第一句话,你猜的没错,所谓逆卷积其实就是正向时左乘,而反向时左乘
,即
的运算。
补充理解
下图标注有误,“SAME”应为“VALID”,kernel为3,stride为1,卷积输出为(输入-核+1)/步长。

tensorflow接口
tf.nn.conv2d_transpose()
kernel = tf.random_normal(shape=[2,2,3,1])
# strides 和padding也是假想中 正向卷积的模样。当然,x是正向卷积后的模样
y = tf.nn.conv2d_transpose(x,kernel,output_shape=[1,5,5,3],
strides=[1,2,2,1],padding="SAME")
# 在这里,output_shape=[1,6,6,3]也可以,考虑正向过程,[1,6,6,3]
# 通过kernel_shape:[2,2,3,1],strides:[1,2,2,1]也可以
注意:conv2d_transpose 中会计算 output_shape 能否通过给定的参数计算出 inputs的维度,如果不能,则报错。





