【CF 675D Tree Construction】BST

题目链接：http://codeforces.com/problemset/problem/675/D

题意：给一个由n个互异整数组成的序列a[]，模拟BST的插入过程，依次输出每插入一个元素a[i]后a[i]的父节点。

数据范围：n [2, 10^5]

思路：直接模拟一般的BST而不维护平衡性的话，有可能会出现极度不平衡甚至退化的情况，复杂度会从O(nlogn)上升到O(n^2)。因此要用平衡二叉树。

可以利用STL中的set容器，但对于题目所要找的“父节点”，set并不提供接口。这时就要考察BST的一些性质推导出解法。

回顾二叉树的中序遍历，对节点prev的直接后继succ的定位操作分两种情况。注意等价BST的“上下可变，左右不乱”的性质，不论是否进行了等价变换，中序遍历序列中任意两个互为直接前驱和直接后继的元素，其层次关系必然为如下两种之一：

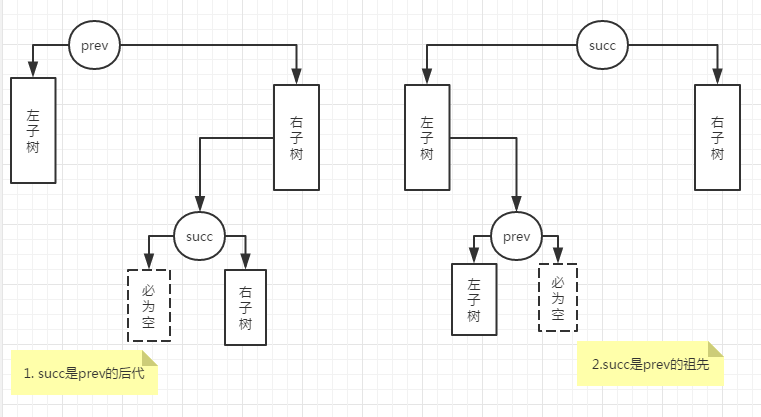
1. succ层次更深

=> 由顺序性，succ必为prev的右子树中的节点，故prev的右子树必非空；

　　且由“直接性”，succ的左孩子必为空。

　　对于v小于全局最小值的边界情况，prev及其左子树为空。

2. prev层次更深

=> 由顺序性，prev必为succ的左子树中的节点，故succ的左子树必非空；

　　且由“直接性”，prev的右孩子必为空。

　　对于v大于全局最大值的边界情况，succ及其右子树为空。

 

对于一个新的待插入的节点v，我们在当前BST的中序遍历序列 s 中进行二分查找，得到应插入的位置的后继元素的位置succ（“大于v的第一个元素，即upper_bound”），然后得到prev=succ-1。为了保证BST的顺序性，v必然要插在prev和succ之间。

从树的结构上看，可以插在标有“必为空”的位置，它恰好介于prev和succ之间，顺序性必然得到保证。具体地，即“succ和prev中更深的那个”，1、2两种情况分别对应succ和prev。如何确定是哪种情况呢？

 

我们回到对这两种情况的描述上：刚刚所做的推导是否可逆呢？如果可逆，那么我们可以通过判断succ或prev的左右孩子是否为空就可以得知是哪种情况。

分析发现，确实可逆：

1. succ的左孩子为空 => 由顺序性，prev必为succ的祖先 => succ层次更深。

2. prev的右孩子为空 => 由顺序性，succ必为prev的祖先 => prev层次更深。

 

到此，可以着手设计算法了。首先用set维护平衡二叉树，每次插入节点v前，调用set的lower_bound(或upper_bound，元素互异故二者无差别) 得到“大于v的第一个元素”，即插入v后v的直接后继，记录为迭代器succ。然后得到succ的直接前驱的迭代器prev = succ - 1。

对于左右孩子情况的记录，我没有想到方法，CF题解给出的是维护两个map<int, int>left, right，left记录节点对<v, lc>，right记录节点对<v, rc>。每次插入前通过判断left[succ]和right[prev]是否为空来判断父节点是谁，以及v作为左孩子还是右孩子插入，更新map。

其实这两种情况是对立的，因此一次判断就可确定属于哪种。

#include <cstdio>
#include <cstring>
#include <set>
#include <map>
using namespace std;
const int MAX_N = 100005;

int n;
struct Node
{
    int d;
    int lc, rc;
    Node(){}
    Node(int d):d(d), lc(-1), rc(-1){}
}nodes[MAX_N];

int a[MAX_N];

int main()
{
    while(~scanf("%d", &n)){
        for(int i=0; i<n; i++){
            scanf("%d", &a[i]);
        }
        set<int> s;
        map<int, int> left;//<节点，左孩子> 
        map<int, int> right; //<节点,右孩子> 
        int res;
        s.insert(a[0]);
        for(int i=1; i<n; i++){
            set<int>::iterator pos = s.lower_bound(a[i]);//直接后继 
            if(pos != s.end() && left.count(*pos)==0){//后继没有左孩子，插到后继的左孩子位置
                res = *pos;
                left[*pos] = a[i];
            }else{//后继有左孩子，或没有后继，插到前驱的右孩子位置 
                pos--;
                res = *pos;
                right[*pos] = a[i];
            }
            printf("%d ", res);
            s.insert(a[i]);
        }
        printf("\n");
    }
    return 0;
}

p.s: CF题解的代码好优美，学习了。