训练神经网络,其中一个加速训练的方法就是归一化输入。
假设我们有一个训练集,它有两个输入特征,即输入特征x是二维的,
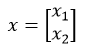
下图是数据集的散点图。
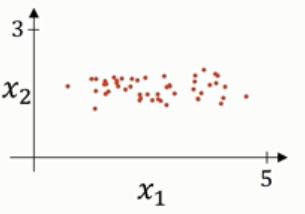
归一化输入需要两个步骤,第一步是零均值化,即每个元素减去均值操作,公式如下:

结果如下图:

第二步是,归一化方差,上图中,特征x1的方差比特征x2的方差要大的多,处理如下:

最后,数据分布形式如下图:
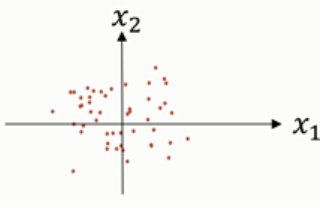
此时,x1和x2的方差都等于1。
如果你在训练数据进行归一化后,那么就要用与训练数据相同的μ和σ来归一化测试集。
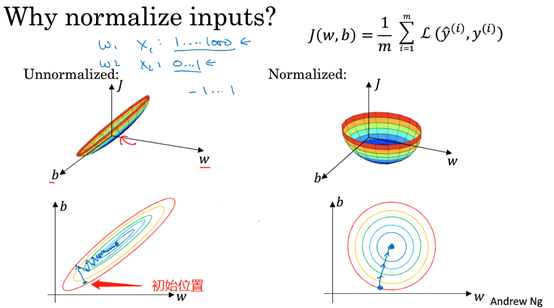
为什么我们要将输入特征归一化?
回想一下,代价函数的定义为:
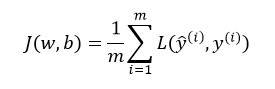
如果你使用非归一化的输入特征,那么代价函数将会像下图左侧图那样,这是一个非常细长狭窄的代价函数。如果x1的取值范围从1到1000,x2的范围是从0到1,结果是参数w1和w2的范围或比率将会非常不同。如果你能画出该函数的部分轮廓,它会是这样一个狭长的函数。然而,如果你归一化特征,代价函数平均起来更对称。如果你在左图这样的代价函数上运行梯度下降法,你必须使用一个非常小的学习率,因为如果初始位置位于下图红色箭头的位置,梯度下降法可能需要多次迭代过程,直到找到最小值。但如果函数是一个更圆的球形轮廓,那么不论从哪个位置开始,梯度下降法都能够更直接地找到最小值,你可以在梯度下降法中使用较大步长,而不需要像在左图那样反复执行。当然,实际上w是一个高维向量,因此用二维绘制w并不能正确地传达直观理解,但总的直观理解是当特征都在相似范围内时,代价函数会更圆一点,而且更容易优化。
实际上,如果假设特征x1范围在0~1之间,x2范围在-1~1之间,x3范围在1~2之间,它们的范围比较相似,所以会表现得很好;当它们范围相差很大时,如x1范围在0~1000之间,那么这对优化算法非常不利。
所以,如果输入特征处于不同的范围,而且范围相差比较大,那么归一化特征值就非常重要了。如果特征值处于相似范围,那么归一化就不是很重要,但执行归一化也没有坏处。因此当不确定归一化是否可以提高训练或者算法速度时,可以使用归一化操作。


