为什么正则化有利于预防过拟合,为什么它可以减少方差问题?
下面通过两个例子来直观体会。
下面的图中,左图是高偏差,右图是高方差,中间的是just right

现在我们来看看一个庞大的深度拟合神经网络,下面的网络不够大,深度也不够,但你可以想象这是一个过拟合的神经网络,
我们的代价函数J含有参数w和b,公式如下:
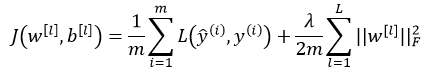
从损失函数中可以看出,从直观上理解,如果正则化参数λ设置足够大,权重矩阵W会被设置为接近于0的值。直观理解就是把多隐藏单元的权重设为接近0,于是基本消除了这些隐藏单元的许多影响,如下图,被打“X”的神经元将消失,这种情况下,原来的神经网络将会被大大的简化,即变成一个很小的网络,但深度却很深,那么这个状态将会使得网络从高方差的状态趋向于高偏差的状态。但是λ存在一个中间状态,使得网络会接近一个“just right”的中间状态。
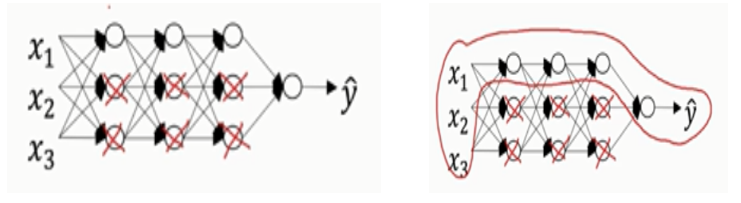
直观理解就是λ增加到足够大,W会接近于0,实际上是不会发生这种情况的,我们尝试消除或者至少减少许多隐藏单元的影响,最终这个网络会变得更加简单,这个神经网络会越来越接近逻辑回归。
我们直觉上认为大量隐藏单元被完全消除了,其实不然,实际上是该神经网络的所有隐藏单元依然存在,但是它们的影响变得更小了,神经网络变得更简单了,貌似只有更不容易发生过拟合。
-------------------------------------------------------------------------------------------
另外一种解释
假设我们使用的是双曲(tanh)激活函数,g(z)=tanh(z),该激活函数的特点是,当z的绝对值很小时,曲线可以近似看成线性状态,当z的绝对值变得更大时,激活函数开始变得非线性。
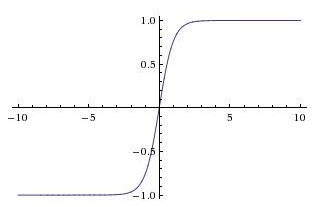
因此,如果正则化参数λ很大时,权重W将会变得很小,由于z=Wx+b,因此会造成z也会变得很小(忽略b的影响),如果z的值在上面说的线性范围之内,那么g(z)大致呈线性,那么神经网络每一层几乎都是线性的,和线性回归一样,那么整个网络就是一个线性网络,即使是一个很深的网络,因为具有线性激活函数的特征,最终我们只能计算线性函数,因此它不适合用于非常复杂的决策,从而没法过度拟合数据集的非线性决策边界。


