Latent Dirichlet Allocation(LDA)

变量：

$w$表示词，$z$表示主题，$\mathbf{w}=(w_1,w_2,\cdots,w_N)$表示文档，语料库$D = (\mathbf{w}_1,\cdots,\mathbf{w}_M)$，$V$表示所有单词的个数（固定值），$N$表示一个文档中的词数（随机变量），$M$是语料库中的文档数（固定值），$k$是主题的个数（预先给定，固定值）。

 

在说明LDA模型之前，先介绍几个简单一些的模型。

1.Unigram model:

文档$\mathbf{w}=(w_1,w_2,\cdots,w_N)$，用$p({{w}_{n}})$表示词${{w}_{n}}$的先验概率，生成文档$\mathbf{w}$的概率：$p(\mathbf{w})=\prod\limits_{n=1}^{N}{p({{w}_{n}})}$。

图模型为：

 

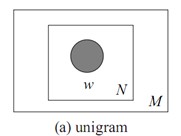
2.Mixture of unigrams model:

一篇文档只由一个主题生成。该模型的生成过程是：给某个文档先选择一个主题$z$，再根据该主题生成文档，该文档中的所有词都来自一个主题。假设主题有${{z}_{1}},...,{{z}_{k}},$生成文档$\mathbf{w}$的概率为：

$p(\mathbf{w})=p({{z}_{1}})\prod\limits_{n=1}^{N}{p({{w}_{n}}|{{z}_{1}})}+\cdots +p({{z}_{k}})\prod\limits_{n=1}^{N}{p({{w}_{n}}|{{z}_{k}})}=\sum\limits_{z}{p(z)\prod\limits_{n=1}^{N}{p({{w}_{n}}|z)}}.$

图模型为：

 

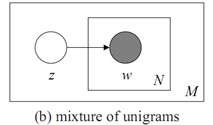
LDA模型：

下面说明LDA模型生成一个文档的过程：

1首先要选择一个主题概率分布$\theta$，$\theta =({{\theta }_{1}},...,{{\theta }_{k}}),{{\theta }_{i}}$代表第i个主题被选择的概率，即$p(z=i|\theta )={{\theta }_{i}}$，且$\sum\limits_{i=1}^{k}{{{\theta }_{i}}}=1$，$\theta \thicksim Dir(\alpha )$，$p(\theta |\alpha )=\frac{\Gamma (\sum\limits_{i=1}^{k}{{{\alpha }_{i}}})}{\prod\limits_{i=1}^{k}{\Gamma ({{\alpha }_{i}})}}\theta _{1}^{{{\alpha }_{1}}-1}\cdots \theta _{k}^{{{\alpha }_{k}}-1}.$

2在选好一个主题概率分布$\theta $后，再选择一个主题${{z}_{n}}$，再根据${{z}_{n}}$和$\beta $选择一个词${{w}_{n}}$。$\beta ={{({{\beta }_{ij}})}_{k\times V}},{{\beta }_{ij}}=p({{w}^{j}}=1|{{z}^{i}}=1)$表示主题$i$生成词$j$的概率，$\sum_{j=1}^V \beta_{ij}=1$。

用2中的步骤生成N个词，文档$\mathbf{w}$就生成了。

图模型：

 

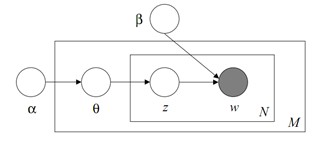
由LDA的图模型我们可以清楚得看出变量间的依赖关系。

整个图的联合概率（单个文档）为：$p(\theta, \mathbf{z},,\mathbf{w}|\alpha,\beta)=p(\theta|\alpha)\prod_{n=1}^Np(z_n|\theta)p(w_n|z_n,\beta)$，

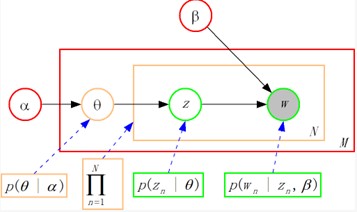
生成文档的概率为$p(\mathbf{w}|\alpha,\beta)=\int p(\theta|\alpha)\prod_{n=1}^N\sum_{z_n}p(z_n|\theta)p(w_n|z_n,\beta)d\theta$，文本语料库由$M$篇文档组成，$D = (\mathbf{w}_1,\cdots,\mathbf{w}_M)$，故生成文本语料库的概率为

$p(D|\alpha,\beta)=\prod_{d=1}^M \int p(\theta_d|\alpha)\prod_{n=1}^{N_d} $$\sum_{z_{d_n}}p(z_{d_n}|\theta_d) p(w_{d_n}|z_{d_n},\beta)d\theta_d.$

下面叙述训练过程：

首先设定目标函数

\[\ell(\alpha,\beta)=\log p(D|\alpha,\beta)=\log \prod_{d=1}^M p(\mathbf{w}_d|\alpha,\beta)=\sum_{d=1}^M\log p(\mathbf{w}_d|\alpha,\beta).\]

我们参数训练的目标是求使$\ell(\alpha,\beta)$最大的参数$\alpha^\ast,\beta^\ast$。我们把$p(\mathbf{w}|\alpha,\beta)$展开得$p(\mathbf{w}|\alpha,\beta)=\frac{\Gamma(\sum_i \alpha_i)}{\prod_i \Gamma(\alpha_i)}\int(\prod_{i=1}^k \theta_i^{\alpha_i-1})(\prod_{n=1}^N\sum_{i=1}^k\prod_{j=1}^V(\theta_i\beta_{ij})^{w_n^j})d\theta$，由于$\theta$和$\beta$的耦合，对$\ell(\alpha,\beta)$用极大似然估计难以计算。下面我们用变分EM算法来计算最优参数$\alpha,\beta$。

E步骤：我们用$L(\gamma,\phi;\alpha,\beta)$来近似估计$\log p(\mathbf{w}|\alpha,\beta)$，给定一对参数值$(\alpha,\beta)$，针对每一文档，求得变分参数$\{\gamma_d^\ast,\phi_d^\ast:d\in D\}$，使得$L(\gamma,\phi;\alpha,\beta)$达到最大。

M步骤：求使$\mathscr{L}=\sum_d L(\gamma_d^\ast,\phi_d^\ast;\alpha,\beta)$达到最大的$\alpha,\beta$。

重复E、M步骤直到收敛，得到最优参数$\alpha^\ast,\beta^\ast$。

E步骤的计算方法：

这里用的是变分推理方法(variational inference)，文档的似然函数

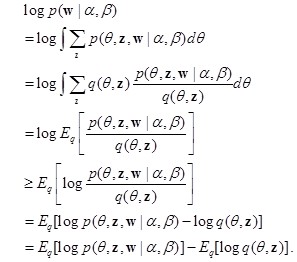
上式右部记为$L(\gamma,\phi;\alpha,\beta)$。当$\frac{ p(\theta,\mathbf{z},\mathbf{w}|\alpha,\beta)}{ q(\theta,\mathbf{z})}$为常数时，上式取等号，即分布$q$取$p(\theta,\mathbf{z}|\mathbf{w},\alpha,\beta)$时。

$p(\theta,\mathbf{z}|\mathbf{w},\alpha,\beta)=\frac{ p(\theta,\mathbf{z},\mathbf{w}|\alpha,\beta)}{ p(\mathbf{w}|\alpha,\beta)}$，由于$p(\mathbf{w}|\alpha,\beta)$中$\theta$和$\beta$的耦合，$p(\mathbf{w}|\alpha,\beta)$难以计算，因此$p(\theta,\mathbf{z}|\mathbf{w},\alpha,\beta)$也难以计算。我们用分布$q(\theta,\mathbf{z}|\gamma,\phi)$来近似分布$p(\theta,\mathbf{z}|\mathbf{w},\alpha,\beta)$，在$L(\gamma,\phi;\alpha,\beta)$中分布$q$取$q(\theta,\mathbf{z}|\gamma,\phi)$，我们得$\log p(\mathbf{w}|\alpha,\beta)= L(\gamma,\phi;\alpha,\beta)+D(q(\theta,\mathbf{z}|\gamma,\phi)|| p(\theta,\mathbf{z}|\mathbf{w},\alpha,\beta)).$上式说明计算分布$q(\theta,\mathbf{z}|\gamma,\phi)$与分布$p(\theta,\mathbf{z}|\mathbf{w},\alpha,\beta))$间的KL距离的最小值等价于计算下界函数$L(\gamma,\phi;\alpha,\beta)$的最大值。

用来近似后验概率分布$p(\theta,\mathbf{z}|\mathbf{w},\alpha,\beta))$的分布$q(\theta,\mathbf{z}|\gamma,\phi)$的图模型：

 

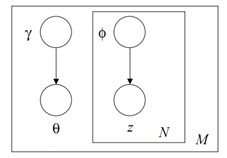
$\gamma$为狄利克莱分布的参数，$\phi=(\phi_{ni})_{n \times i},n=1,\cdots,N,i=1,\cdots,k$，$\phi_{ni}$表示第$n$个词由主题$i$生成的概率，$\sum_{i=1}^k \phi_{ni}=1$。

下面我们求使$L(\gamma,\phi;\alpha,\beta)$达到极大的参数$\gamma^\ast,\phi^\ast$。

将$L(\gamma,\phi;\alpha,\beta)$中的$p$和$q$分解，得

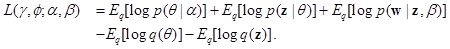
把参数$(\alpha,\beta)$和$(\gamma,\phi)$代入$L(\gamma,\phi;\alpha,\beta)$，再利用公式$E_q[\log(\theta_i)|\gamma]=\Psi(\gamma_i)-\Psi(\sum_{j=1}^k \gamma_j)$（$\Psi$是$\log\Gamma$的一阶导数，可通过泰勒近似来计算），我们可得到

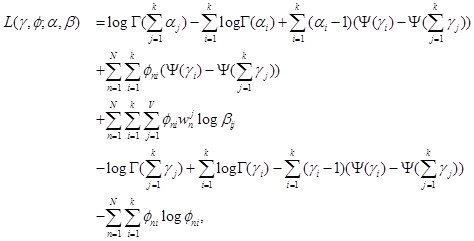
然后用拉格朗日乘子法（即变量的拉格朗日函数对变量求偏导等于零，求出变量对应的等式）来计算可得

$\phi_{ni} \propto \beta_{iv} \text{exp}(\Psi(\gamma_i)-\Psi(\sum_{j=1}^k \gamma_j)),$

$\gamma_i=\alpha_i+\sum_{n=1}^N \phi_{ni}.$

由$\sum_{i=1}^k \phi_{ni}=1$归一化求得$\phi_{ni}$。由于解$\phi_{ni}$和$\gamma_i$相互影响，可用迭代法来求解，算法如下：

 

最终可以得到收敛的参数$\gamma^\ast,\phi^\ast$。这里的参数$\gamma^\ast,\phi^\ast$是在给定一个固定的文档$\mathbf{w}$下产生的，因此$\gamma^\ast,\phi^\ast$也可记为$\gamma^\ast(\mathbf{w}),\phi^\ast(\mathbf{w})$，变分分布$q(\theta,\mathbf{z}|\gamma^\ast(\mathbf{w}),\phi^\ast(\mathbf{w}))$是后验分布$p(\theta,\mathbf{z}|\mathbf{w},\alpha,\beta)$的近似。文本语料库$D = (\mathbf{w}_1,\cdots,\mathbf{w}_M)$，用上述方法求得变分参数$\{\gamma^\ast_d,\phi^\ast_d:d \in D\}$。

M步骤的计算方法：

将$\{\gamma^\ast_d,\phi^\ast_d:d \in D\}$代入$\sum_d L(\gamma_d,\phi_d;\alpha,\beta)$得$\mathscr{L}=\sum_d L(\gamma_d^\ast,\phi_d^\ast;\alpha,\beta)$，我们用拉格朗日乘子法求$\beta$，拉格朗日函数为$l=\mathscr{L}+\sum_{i=1}^k \lambda_i(\sum_{j=1}^V \beta_{ij}-1)$，求得$\beta_{ij} \propto \sum_{d=1}^M \sum_{n=1}^{N_d} \phi_{dni} w_{dn}^j$，由$\sum_{j=1}^V \beta_{ij}=1$归一化求得$\beta_{ij}$。

下面求$\alpha$。我们对拉格朗日函数$l$对$\alpha_i$求偏导，得$\frac{\partial l}{\partial {\alpha_i}}=M(\Psi(\sum_{j=1}^k \alpha_j)-\Psi(\alpha_i))+\sum_{d=1}^M(\Psi(\gamma_{di})-\Psi(\sum_{j=1}^k \gamma_{dj}))$。由这个偏导等式可知$\alpha_i$值和$\alpha_j$值($i \neq j$)之间相互影响，故我们得用迭代法来求解最优$\alpha$值。我们用牛顿-拉弗逊算法来求解。将上面的偏导数再对$\alpha_j$求偏导，得$\frac{\partial l}{\partial {\alpha_i} \partial{\alpha_j}}=M(\Psi^{\prime}(\sum_{j=1}^k \alpha_j)-\delta(i,j) \Psi^{\prime}(\alpha_i))$。牛顿-拉弗逊算法的迭代公式为$\alpha_{\text{new}}=\alpha_{\text{old}}-H(\alpha_{\text{old}})^{-1}g(\alpha_{\text{old}})$，$H(\alpha)$即$\frac{\partial l}{\partial {\alpha_i} \partial{\alpha_j}}$，$g(\alpha)$即$\frac{\partial l}{\partial {\alpha}}$，迭代到收敛时即得最优$\alpha$值。

测试新文档主题分布：

设新文档为$\mathbf{w}$，用变分推理算法计算出新文档的$\gamma^\ast,\phi^\ast$，由于$\phi_{ni}$表示文档中第$n$个词由主题$i$生成的概率，故$\sum_{n=1}^N \phi_{ni}$为对文档中由主题$i$生成的词数估计，$\frac{1}{N}\sum_{n=1}^N \phi_{ni}$为主题$i$在文档主题组成中的比重。

上述说法与推导有错的话请大家批评指正。