使用最大似然法来求解线性模型（1）

在Coursera机器学习课程中，第一篇练习就是如何使用最小均方差(Least Square)来求解线性模型中的参数。本文从概率论的角度---最大化似然函数，来求解模型参数，得到线性模型。本文内容来源于：《A First Course of Machine Learning》中的第一章和第二章。

 

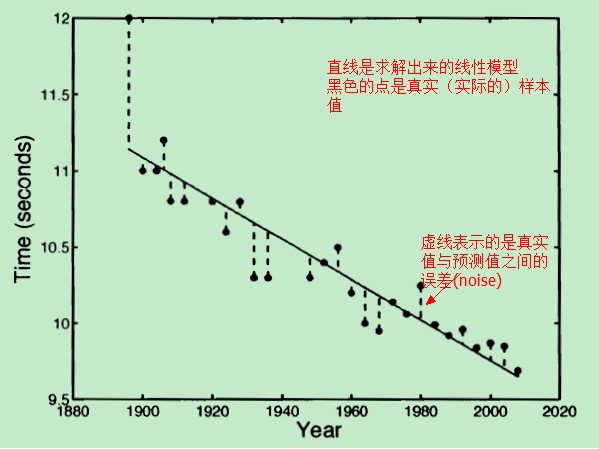
先来看一个线性模型的例子，奥林匹克百米赛跑的男子组历年数据如下：

 

 

所谓求得一个线性模型就是：给定一组数据(上图中的很多点)，如何找到一条合适的直线，让这条直线能够更好地“匹配”这些点。

一种方式就是使用最小二乘法，通过最小化下面的代价函数J(θ)求得一条直线方程--即线性模型。

 

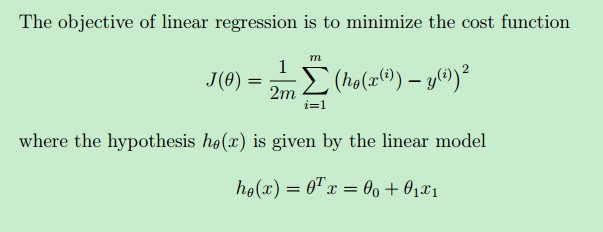
其中，h_θ(x)是待求解的线性模型(本例中就是一条直线)，y⁽ⁱ⁾是样本x⁽ⁱ⁾对应的实际值，h_θ(x⁽ⁱ⁾)是线性模型在样本x⁽ⁱ⁾上的预测值。我们的目标就是让实际值与预测值二者尽可能地接近--二者之间的“差”尽可能地小，这样我们的预测结果就越准确，我们的线性模型也越好(不考虑overfitting)

最小二乘法就是最小化J(θ)这个函数，解出θ，代入h_θ(x)，得到一条直线(h_θ(x)就是直线方程)。而这条直线，就是我们的线性模型了。

 

对于这种方式而言，我们的模型就是一条直线，在我们的模型中（直线）没有能够反映真实值与预测值之间的误差的因子。把模型稍微修改一下：

从原来的：(这里的w就相当于上面的θ，t 就是h_θ(x)，只是为了统一 一下《A First Course of Machine Learning》中用到的符号)

t=w^T*x

改成：

t=w^T*x+ξ

其中，ξ 用来表示“误差”---noise，x是训练样本数据，w是模型的参数。

 

这样，我们的新模型表达式：t=w^T*x+ξ 就可以显示地表示 noise 了(不仅仅是一条直线表达式了)。那现在问题还是：怎样求得一个“最好的” w 和 ξ，得到“最好的”模型？

 

现在不是用上面的最小二乘法了求解w 和 ξ 了，而是用最大似然函数法---（见使用最大似然法来求解线性模型（2）-为什么是最大化似然函数？）

 

原文：http://www.cnblogs.com/hapjin/p/6623127.html