MLlib--GBDT算法

转载请标明出处http://www.cnblogs.com/haozhengfei/p/8b9cb1875288d9f6cfc2f5a9b2f10eac.html 

---

GBDT算法

江湖传言：GBDT算法堪称算法界的倚天剑屠龙刀

 

GBDT算法主要由三个部分组成：

 

                   – 

Regression Decistion Tree（即

DT)

   

回归树

                   – 

Gradient Boosting（即GB)

   

迭代提升

                   – 

Shrinkage(渐变)

   

渐变

1.决策树

1.1决策树的分类

决策树	分类决策树	用于分类标签值，如晴天/阴天/雾/雨、用户性别、网页是否是垃圾页面。
	回归决策树	预测实数值，如明天的温度、用户的年龄、网页的相关程度

强调：回归决策树的结果（数值）加减是有意义的，但是分类决策树是没有意义的，因为它是类别

1.2什么是回归决策树？

   回归树决策树的总体流程可以类比分类树，比如C4.5分类树在每次分枝时，是穷举每一个feature的每一

个阈值，找到使得按照feature<=阈值，和feature>阈值分成的两个分枝的熵最大的feature和阈值，按照该标准分枝得到两个新节点，用同样方法继续分枝直到所有人都被分入性别唯一的叶子节点，或达到预设的终止条

件，若最终叶子节点中的性别不唯一，则以多数人的性别作为该叶子节点的性别。在回归树当中，每个节点（不一定是叶子节点）都会得一个预测值，以年龄为例，该预测值等于属于这个节点的所有人年龄的平

均值。分枝时穷举每一个feature的每个阈值找最好的分割点，但衡量最好的标准不再是最大熵，而是最小化均方差--即（每个人的年龄-预测年龄）^2 的总和 / N，或者说是每个人的预测误差平方和 除以 N。这很好理解

，被预测出错的人数越多，错的越离谱，均方差就越大，通过最小化均方差能够找到最靠谱的分枝依据。分枝直到每个叶子节点上人的年龄都唯一（这太难了）或者达到预设的终止条件（如叶子个数上限），若最终叶子

节点上人的年龄不唯一，则以该节点上所有人的平均年龄做为该叶子节点的预测年龄。

1.3回归决策树划分的原则_CART算法

   CART算法思想：计算子节点的均方差，均方差越小，回归决策树越好。

2.GBDT算法_Boosting迭代

   即通过迭代多棵树来共同决策

   GBDT的核心就在于，每一棵树学的是之前所有树结论和的残差(比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵

树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学)，这个残差就是一个加预测值后能得真实值的累加量。这一过程离不开Boosting迭代。

2.2图解Boosting迭代

 

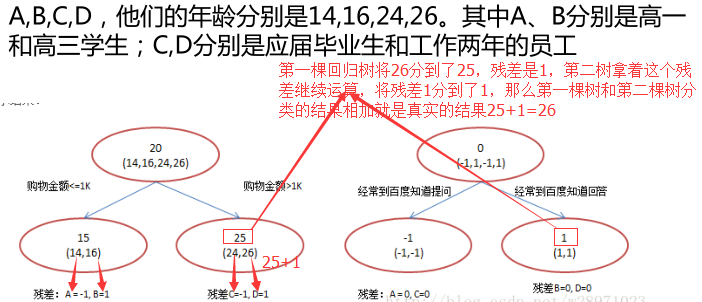
Adaboost算法是另一种boost方法，它按分类对错，分配不同的weight，计算时使用这些weight，从而让“错分的样本权重越来越大，使它们更被重视”。

 

2.3GBDT算法_构建决策树的步骤

• 0. 表示给定一个初始值

• 1. 表示建立M棵决策树（迭代M次）

• 2. 表示对函数估计值F(x)进行Logistic变换

• 3. 表示对于K个分类进行下面的操作（其实这个for循环也可以理解为向量的操作，每一个样本点xi都对应了K种可能的分类yi，所以yi, F(xi), p(xi)都是一个K维的向量，这样或许容易理解一点）

• 4. 表示求得残差减少的梯度方向

• 5. 表示根据每一个样本点x，与其残差减少的梯度方向，得到一棵由J个叶子节点组成的决策树

• 6. 为当决策树建立完成后，通过这个公式，可以得到每一个叶子节点的增益（这个增益在预测的时候用的）

每个增益的组成其实也是一个K维的向量，表示如果在决策树预测的过程中，如果某一个样本点掉入了这个叶子节点，则其对应的K个分类的值是多少。比如说，GBDT得到了三棵决策树，一个样本点在预测的时候，也会掉入3个叶子节点上，其增益分别为（假设为3分类的问题）： (0.5, 0.8, 0.1), (0.2, 0.6, 0.3), (0.4, 0.3, 0.3)，那么这样最终得到的分类为第二个，因为选择分类2的决策树是最多的。

• 7. 将当前得到的决策树与之前的那些决策树合并起来，作为新的一个模型

2.4GBDT和其他的比较

2.4.1GBDT和随机森林的比较

问题：GBDT和随机森林都是基于决策树的高级算法，都可以用来做分类和回归，那么什么时候用GBDT？ 什么时候用随机森林？

    1.二者构建树的差异：

            随机森林采取有放回的抽样构建的每棵树基本是一样的，多棵树形成森林，采用投票机制决定最终的结果。

            GBDT通常只有第一个树是完整的，当预测值和真实值有一定差距时（残差），下一棵树的构建会拿到上一棵树最终的残差作为当前树的输入。GBDT每次关注的不是预测错误的样本，没有对错一说，只有离标准相差的远近。

    2.因为二者构建树的差异，随机森林采用有放回的抽样进行构建决策树，所以随机森林相对于GBDT来说对于异常数据不是很敏感，但是GBDT不断的关注残差，导致最后的结果会非常的准确，不会出现欠拟合的情况，但是异常数据会干扰最后的决策。

    综上所述：如果数据中异常值较多，那么采用随机森林，否则采用GBDT。

2.4.2GBDT和SVM

GBDT和SVM是最接近于神经网络的算法，神经网络每增加一层计算量呈几何级增加，神经网络在计算的时候倒着推，每得到一个结果，增加一些成分的权重，神经网络内部就是通过不同的层次来训练，然后增加比较重要的特征，降低那些没有用对结果影响很小的维度的权重，这些过程在运行的时候都是内部自动做。如果GBDT内部核函数是线性回归（逻辑回归），并且这些回归的离散化，归一化做得非常好，那么就可以赶得上神经网络。GBDT底层是线性组合来给我们做分类或者拟合，如果层次太深，或者迭代次数太多，就可能出现过拟合，比如原来用一条线分开的两种数据，我们使用多条线来分类。

2.4.3如何用回归决策树来进行分类？

   把回归决策树最终的叶子节点上面的数据进行一个逻辑变换（logistic），然后对这样的数据进行逻辑回归，就可以使用回归决策树来进行分类了。

2.4.4数据处理--归一化

归一化：

   不同的特征数量级不一样，（第一个特征0-1，第二个特征1000-10000，这时候就需要归一化，都归一到0-1之间）

 

归一化两种方式：

   线性归一化 (x-min)/(max-min)

   零均值归一化 （与期望和方差有关）；

2.5回归决策树code

生成测试数据LogisticRegressionDataGenerator

回归决策树代码测试GBDT_new

   bootstingStrategy.setLearningRate(0.8)`//设置梯度，迭代的快慢

import org.apache.log4j.{Level, Logger}
import org.apache.spark.mllib.feature.{StandardScaler, StandardScalerModel}
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.tree.{GradientBoostedTrees, DecisionTree}
import org.apache.spark.mllib.tree.configuration.{BoostingStrategy, Algo}
import org.apache.spark.mllib.tree.impurity.Entropy
import org.apache.spark.mllib.util.MLUtils
import org.apache.spark.rdd.RDD
import org.apache.spark.{SparkConf, SparkContext}

/**
  * Created by hzf
  */
object GBDT_new {
//    E:\IDEA_Projects\mlib\data\GBDT\train E:\IDEA_Projects\mlib\data\GBDT\train\model 10 local
    def main(args: Array[String]) {
        Logger.getLogger("org.apache.spark").setLevel(Level.ERROR)
        if (args.length < 4) {
            System.err.println("Usage: DecisionTrees <inputPath> <modelPath> <maxDepth> <master> [<AppName>]")
            System.err.println("eg: hdfs://192.168.57.104:8020/user/000000_0 10 0.1 spark://192.168.57.104:7077 DecisionTrees")
            System.exit(1)
        }
        val appName = if (args.length > 4) args(4) else "DecisionTrees"
        val conf = new SparkConf().setAppName(appName).setMaster(args(3))
        val sc = new SparkContext(conf)

        val traindata: RDD[LabeledPoint] = MLUtils.loadLabeledPoints(sc, args(0))
        val features = traindata.map(_.features)
        val scaler: StandardScalerModel = new StandardScaler(withMean = true, withStd = true).fit(features)
        val train: RDD[LabeledPoint] = traindata.map(sample => {
            val label = sample.label
            val feature = scaler.transform(sample.features)
            new LabeledPoint(label, feature)
        })
        val splitRdd: Array[RDD[LabeledPoint]] = traindata.randomSplit(Array(1.0, 9.0))
        val testData: RDD[LabeledPoint] = splitRdd(0)
        val realTrainData: RDD[LabeledPoint] = splitRdd(1)

        val boostingStrategy: BoostingStrategy = BoostingStrategy.defaultParams("Classification")
        boostingStrategy.setNumIterations(3)
        boostingStrategy.treeStrategy.setNumClasses(2)
        boostingStrategy.treeStrategy.setMaxDepth(args(2).toInt)
        boostingStrategy.setLearningRate(0.8)
        //  boostingStrategy.treeStrategy.setCategoricalFeaturesInfo(Map[Int, Int]())
        val model = GradientBoostedTrees.train(realTrainData, boostingStrategy)

        val labelAndPreds = testData.map(point => {
            val prediction = model.predict(point.features)
            (point.label, prediction)
        })
        val acc = labelAndPreds.filter(r => r._1 == r._2).count.toDouble / testData.count()

        println("Test Error = " + acc)

        model.save(sc, args(1))
    }
}

设置运行参数

1. E:\IDEA_Projects\mlib\data\GBDT\train E:\IDEA_Projects\mlib\data\GBDT\train\model 10 local