.NET面试题系列[10] - IEnumerable的派生类

.NET面试题系列目录

IEnumerable分为两个版本：泛型的和非泛型的。IEnumerable只有一个方法GetEnumerator。如果你只需要数据而不打算修改它，不打算为集合插入或删除任何成员（例如从远端拿回数据显示），则你不需要任何比IEnumerable更复杂的接口。

ICollection继承IEnumerable。可以使用Count方法统计集合的大小。（注意非泛型版本的ICollection并没有Add，Remove等方法）但在实际情况中，我们通常使用ICollection的继承类而不是ICollection本身（不能初始化一个接口）。ICollection的继承类有Stack，Queue，IDictionary和IList。

IList本身实现了索引器。可以使用[x]来寻找对应元素，还有Add，Remove等方法，可以在任意位置插入和删除成员。

Stack和Queue的使用场景非常典型，就是模拟栈和队列。这两个数据结构继承自ICollection（如果是继承自更下面的例如IList的话，就可以随心所欲的插入和删除成员了），同时实现了特殊的插入删除方法，不需要索引器。对于栈我们只能从最顶拿或者放入数据。对于队列，我们只能从队尾加入数据，从队头取出数据。不过通常，我们都使用栈和队列的泛型版本。

Hashtable

IDictionary继承ICollection，同时，其增加了Add，Remove等方法。可以修改集合的内容。IDictionary的其中一个继承类Hashtable是一个非泛型的集合。其储存着一系列的key Value键值对。这些数据都是Object类型的。

            Hashtable h = new Hashtable {{123, "abc"}, {456, "xyz"}};
            Console.WriteLine(h[123]); //打印abc
            Console.ReadKey();

哈希表查找，插入，删除速度均为O(1)。

哈希（散列）表，哈希函数简介

哈希（散列）表是仅支持插入，删除和查找功能的集合结构。由于实现方式的特殊性，每个哈希表上的元素仅有一个可能出现的位置，就是其哈希函数的值加上冲突之后的调整偏移量，无法移动哈希表上的元素。

哈希表是一种键值对类型的数据结构。它的特点是查找速度飞快，可以达到O(1)的水平。假设你查询的键为x，你可以通过计算一个函数f(x)，获得其值，然后到表中的对应位置获得查询结果。和顺序储存相比，哈希表查找速度快，而顺序储存理论上最快的速度是O(log(n))或O(n)。当数据不连续时，哈希表还能节省空间（相比大数组）。

假设我们有一个全域U={0，1，…，m-1}，假设某应用要用到一个动态集合，其中每个元素都有一个取自全域U的关键字，且没有两个元素具有相同的关键字，那么我们可以建立一个直接寻址表，其中每个位置对应全域的一个关键字。所以这个表将会占有M个位置。一个典型的例子就是员工ID和姓名。我们知道员工的ID一般都是从最小的数字开始一路往上，且不可能有两个员工有相同的ID。如果有10000名员工，我们将员工的姓名储存在一个string[10000]中，就可以根据ID迅速的，以O(1)的速度查找到员工姓名了。

直接寻址表有一个明显的问题：如果实际要存储的关键字比可能的关键字总数小甚至小很多时，大部分表上的空间都浪费了。假设有一个奇葩公司，不停有人辞职，结果开了若干年，ID虽然编到了10000，实际只有100人，则表上9900个位子都是空的，对空间的利用率只有1%。此时，我们就可以考虑用哈希表，在不牺牲插入，删除和查找的速度的同时提高空间利用率。

在直接寻址方式下，具有关键字k的元素被分配到表上的槽k中。在哈希表上具有关键字k的元素则被分配到表上的槽f(k)中，其中f是哈希函数。注意，函数的值和输入变量不一定是一一对应的，例如模函数，19和99模10都是9。如果两个不同的x，却有相同的f(x)值，则意味着当插入时会发生碰撞，这称为哈希冲突。好的哈希函数必须有较少的哈希冲突发生。当然，如果你选择的函数是普通意义上的函数（即一一映射），比如f(x)=x+1，那么永远都不会有冲突发生（因为x是唯一的，没有两个关键字是相同的），但这样一来，哈希表就不能节省空间了。

演示哈希冲突的一个简单例子。我们有10个字符串，哈希函数是将每个字符串字符的ASCII码加总，然后对100取模。我们看到结果只有8个字符串，这是因为发生了冲突，后面的字符串把前面的覆盖掉了。

        static void Main()
        {
            string[] names = new string[99];
            string name;
            string[] someNames = new string[]{"David", "Jennifer", "Donnie", "Mayo", "Raymond", "Bernica", "Mike", "Clayton", "Beata", "Michael"};

            int hashVal;
            for (int i = 0; i < 10; i++)
            {
                name = someNames[i];
                hashVal = SimpleHash(name, names);
                names[hashVal] = name;
            }
            ShowDistrib(names);
            Console.ReadKey();
        }

        static int SimpleHash(string s, string[] arr)
        {
            int tot = 0;
            char[] cname;
            cname = s.ToCharArray();
            for (int i = 0; i <= cname.GetUpperBound(0); i++)
                tot += (int)cname[i];
            return tot % arr.GetUpperBound(0);
        }

        static void ShowDistrib(string[] arr)
        {
            for (int i = 0; i <= arr.GetUpperBound(0); i++)
                if (arr[i] != null)
                    Console.WriteLine(i + " " + arr[i]);
        }

C#中实现了哈希表数据结构的集合类有Hashtable以及它的泛型版本Dictionary<T,K>。Dictionary和Hashtable之间并非只是简单的泛型和非泛型的区别，两者使用了完全不同的哈希冲突解决办法。

在建立哈希表时，确定哈希函数是非常重要的工作。它直接关系到哈希表的插入和查找速度。哈希函数的目标是尽量减少冲突，令元素尽量均匀的分布在哈希表中。但实际应用中冲突是无法避免的，所以在冲突发生时，必须有相应的解决方案。而发生冲突的可能性又跟以下两个因素有关：

（1）装填因子α：所谓装填因子是指表中已存入的记录数n与哈希地址空间大小m的比值，即 α=n / m ，α越小，冲突发生的可能性就越小；α越大（最大可取1），冲突发生的可能性就越大。这很容易理解，因为α越小，哈希表中空闲单元的比例就越大，所以待插入记录同已插入的记录发生冲突的可能性就越小；反之，α越大，哈希表中空闲单元的比例就越小，所以待插入记录同已插入记录冲突的可能性就越大；另一方面，α越小，空间的利用率就越低；反之，空间的利用率就越高。为了既兼顾减少冲突的发生，又兼顾提高存储空间的利用率，通常把α控制在0.6～0.9的范围之内，C#的HashTable类把α的最大值定为0.72，当HashTable中的被占用空间达到72%的时候就将该HashTable自动扩容。例如有一个HashTable的空间大小是100，当它需要添加第73个值的时候将会扩容此HashTable。这个自动扩容的大小是多少呢？答案是当前空间大小的两倍最接近的素数，例如当前HashTable所占空间为素数71，如果扩容，则扩容大小为素数131。

（2）与所采用的哈希函数有关。若哈希函数选择得当，就可使哈希地址尽可能均匀地分布在哈希地址空间上，从而减少冲突的发生；否则，就可能使哈希地址集中于某些区域，从而加大冲突发生的可能性。

冲突解决技术可分为两大类：开散列法（又称为链地址法）和闭散列法（又称为开放地址法）。哈希表是用数组实现的一片连续的地址空间，两种冲突解决技术的区别在于发生冲突的元素是存储在这片数组的空间之外还是空间之内：

（1）开散列法发生冲突的元素存储于数组空间之外。通常会置一链表，然后将元素加到链表中，挂接在原表相应的位置。如果发生冲突，则将链表长度加一，然后将元素放在对应链表的尾端。可以把“开”字理解为需要另外“开辟”空间存储发生冲突的元素。此时如果我们在检索时，计算出关键字的哈希函数值，到相应的表中检查，如果发现表上的关键字和要检索的关键字不同，我们可以顺着后面的链表一路检查下去直到匹配为止。Dictionary<K,T>使用的是这种方式。

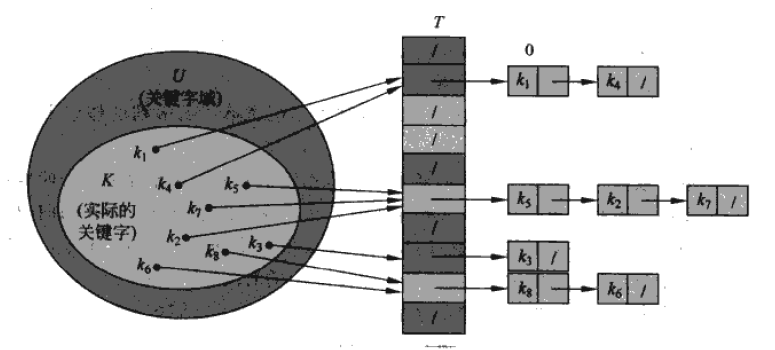
（图片来自算法导论）

（2）闭散列法发生冲突的元素存储于数组空间之内。可以把“闭”字理解为所有元素，不管是否有冲突，都“关闭”于数组之中。闭散列法又称开放寻址法，意指数组空间对所有元素，不管是否冲突都是开放的。此时如果我们在检索时，计算出关键字的哈希函数值，到相应的表中检查，如果发现表上的关键字和要检索的关键字不同，我们可以根据调整策略找到下一个目标位置。当然如果欲插入的元素大于哈希表的大小，则哈希表需要扩容。Hashtable使用的是这种方式。

开放寻址法（闭散列法）

开放寻址法中最自然的方法当然就是看一下相邻的下N个地址是否被占据(N为已经发生冲突的次数)，如果没有就存在那里，如果有就继续探测，直到找到一个空地址为止。这称为线性探测。

线性探测填装一个哈希表的过程：

关键字为{89,18,49,58,69}插入到一个哈希表中的情况。假定取关键字除以10的余数为哈希函数。

散列地址	空表	插入89	插入18	插入49	插入58	插入69
0				49	49	49
1					58	58
2						69
3
4
5
6
7
8			18	18	18	18
9		89	89	89	89	89

 

第一次冲突发生在填装49的时候。地址为9的单元已经填装了89这个关键字，所以往下查找一个单位，发现为空，所以将49填装在地址为0的空单元。第二次冲突则发生在58上，往下查找两个单位，将58填装在地址为1的空单元。69同理。

表的大小选取至关重要，此处选取10作为大小，发生冲突的几率就比选择质数11作为大小的可能性大。越是质数，mod取余就越可能均匀分布在表的各处。

此时如果我们在检索时，计算出关键字的哈希函数值，到相应的表中检查，如果发现表上的关键字和要检索的关键字不同，我们会根据线性探查的特点，查找其后第1，2，3（等等）个数据，直到找到我们要检索的关键字为止。

除了线性探测之外，还有平方探测，它的寻址序列为1，-1，4，-4，9，-9，等等，负数代表向前寻址，不同于线性探测的1，2，3这种尝试数列。

双重哈希法（闭散列法）

HashTable采用开放寻址法中的双重哈希法。这意味着，为哈希表插入元素之后，元素一定会位于表上。所以当插入的元素较多时（例如长度为100的表插入72个元素），插入第73个元素必定会导致扩容。而字典使用的是开散列法，和哈希表不同。

双重哈希法意味着如果出现碰撞，则将本次哈希函数的输出f(x)作为输入再计算一次哈希值y = f(f(x))，如果还有冲突，则采用2y，4y，8y这种尝试数列。显然，f(x)不能为0，否则将导致无限循环，这意味着对于任意的可能输入，哈希函数不能输出0。

哈希表源码：http://referencesource.microsoft.com/#mscorlib/system/collections/hashtable.cs

源码分析：http://blog.csdn.net/exiaojiu/article/details/51206024

自己实现一个哈希表：http://www.cnblogs.com/abatei/archive/2009/06/23/1509790.html#3382887

有兴趣的朋友可以自行研究。

开散列法+使用模函数

Dictionary<K,T>使用这种方式。它的哈希函数是模函数，其中模的底为字典的长度，一般为质数，如果你指定了一个合数作为初始容量则会寻找离他最近的质数作为容量。

若选定的散列表长度为质数m，则可将散列表定义为一个由m个头指针组成的指针数 组T[0..m-1]。凡是散列地址为i的结点，均插入到以T[i]为头指针的单链表中。T中各分量的初值均为空指针。

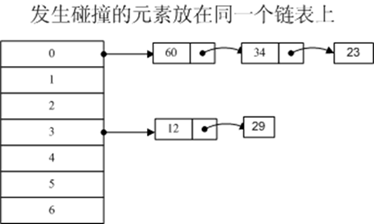
链表的长度不算在字典的空间内。上图如果只有两个位置被占据（例如0和3），则即使它们后面的链表有一万个元素，字典也不会扩容。只有头指针被占据的数目过多才会扩容。如果字典的头指针被占用空间达到72%的时候就自动扩容。其扩容后的新容量为最接近原来容量2倍的质数。

C#字典的源码：http://referencesource.microsoft.com/#mscorlib/system/collections/generic/dictionary.cs

源码分析：http://blog.csdn.net/exiaojiu/article/details/51252515

有兴趣的朋友可以自行研究。

模函数底的取值

如果哈希函数是形如n (mod m)的模函数，则m的取值有以下几个注意事项。

M不能为2的幂。对于任何二进制数字，他们对2的幂取模造成了信息的丢弃。算法导论是这样解释的：对一个数除以2^p取余数相当于只取这个数的最低的p位，高于p位的信息就被丢弃了。

这个原理很容易理解：假设m=8，则p=3。15的二进制表示1111，8的二进制表示1000，取模之后余数为7，二进制表示是111，即k的最低3位。23的二进制表示是10111，对8的余数仍然为7，这样相当于不管k的除去最后3位取什么值，结果都是不变的（只取这个数的最低的p位）。

M最好取一个素数。理论上，可以在输入并非均匀分布时降低碰撞的发生次数。（如果输入是均匀分布的则M取什么数都可以）理由我没有看懂，敬请大牛指导：http://thuhak.blog.51cto.com/2891595/1352903

ArrayList

数组是C#中最基础的一种数据类型，它代表一块连续的内存，一旦初始化之后，容量便已经确定。若想要动态扩充容量，那么动态数组可以满足这点需求。ArrayList是C#最不常用（我想不出任何用它的理由）也是最基础的一个动态数组。

通常我们在说ArrayList时，总是和List<T>和普通的数组（无法扩容）进行比较。ArrayList派生自IList，所以其是一个非泛型的集合。IList继承ICollection，同时，其增加了Add，Remove等方法。可以修改集合的内容。它的缺点在于里面的成员都是Object类型的，故会影响性能，还造成类型不安全。

ArrayList的容量不定。如果元素超过容量，则通过倍增的方式扩容。

ArrayList内部是通过数组实现的。查找速度为O(N)，插入删除速度为O(N)。ArrayList操作可能会导致装箱和拆箱，几乎永远不会被使用。

IEnumerable的派生类：小结

	访问特定位置的成员方式	继承自	特点
IEnumerable	通过ElementAt	无	有泛型版本 提供遍历（通过GetEnumerator) 不能实例化（所有接口都是如此）
ICollection	通过ElementAt	IEnumerable	有泛型版本 提供Count方法 提供转换为IQueryable方法
ArrayList	索引器	IList	dynamic sized,大小倍增 弱类型（所有的成员被视作object） 对应的泛型版本为List<T> 不使用
HashTable	键值对	IDictionary	dynamic sized,扩容通过寻找倍增之后最近的质数确定容量 弱类型（所有的成员被视作object）， 对应的泛型版本为Dictionary<T,K>
Stack	无	ICollection	栈的实现,不使用
Queue	无	ICollection	队列的实现,不使用