树状数组

看到树状数组后觉得这个数据结构很优美，比较有意思，虽然很多时候线段树能做，但树状数组内存消耗更小，思想也很有意思，就想记录一下

 

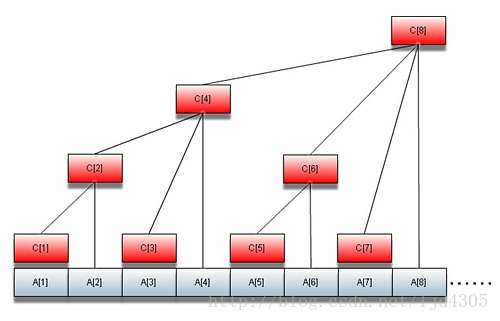
 看上去是比较漂亮的，A[] 是序列的实际数值， C[] 记录的是某一段A[]的和，例如 C[4]就是 sun(1--4)。

先介绍个很关键的函数：int lowbit(int x){return x&(-x);} 这个可以返回二进制数 x 中最低位的 1 还是 1 ，其余都为 0 的数,比如对于 1000(8的二进制) 1000=100+lowbit(100)=110+lowbit(110)=111+lowbit(111);

其实 C[i] 有很多性质:

1，将 i 化为二进制，比如 i = 6 = 110 那么 lowbit(6) = 2 ，代表 C[6] 记录了 2 个数的和, lowbit(7)=1 ,所以 C[7] 记录的 1 个数的和，所以查询时 i-lowbit(i) 会到 C[i] 恰好没覆盖到的地方

2，C[i]的父节点是 C[i+lowbit(i)]，也就是说，i+lowbit(i) 是记录了 i 记录的前缀和的，所以更新时要不断向父节点更新。

看懂了这些再看看代码，很容易理解了

 求区间和O(log n)，便于单点更新，区间查询:

#include <iostream>
#include <stdio.h>
#include <string.h>

using namespace std;
#define MAXN 1000

int n;
int A[MAXN];
int C[MAXN];

int lowbit(int x)
{
    return x&(-x);
}

void update(int x,int add) //A[x]增减
{
    while (x<=n)
    {
        C[x]+=add;
        x+=lowbit(x);
    }
}

void new_tree(int n)   //建树,直接利用update
{
    memset(C,0,sizeof(C));
    for (int i=1;i<=n;i++)
        update(i,A[i]);
}

int getsum(int x)//[1--x]的和
{
    int sum=0;
    while(x>0)
    {
        sum+=C[x];
        x -= lowbit(x); //性质1
    }
    return sum;
}

int main()
{
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
        scanf("%d",&A[i]);
    new_tree(n);

    int l,r;
    scanf("%d %d",&l,&r);
    printf("%d\n",getsum(r)-getsum(l-1)); //l--r 的和

    return 0;
}

 虽然用前缀和求区间和是O(1)，但是不便更新

 

树状数组还可以很方便的做区间更新，单点查询，更新时 update(L,v),update(R+1,-v) ，查询为 get_sum(i)， 即可，还是因为树状数组保存的是前缀和的原因

 

 还可以升级到多维的，很厉害