最短路径算法——Dijkstra and Floyd算法
最短路径算法——Dijkstra算法
Dijkstra算法在刚开始在学数据结构的时候,完全没弄明白,主要是也不怎么想去弄明白。而从学校出来到现在,最短路径算法都没有实际运用过,最近在一个GIS项目中总算用到了,于是乎把教材重温了下,同时查阅了网上一些资料,借鉴了一些别人的东西,并顺利用写进了项目中,文中的主要代码来自于园子里的一位大哥,这位大哥对通用框架的研究很深入,他的链接为:http://zhuweisky.cnblogs.com/archive/2005/09/29/246677.html(最短路径)。另外,文章的最后面的一些链接是我找资料的时候用到过的,有兴趣
的朋友可以去看看。
最短路径分析在事故抢修、交通指挥、GPS导航等行业应用中使用的非常广泛, 以至于大多数GIS平台都会把这个分析功能作为一个最基础的功能集成进去,如ARCGIS,SuperMap等。个人感觉想要了解这个算法的来龙去脉,一方面是参与相关书籍仔细理解,另外一个最重要的是要去调试代码。由于历史原因,对于书上的伪C代码,我是完全不感兴趣的,而且由于有严格的数学证明,所以看起来相对较难,而对于面向对象实现的算法,我很感兴趣,也感觉很容易理解,所以一边针对C#实现的面向对象代码再一边对照书籍,感觉理解的层次就加深了。
Dijkstra算法又称为单源最短路径,所谓单源是在一个有向图中,从一个顶点出发,求该顶点至所有可到达顶点的最短路径问题。要顺利实现算法,要求理解Dijstra的算法,同时还要理解图的一些基本概念,图由节点和边构成,将节点和边看成对象,每个对象有自己的特有属性,如在GIS中,一个节点必须都有ID,横坐标,纵坐标等基本属性,边有起点节点,终点节点,长度等属性,而最短路径分析,就是根据边的长度(权值)进行分析的。
边的定义如下:
{
public string StartNodeID;
public string EndNodeID;
public double Weight; //权值,代价
}
节点的定义:
{
private string iD ;
private List<Edge> edgeList ;//Edge的集合--出边表
public Node(string id )
{
this.iD = id ;
this.edgeList = new List<Edge>() ;
}
#region property
public string ID
{
get
{
return this.iD ;
}
}
public List<Edge> EdgeList
{
get
{
return this.edgeList ;
}
}
#endregion
}
本次用于分析的拓扑图如下:(A为起点,D为终点,边上的数字为权值)
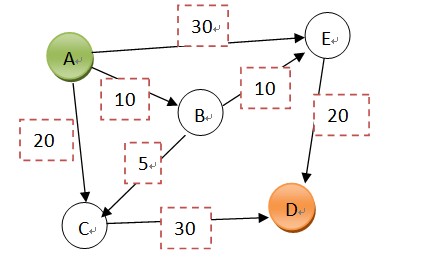
利用上述的边与节点的定义,可以通过代码简单的构成如下图:
{
public List<Node> m_nodeList = null;
public Graph()
{
m_nodeList = new List<Node>();
}
/// <summary>
/// 获取图的节点集合
/// </summary>
public List<Node> NodeList
{
get { return this.m_nodeList; }
}
/// <summary>
/// 初始化拓扑图
/// </summary>
public void Init()
{
//***************** B Node *******************
Node aNode = new Node("A");
m_nodeList.Add(aNode);
//A -> B
Edge aEdge1 = new Edge();
aEdge1.StartNodeID = aNode.ID;
aEdge1.EndNodeID = "B";
aEdge1.Weight = 10;
aNode.EdgeList.Add(aEdge1);
//A -> C
Edge aEdge2 = new Edge();
aEdge2.StartNodeID = aNode.ID;
aEdge2.EndNodeID = "C";
aEdge2.Weight = 20;
aNode.EdgeList.Add(aEdge2);
//A -> E
Edge aEdge3 = new Edge();
aEdge3.StartNodeID = aNode.ID;
aEdge3.EndNodeID = "E";
aEdge3.Weight = 30;
aNode.EdgeList.Add(aEdge3);
//***************** B Node *******************
Node bNode = new Node("B");
m_nodeList.Add(bNode);
//B -> C
Edge bEdge1 = new Edge();
bEdge1.StartNodeID = bNode.ID;
bEdge1.EndNodeID = "C";
bEdge1.Weight = 5;
bNode.EdgeList.Add(bEdge1);
//B -> E
Edge bEdge2 = new Edge();
bEdge2.StartNodeID = bNode.ID;
bEdge2.EndNodeID = "E";
bEdge2.Weight = 10;
bNode.EdgeList.Add(bEdge2);
//***************** C Node *******************
Node cNode = new Node("C");
m_nodeList.Add(cNode);
//C -> D
Edge cEdge1 = new Edge();
cEdge1.StartNodeID = cNode.ID;
cEdge1.EndNodeID = "D";
cEdge1.Weight = 30;
cNode.EdgeList.Add(cEdge1);
//***************** D Node *******************
Node dNode = new Node("D");
m_nodeList.Add(dNode);
//***************** E Node *******************
Node eNode = new Node("E");
m_nodeList.Add(eNode);
//E -> D
Edge eEdge1 = new Edge();
eEdge1.StartNodeID = eNode.ID;
eEdge1.EndNodeID = "D";
eEdge1.Weight = 20;
eNode.EdgeList.Add(eEdge1);
}
}
有了拓扑节点和边,就可以根据算法构造其他最短路径分析的对象了,主要步骤如下:
Ø 初始化图中的从A出发的路径集合:
/// PlanCourse 缓存从源节点到其它任一节点的最小权值路径(路径表)
/// </summary>
public class PlanCourse
{
private Hashtable htPassedPath;
#region ctor
public PlanCourse(List<Node> nodeList, string originID)
{
this.htPassedPath = new Hashtable();
Node originNode = null;
foreach (Node node in nodeList)
{
if (node.ID == originID)
{
originNode = node;
}
else
{
PassedPath pPath = new PassedPath(node.ID);
this.htPassedPath.Add(node.ID, pPath);
}
}
if (originNode == null)
{
throw new Exception("The origin node is not exist !");
}
this.InitializeWeight(originNode);
}
/// <summary>
/// 通过指定节点的边的权值初始化路径表
/// </summary>
/// <param name="originNode"></param>
private void InitializeWeight(Node originNode)
{
if ((originNode.EdgeList == null) || (originNode.EdgeList.Count == 0))
{
return;
}
foreach (Edge edge in originNode.EdgeList)
{
PassedPath pPath = this[edge.EndNodeID];
if (pPath == null)
{
continue;
}
pPath.PassedIDList.Add(originNode.ID);
pPath.Weight = edge.Weight;
}
}
#endregion
/// <summary>
/// 获取指定点的路径表
/// </summary>
/// <param name="nodeID"></param>
/// <returns></returns>
public PassedPath this[string nodeID]
{
get
{
return (PassedPath)this.htPassedPath[nodeID];
}
}
}
Ø 从A中最短路径集合中找到一个最短的路径点Vi开始分析
/// 从PlanCourse取出一个当前累积权值最小,并且没有被处理过的节点
/// </summary>
/// <returns></returns>
private Node GetMinWeightRudeNode(PlanCourse planCourse, List<Node> nodeList, string originID)
{
double weight = double.MaxValue;
Node destNode = null;
foreach (Node node in nodeList)
{
if (node.ID == originID)
{
continue;
}
PassedPath pPath = planCourse[node.ID];
if (pPath.BeProcessed)
{
continue;
}
if (pPath.Weight < weight)
{
weight = pPath.Weight;
destNode = node;
}
}
return destNode;
}
Ø 修正从A出发至Vi最短路径,并重新选择另一个最短路径点Vj点开始分析,重新执行上述步骤的路径分析
{
PassedPath curPath = planCourse[curNode.ID];
foreach (Edge edge in curNode.EdgeList)
{
PassedPath targetPath = planCourse[edge.EndNodeID];
double tempWeight = curPath.Weight + edge.Weight;
if (tempWeight < targetPath.Weight)
{
targetPath.Weight = tempWeight;
targetPath.PassedIDList.Clear();
for (int i = 0; i < curPath.PassedIDList.Count; i++)
{
targetPath.PassedIDList.Add(curPath.PassedIDList[i].ToString());
}
targetPath.PassedIDList.Add(curNode.ID);
}
}
//标志为已处理
planCourse[curNode.ID].BeProcessed = true;
//获取下一个未处理节点
curNode = this.GetMinWeightRudeNode(planCourse, nodeList, originID);
}
Ø 重复上述两个步骤,一直到所有的对象都分析完为止。
Ø 这个时候的路径集合表中已经保存了从A到任意一点的最短路径集合了。
/// 从PlanCourse表中取出目标节点的PassedPath,这个PassedPath即是规划结果
/// </summary>
/// <returns></returns>
private RoutePlanResult GetResult(PlanCourse planCourse, string destID)
{
PassedPath pPath = planCourse[destID];
if (pPath.Weight == int.MaxValue)
{
RoutePlanResult result1 = new RoutePlanResult(null, int.MaxValue);
return result1;
}
string[] passedNodeIDs = new string[pPath.PassedIDList.Count];
for (int i = 0; i < passedNodeIDs.Length; i++)
{
passedNodeIDs[i] = pPath.PassedIDList[i].ToString();
}
RoutePlanResult result = new RoutePlanResult(passedNodeIDs, pPath.Weight);
return result;
}
最短路径的结果类定义如下:
{
public RoutePlanResult(string[] passedNodes, double value)
{
m_resultNodes = passedNodes;
m_value = value;
}
private string[] m_resultNodes;
/// <summary>
/// 最短路径经过的节点
/// </summary>
public string[] ResultNodes
{
get { return m_resultNodes; }
}
private double m_value;
/// <summary>
/// 最短路径的值
/// </summary>
private double Value
{
get { return m_value; }
}
}
Demo下载:最短路径分析demo
其他技术文章链接:
1. Dijkstra算法http://www.cnblogs.com/gzydn/archive/2009/07/09/1520019.html
2.最短路径 dijsktra 模板 http://www.cnblogs.com/yezizhe/archive/2009/04/16/1437062.html
3. Shortest Path Problem: Dijkstra's Algorithm http://www.codeproject.com/KB/recipes/Shortest_Path_Problem.aspx
4. Dijkstra:Shortest Route Calculation - Object Oriented
http://www.codeproject.com/KB/recipes/ShortestPathCalculation.aspx
5.推荐:路径规划(最短路径)算法C#实现http://zhuweisky.cnblogs.com/archive/2005/09/29/246677.html
6.【Floyd最短路径算法http://www.cnblogs.com/gzydn/archive/2009/07/10/1520646.html
7.【最短路径算法及应用】
http://blog.csdn.net/baggioan/archive/2007/07/28/1713294.aspx


