20162306 2017-2018-1《程序设计与数据结构》 第9周学习总结
20162306 2017-2018-1《程序设计与数据结构》 第9周学习总结
教材学习内容总结
-
1、 堆:堆是一棵完全二叉树,其中每个元素都大于等于其所有子结点的值。
-
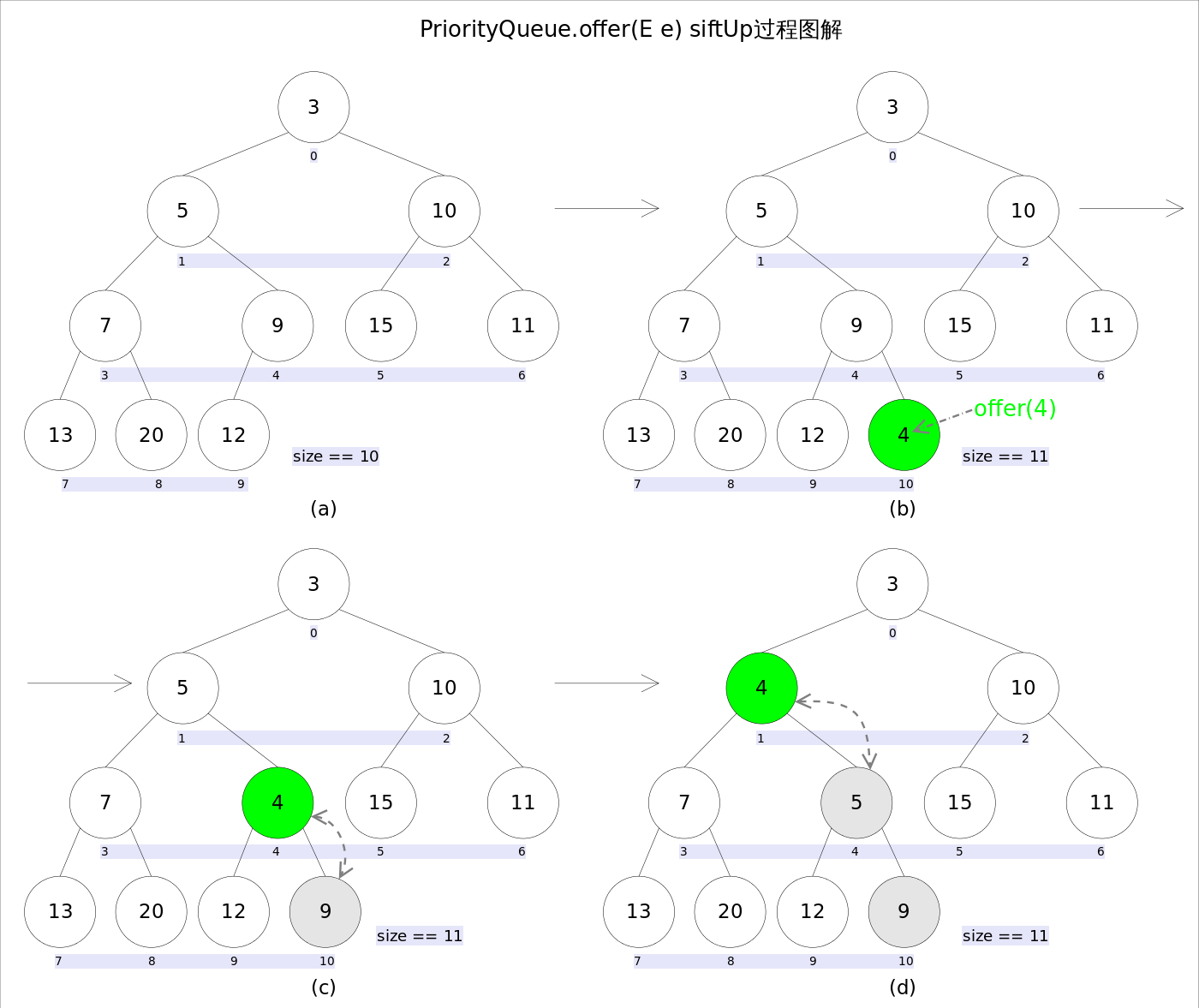
2、向堆中添加一个元素
(1)首先将这个元素添加为叶结点,然后将其向上移动到合适的位置; -
3、从堆中删除最大元素
(1)利用最后的叶结点来取代根,然后将其向下移动到合适的位置; -
4、堆的排序
(1)堆排序利用堆的基本特性对一组元素进行排序; -
5、优先队列
(1)优先队列不是FIFO队列。他根据优先级排列元素,而不是根据他们进入队列的次序来排序;
教材学习中的问题和解决过程
- 问题1:课上的活动“说明堆与二叉排序树的差别”课上没有太理解,课下又查阅了一些资料,做了进一步的拓展。
- 问题1解决方案:
在二叉排序树中,每个结点的值均大于其左子树上所有结点的值,小于其右子树上所有结点的值,对二叉排序树进行中序遍历得到一个有序序列。所以,二叉排序树是结点之间满足一定次序关系的二叉树;
堆是一个完全二叉树,并且每个结点的值都大于或等于其左右孩子结点的值(这里的讨论以大根堆为例),所以,堆是结点之间满足一定次序关系的完全二叉树。
具有n个结点的二叉排序树,其深度取决于给定集合的初始排列顺序,最好情况下其深度为log n(表示以2为底的对数),最坏情况下其深度为n;
具有n个结点的堆,其深度即为堆所对应的完全二叉树的深度log n 。
在二叉排序树中,某结点的右孩子结点的值一定大于该结点的左孩子结点的值;在堆中却不一定,堆只是限定了某结点的值大于(或小于)其左右孩子结点的值,但没有限定左右孩子结点之间的大小关系。
在二叉排序树中,最小值结点是最左下结点,其左指针为空;最大值结点是最右下结点,其右指针为空。在大根堆中,最小值结点位于某个叶子结点,而最大值结点是大根堆的堆顶(即根结点)。
二叉排序树是为了实现动态查找而设计的数据结构,它是面向查找操作的,在二叉排序树中查找一个结点的平均时间复杂度是O(log n);
堆是为了实现排序而设计的一种数据结构,它不是面向查找操作的,因而在堆中查找一个结点需要进行遍历,其平均时间复杂度是O(n)。
- 问题2:对教材18.4节优先队列的相关知识进行了一些深入了解。
- 问题2解决方案:上网查阅博客,结合图例和代码了解到:
优先队列:顾名思义,首先它是一个队列,但是它强调了“优先”二字,所以,已经不能算是一般意义上的队列了,它的“优先”意指取队首元素时,有一定的选择性,即根据元素的属性选择某一项值最优的出队~
优先级队列 是不同于先进先出队列的另一种队列。每次从队列中取出的是具有最高优先权的元素
优先队列的类定义
优先队列是0个或多个元素的集合,每个元素都有一个优先权或值,对优先队列执行的操作有1) 查找;
- 插入一个新元素;
- 删除.在最小优先队列(min priorityqueue)中,查找操作用来搜索优先权最小的元素,删除操作用来删除该元素;对于最大优先队列(max priority queue),查找操作用来搜索优先权最大的元素,删除操作用来删除该元素.优先权队列中的元素可以有相同的优先权,查找与删除操作可根据任意优先权进行.

代码调试中的问题和解决过程
- 问题1:教材410页18.4的代码调试出了问题,两个方法不能实现。
- 问题1解决方案:贴心的课代表在班群里发了要将addElement方法改为add方法,同时将removeMin改为removeMax;
上面的问题解决后又发现PriorityQueueNode类实现了Comparable接口,用到了泛型,把比较的类型设为PriorityQueueNode类型时,漏了一个。
代码托管
结对及互评
- 博客中值得学习的或问题:
- 对于教材代码研究的很透彻
本周结对学习情况
[20162305](http://www.cnblogs.com/lyxwatm/p/7710984.html)
- 结对学习内容
- 梳理教材内容
- 理解课上内容
其他(感悟、思考等,可选)
- 树和堆的内容都讲了之后发现有一点混乱。。。。要找时间把这两部分内容梳理一下,
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 10/10 | |
| 第二、三周 | 303/303 | 2/3 | 10/20 | |
| 第四、五、六周 | 700/1003 | 2/5 | 10/20 | |
| 第七周 | 663/1666 | 1/6 | 15/35 | |
| 第八、九周 | 754/2420 | 2/8 | 19/54 |
-
计划学习时间:20小时
-
实际学习时间:19小时




 浙公网安备 33010602011771号
浙公网安备 33010602011771号