刷题
面试题1:赋值运算符函数
题目:如下为类型CMyString的声明,请为该类型添加赋值运算符函数。
class CMyString
{
public:
CMyString(char* pData = NULL);
CMyString(const CMyString& str);
~CMyString(void);
private:
char* m_pData;
};
解析:先利用传进来的参数str创建一个临时实例temp,接着把temp.m_pData和实例自身的m_pData做交换。由于temp是一个局部变量,当程序运行到if外面时也就出了该变量的作用域,就会自动调用temp的析构函数,把temp.m_pData所指向的内存释放掉。又因为temp.m_pData已经指向实例之前m_pData的内存,这就相当于释放了实例之前的内存,那么现在实例的m_pData也指向了str的m_pData,完成了运算符重载。
1 CMyString& CMyString::operator=(const CMyString& str) 2 { 3 if (this != &str) 4 { 5 CMyString temp(str); 6 7 char* data = temp.m_pData; 8 temp.m_pData = this->m_pData; 9 this->m_pData = data; 10 } 11 12 return *this; 13 } 14
面试题2:二维数组中的查找
题目:在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
解析:首先选取一个角上的数字进行比较,这里我选择了右上角,可通过比较大小缩小查找的区域范围,找到则返回true,没找到返回false。例如:
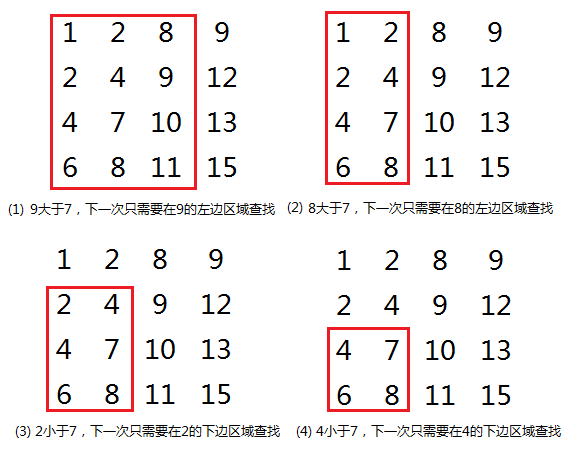
1 bool Find(int* array, int rows, int columns, int number) 2 { 3 assert(array); 4 5 if (array!=NULL && rows > 0 && columns > 0) 6 { 7 int row = 0; 8 int col = columns - 1; 9 while (row < rows && col >= 0) 10 { 11 if (array[row*columns + col] == number) 12 { 13 return true; 14 } 15 else if (array[row*columns + col] > number) 16 { 17 --col; 18 } 19 else 20 { 21 ++row; 22 } 23 } 24 } 25 26 return false; 27 }
面试题3:替换空格
题目:请实现一个函数,把字符串中的每个空格替换成“%20”。例如输入“We are happy.”,则输出“We%20are%20happy.”。
解析:首先遍历一次字符串,统计空格数目,计算出替换之后的字符串长度。接着准备两个指针P1、P2,P1指向原字符串末尾,P2指向新字符串末尾,从后往前移动,遇到字符则复制,遇到空格则替换。
1 //length为字符数组str的总容量
2 void ReplaceBlank(char str[], int length)
3 {
4 if (str == NULL && length <= 0)
5 {
6 return;
7 }
8
9 //originalLen为字符串str的实际长度,numberOfBlank是空格数目
10 int originalLen = 0;
11 int numberOfBlank = 0;
12 int i = 0;
13 while (str[i] != '\0')
14 {
15 ++originalLen;
16 if (str[i] == ' ')
17 {
18 ++numberOfBlank;
19 }
20
21 ++i;
22 }
23
24 //newLen是新字符串的长度
25 int newLen = originalLen + numberOfBlank * 2;
26 if (newLen > length)
27 {
28 return;
29 }
30 int originalIndex = originalLen;
31 int newIndex = newLen;
32 while (originalIndex >= 0 && newIndex > originalIndex)
33 {
34 if (str[originalIndex] == ' ')
35 {
36 str[newIndex--] = '0';
37 str[newIndex--] = '2';
38 str[newIndex--] = '%';
39 }
40 else
41 {
42 str[newIndex--] = str[originalIndex];
43 }
44 --originalIndex;
45 }
46 }
面试题4:从尾到头打印链表
题目:输入一个链表的头结点,从尾到头反过来打印出每个节点的值。
链表节点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
解析:可以用递归的思想。每访问到一个节点的时候,先递归输出它后面的节点,在输出该节点自身,这样链表的输出结果就反过来了。
1 void PrintTailToHead(ListNode * pHead)
2 {
3 if (pHead)
4 {
5 PrintTailToHead(pHead->m_pNext);
6 printf("%d <- ", pHead->m_nKey);
7 }
8 }
面试题5:重建二叉树
题目:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建出如图的二叉树并输出它的头节点。二叉树节点的定义如下:
struct BinaryTreeNode
{
int _data;
BinaryTreeNode* _left;
BinaryTreeNode* _right;
};

解析:根据前序遍历和中序遍历的特点,可以发现,前序遍历的每一个节点,都是当前子树的根节点,同时以对应的节点为边界,就会把中序遍历的结果分为左子树和右子树。
前序:1,2,4,7,3,5,6,8
中序:4,7,2,1,5,3,8,6
“1”是前序遍历节点中的第一个元素,它把中序遍历的结果分成“4,7,2”和“5,3,8,6”两个部分,即“1”的左右子树的遍历结果。找到前序遍历中对应的左右子树,就可以把“1”作为当前的根节点,然后依次递归下去,把左右子树的遍历结果也依次恢复出来。
1 void ReBuild(char* PreOrder, char* InOrder, int TreeLen, BinaryTreeNode*& root) 2 { 3 //检查边界条件 4 if (PreOrder == NULL || InOrder == NULL) 5 return; 6 7 //获得前序遍历的第一个节点 8 BinaryTreeNode* temp = new BinaryTreeNode; 9 temp->_data = *PreOrder; 10 temp->_left = NULL; 11 temp->_right = NULL; 12 13 //如果节点为空,把当前节点复制到根节点 14 if (root == NULL) 15 root = temp; 16 17 //如果当前树长度为1,那么已经是最后一个节点 18 if (TreeLen == 1) 19 return; 20 21 22 //寻找子树长度 23 char* pOrgInOrder = InOrder; 24 char* pLeftEnd = InOrder; 25 int templen = 0; 26 27 //找到左子树的结尾 28 while (*PreOrder != *pLeftEnd) 29 { 30 if (PreOrder == NULL || pLeftEnd == NULL) 31 { 32 return; 33 } 34 templen++; 35 36 //记录临时长度,以免溢出 37 if (templen > TreeLen) 38 { 39 break; 40 } 41 pLeftEnd++; 42 } 43 44 //寻找左子树长度 45 int LeftLen = 0; 46 LeftLen = (int)(pLeftEnd - pOrgInOrder); 47 48 //寻找右子树长度 49 int RightLen = 0; 50 RightLen = TreeLen - LeftLen - 1; 51 52 //重建左子树 53 if (LeftLen > 0) 54 { 55 ReBuild(PreOrder + 1, InOrder, LeftLen, ((root)->_left)); 56 } 57 58 //重建右子树 59 if (RightLen > 0) 60 { 61 ReBuild(PreOrder + LeftLen + 1, InOrder + LeftLen + 1, 62 RightLen, ((root)->_right)); 63 } 64 }
题目:用两个栈实现一个队列。队列的声明如下,请实现它的两个函数appendTail和deleteHead,分别完成在队列尾部插入节点和在队列头部删除节点的功能。
template<typename T>
class CQueue
{
public:
CQueue(void);
~CQueue(void);
void appendTail(const T& node);
T deleteHead();
private:
stack<T> stack1;
stack<T> stack2;
};
解析:用两个“后进先出”的栈实现一个“先进先出”的队列。有这样一种方法,令s1用来入栈,s2用来出栈。入队列时,压入s1中,出队列时,先把s1中的元素全部出栈压入s2中,在弹出s2的栈顶元素就可以了。
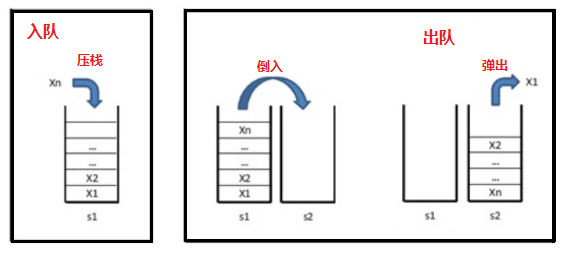
1 template<typename T> 2 void CQueue<T>::appendTail(const T& x) 3 { 4 stack1.push(x); 5 } 6 7 template<typename T> 8 T CQueue<T>::deleteHead() 9 { 10 if (stack2.size() <= 0) 11 { 12 while (stack1.size() > 0) 13 { 14 T& data = stack1.top(); 15 stack1.pop(); 16 stack2.push(data); 17 } 18 } 19 20 if (stack2.size() == 0) 21 { 22 cout << "The queue is empty." << endl; 23 } 24 25 T head = stack2.top(); 26 stack2.pop(); 27 28 return head; 29 }
面试题7:旋转数组的最小数字
题目:把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
解析:旋转之后的数组可以划分为两个排序的子数组,而且前面的子数组的元素都大于或者等于后面子数组的元素。最小的元素刚好是这两个子数组的分界线。在排序的数组中可以用二分查找。用两个指针分别指向数组的第一个元素和最后一个元素,当中间元素位于前面的递增数组,那么它应该大于或者等于第一个指针指向的元素,此时最小元素应该在中间元素的后面,可以把第一个指针指向该中间元素,缩小范围;同样,如果中间元素位于后面的递增子数组,它应该小于或者等于第二个指针指向的元素,最小元素位于中间元素的前面,可以把第二个指针指向该中间元素,缩小范围。重复查找知道找到最小。
1 int FindMin(int* array, int length) 2 { 3 if (array == NULL || length <= 0) 4 { 5 cout << "Invalid" << endl; 6 7 } 8 9 int left = 0; 10 int right = length - 1; 11 int mid = left; 12 while (array[left] >= array[right]) 13 { 14 if (right - left == 1) 15 { 16 mid = right; 17 break; 18 } 19 20 mid = left + (right - left) / 2; 21 if (array[mid] >= array[left]) 22 { 23 left = mid; 24 } 25 else if (array[mid] <= array[right]) 26 { 27 right = mid; 28 } 29 } 30 return array[mid]; 31 }




