EM算法 学习笔记
转载请注明出处: http://www.cnblogs.com/gufeiyang
首先考虑这么一个问题。操场东边有100个男生，他们的身高符合高斯分布。操场西边有100个女生，她们的身高也符合高斯分布。 如果告诉了男生的身高，我们很容易用极大似然估计求出正态分布的参数。 同理，给出了女生的身高，我们也很容易得到高斯分布的参数。 接下来事情发生了， 男生跑入女生队伍中， 然后统计了200个人的身高，但是却不知道每个身高是男的还是女生的。 这样的话就很纠结了。 如果我们要是知道了每个人的性别改多好啊， 知道了性别就可以用极大似然得到两个高斯分布的参数了。 如果我们知道了高斯分布的参数，那么我就可以估计出来每个身高属于男女的概率。 忽然间我们发现这是一个“先有鸡还是先有蛋” 的问题。
EM算法基本思想：假设我们想估计的参数为A，B。 开始的时候A和B都未知， 但是如果我们知道了A，就能得到B。 我们得到了B就可以得到A。 EM会给A一个初始值，然后得到B，再由B得到A， 再得到B，一直迭代到收敛为止。
说完了EM算法的基本思想， 下面我讲详细介绍EM算法的公式推导。
现在有样本集 X1,X2......Xm, 一共m个样本， 每个样本都有一个隐变量Zi,但是这个变量却不知道（隐变量嘛）。 我们需要估计的概率模型为P(X|Z)的参数θ。针对上一个例子，X为身高，Z给男女，θ为高斯分布的参数。
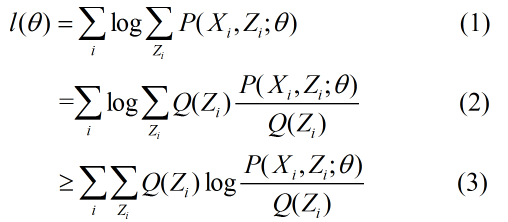
由于函数 f(x)=log(x)是一个凹函数，所有(2)式到(3)式可以利用jeson不等式。 其实l(θ)使我们的目标函数(如果Zi确定的话).我们这个时间找到了l(θ)的下界。 我们可以调整θ,然后再极大化下界，再调整θ......一直迭代到收敛为止。
这个时候我们不禁会想两个问题。 (a)上边 的推导中用了不等号，什么时间可以取等号呢？ (b)真的一定会收敛吗？
我们先讨论第一个问题，由于 
,( Q(Zi)是Zi的概率密度函数)，当
为常数时， 不等式就变成了等式。我们令这个常数为
，那么
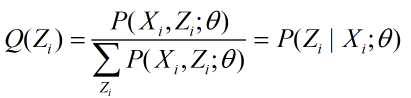
我们在给定了参数θ后，使下界拉升的Q(Zi)就能计算了。 给定了Q(Zi)后，又能调整θ,接着极大化新θ的下界......
因此EM算法的步骤为：
E步骤：根据参数初始值或上一次迭代的模型参数计算隐变量的后验概率：
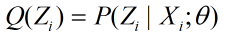
M步骤：将似然函数极大化，以获得新的参数值:
一直重复这两个步骤。
接着讨论第二个问题：这样的迭代会收敛吗？
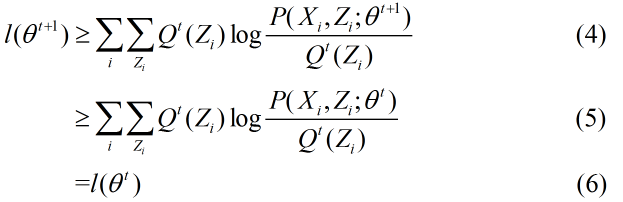
从上边的推到来看，EM算法是收敛的。具体推导参看 Andrew Ng《The EM algorithm》。
至此EM算法就介绍完了。 需要指出EM算法不能保证全局最优。不同的初始值， 得到最后的结果可能不一样。
参考资料：
《统计学习方法》 李航著
zouxy09博客 http://blog.csdn.net/zouxy09/article/details/8537620
