伸展树

伸展树(Splay Tree)树平衡二叉查找树的一种，具有二叉查找树的所有性质。在性能上又比普通的二叉查找树有所改进：普通的二叉查找树在最坏情况下的查找操作的时间复杂度为O(n)（当二叉树退化成一条链的时候），而伸展树在任何情况下的平摊时间复杂度均为 O(log2n).

特性

1. 和普通的二叉查找树相比，具有任何情况下、任何操作的平摊O(log2n)的复杂度，时间性能上更好
2. 和一般的平衡二叉树比如 红黑树、AVL树相比，维护更少的节点额外信息，空间性能更优，同时编程复杂度更低
3. 在很多情况下，对于查找操作，后面的查询和之前的查询有很大的相关性。这样每次查询操作将被查到的节点旋转到树的根节点位置，这样下次查询操作可以很快的完成
4. 可以完成对区间的查询、修改、删除等操作，可以实现线段树和树状数组的所有功能 
    

旋转

    伸展树实现O(log2n)量级的平摊复杂度依靠每次对伸展树进行查询、修改、删除操作之后，都进行旋转操作 Splay(x, root)，该操作将节点x旋转到树的根部。 
    伸展树的旋转有六种类型，如果去掉镜像的重复，则为三种：zig(zag)、zig-zig(zag-zag)、zig-zag(zag-zig)。

1 自底向上的方式进行旋转

    这种方式需要每个节点存放其父节点的指

1.1 zig旋转

 
    如图所示，x节点的父节点为y，x为y的左子节点，且y节点为根。则只需要对x节点进行一次右旋(zig操作)，使之成为y的父节点，就可以使x成为伸展树的根节点。

1.2 zig-zig旋转

 
    如上图所示，x节点的父节点y，y的父节点z，三者在一字型链上。此时，先对y节点和z节点进行zig旋转，然后再对x节点和y节点进行zig旋转，最后变为右图所示，x成为y和z的祖先节点。

1.3 zig-zag旋转

 
    如上图所示，x节点的父节点y，y的父节点z，三者在之字型链上。此时，先对x节点和y节点进行zig旋转，然后再对x节点和y节点进行zag旋转，最后变为右图所示，x成为y和z的祖先节点。

2 自顶向下的方式进行旋转

    这种方式不需要节点存储其父节点的指针。当我们沿着树向下搜索某个节点x时，将搜索路径上的节点及其子树移走。构建两棵临时的树——左树和右树。没有被移走的节点构成的树称为中树。

(1) 当前节点x是中树的根 
(2) 左树L保存小于x的节点 
(3) 右树R保存大于x的节点

    开始时候，x是树T的根，左树L和右树R都为空。三种旋转操作：

2.1 zig旋转

 
    如图所示，x节点的子节点y就是我们要找的节点，则只需要对y节点进行一次右旋(zig操作)，使之成为x的父节点，就可以使y成为伸展树的根节点。将y作为中树的根，同时，x节点移动到右树R中，显然右树上的节点都大于所要查找的节点。

2.2 zig-zig旋转

 
    如上图所示，x节点的左子节点y，y的左子节点z，三者在一字型链上，且要查找的节点位于z节点为根的子树中。此时，对x节点和y节点进行zig，然后对z和y进行zig，使z成为中树的根，同时将y及其子树挂载到右树R上。

2.3 zig-zag旋转

 
    如上图所示，x节点的左子节点y，y的右子节点z，三者在之字型链上，且需要查找的元素位于以z为根的子树上。此时，先对x节点和y节点进行zig旋转，将x及其右子树挂载到右树R上，此时y成为中树的根节点；然后再对z节点和y节点进行zag旋转，使得z成为中树的根节点。

2.4 合并

 
    最后，找到节点或者遇到空节点之后，需要对左、中、右树进行合并。如图所示，将左树挂载到中树的最左下方（满足遍历顺序要求），将右树挂载到中树的最右下方（满足遍历顺序要求）。

 

父节点向左到左子节点-> zig

父节点向右到右子节点->zag

举例说明旋转操作

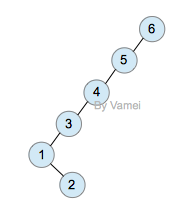
Original

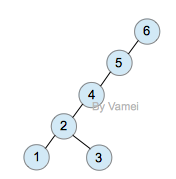
zig-zag (double rotation)

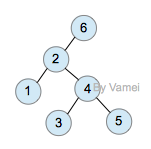
zig-zig

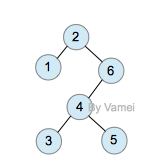
zig (single rotation at root)

伸展树的基本操作

    利用Splay操作，可以在伸展树上进行如下操作： 
(1) Find(x, S) 判断x是否在伸展树S表示的有序集中 
    首先按照普通的二叉查找树查找算法进行查找，如果找到元素x，则执行Splay(x, S)操作将x旋转到树根的位置。

(2) Insert(x, S) 将元素x插入到树中 
    首先按照普通的二叉查找树插入算法进行插入，然后执行Splay(x, S)

(3) Delete(x, S) 将元素x从伸展树S所表示的有序集中删除 
    首先按照普通的二叉查找树查找算法找到x的位置。如果x没有孩子或只有一个孩子，则直接将x删除，并通过Splay操作，将x节点的父节点调整到伸展树的根节点处。否则，向下查找x的后继节点y，用y替代x的位置，然后执行Splay(y, S)，将y调整为伸展树的根

(4) Join(S1, S2) 将两个伸展树S1, S2合并为一个伸展树。其中S1的所有元素小于S2中的所有元素。 
 
    首先按照普通的二叉查找树查找算法找到S1中最大元素x，然后执行Splay(x, S1)将x旋转到S1的根部，此时S1中的所有元素必然在x的左子树上，x的右子树为空，则可以将S2挂载到x的右子树位置。

(5) Split(x, S) 以x为界，将伸展树S分离为两棵伸展树S1和S2，其中S1中所有元素都小于x，S2中所有元素都大于x。 

    首先执行Find(x, S)，将元素x调整为伸展树的根节点，则x的左子树就是S1，右子树就是S2.

伸展树Splay(x,S)实现(c++)

1 自底向上的旋转方式

struct TreeNode{
    int data;
    TreeNode* left;
    TreeNode* right;
    TreeNode* parent;
    TreeNode(int d) :
        data(d), left(NULL), right(NULL), parent(NULL){};
};

TreeNode* gTreeRoot;
void Rotate(TreeNode* x, bool left_rotate){ //旋转x节点（将x节点 按照 left_rotate 指示 绕着其父节点y 进行左旋或者右旋
    TreeNode* y = x->parent;
    if (y == NULL){
        return;
    }

    if (left_rotate){
        y->right = x->left;
        if (!x->left){
            x->left->parent = y;
        }
    }
    else{
        y->left = x->right;
        if (!x->right){
            x->right->parent = y;
        }
    }

    x->parent = y->parent;
    if (!y->parent){
        if (y == y->parent->left){
            y->parent->left = x;
        }
        else{
            y->parent->right = x;
        }
    }

    if (y == gTreeRoot){ //全局的根节点
        gTreeRoot = x;
    }
}

//将节点x通过不断的Rotate操作，直到x成为f的子节点
void Splay(TreeNode* x, TreeNode* f){
    TreeNode* y = x->parent, *z = NULL;
    while (y != f){
        z = y->parent;
        if (z == f){
            Rotate(x, x == y->right);
        }
        else{
            if (!(x == y->left ^ y == z->left)){ //一字型 旋转 zig-zig
                Rotate(y, y == z->right);
                Rotate(x, x == y->right);
            }
            else{ //之字型旋转 zig-zag
                Rotate(x, x == y->right);

                //注意，上一步的rotate操作，x的地址没有发生改变，但是x地址指向的结构体中的各个域被修改为经过旋转之后的结构
                //所有，这里直接使用x即可
                Rotate(x, x == z->right);                 
            }
        }
    }
}

 2 自顶向下的方式旋转

struct TreeNode{
    int data;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int d = 0) :
        data(d), left(NULL), right(NULL){};
};

TreeNode* Splay(int i, TreeNode* t){
    TreeNode N, *l, *r, *y; // l, t, r 分别为左树、中树、右树
    if (t == NULL){
        return;
    }
    l = r = &N;            
    while (true){
        if (i < t->data){
            if (t->left == NULL){ //碰到空节点，结束
                break;
            }
            if (i < t->left->data){    //需要进行右旋
                y = t->left;
                t->left = y->right;
                y->right = t;
                t = y;
                if (t->left == NULL){
                    break;
                }
            }
            r->left = t;    //挂载到右树，最小的位置
            r = t;
            t = t->left; //将 z 升为中树的根节点
        }
        else if (i > t->data){
            if (t->right == NULL){
                break;
            }
            if (i > t->right->data){ //需要进行左旋
                y = t->right;
                t->right = y->left;
                y->left = t;
            }
            l->right = t;    //挂载到左树，最大的位置
            l = t;
            t = t->right;  //将z升为中树的根节点
        }
        else{
            break;
        }
    }
    l->right = t->left;  //将左、中、右树进行合并
    r->left = t->right;
    t->left = N.right;
    t->right = N.left;
    return t;
}