算法实践——舞蹈链(Dancing Links)算法求解数独
在“跳跃的舞者,舞蹈链(Dancing Links)算法——求解精确覆盖问题”一文中介绍了舞蹈链(Dancing Links)算法求解精确覆盖问题。
本文介绍该算法的实际运用,利用舞蹈链(Dancing Links)算法求解数独
在前文中可知,舞蹈链(Dancing Links)算法在求解精确覆盖问题时效率惊人。
那利用舞蹈链(Dancing Links)算法求解数独问题,实际上就是下面一个流程
1、把数独问题转换为精确覆盖问题
2、设计出数据矩阵
3、用舞蹈链(Dancing Links)算法求解该精确覆盖问题
4、把该精确覆盖问题的解转换为数独的解
首先看看数独问题(9*9的方格)的规则
1、每个格子只能填一个数字
2、每行每个数字只能填一遍
3、每列每个数字只能填一遍
4、每宫每个数字只能填一遍(宫的概念,参看“算法实践——数独的基本解法”)
那现在就是利用这个规则把数独问题转换为精确覆盖问题
可是,直观上面的规则,发现比较难以转换为精确覆盖问题。因此,把上面的表述换个说法
1、每个格子只能填一个数字
2、每行1-9的这9个数字都得填一遍(也就意味着每个数字只能填一遍)
3、每列1-9的这9个数字都得填一遍
4、每宫1-9的这9个数字都得填一遍
这样理解的话,数独问题转换为精确覆盖问题就相对简单多了。关键就是如何构造精确覆盖问题中的矩阵
我们把矩阵的每个列都定义成一个约束条件。
第1列定义成:(1,1)填了一个数字
第2列定义成:(1,2)填了一个数字
……
第9列定义成:(1,9)填了一个数字
第10列定义成:(2,1)填了一个数字
……
第18列定义成:(2,9)填了一个数字
……
第81列定义成:(9,9)填了一个数字
至此,用第1-81列完成了约束条件1:每个格子只能填一个数字
第N列(1≤N≤81)定义成:(X,Y)填了一个数字。
N、X、Y之间的关系是:X=INT((N-1)/9)+1;Y=((N-1) Mod 9)+1;N=(X-1)×9+Y
第82列定义成:在第1行填了数字1
第83列定义成:在第1行填了数字2
……
第90列定义成:在第1行填了数字9
第91列定义成:在第2行填了数字1
……
第99列定义成:在第2行填了数字9
……
第162列定义成:在第9行填了数字9
至此,用第82-162列(共81列)完成了约束条件2:每行1-9的这9个数字都得填一遍
第N列(82≤N≤162)定义成:在第X行填了数字Y。
N、X、Y之间的关系是:X=INT((N-81-1)/9)+1;Y=((N-81-1) Mod 9)+1;N=(X-1)×9+Y+81
第163列定义成:在第1列填了数字1
第164列定义成:在第1列填了数字2
……
第171列定义成:在第1列填了数字9
第172列定义成:在第2列填了数字1
……
第180列定义成:在第2列填了数字9
……
第243列定义成:在第9列填了数字9
至此,用第163-243列(共81列)完成了约束条件3:每列1-9的这9个数字都得填一遍
第N列(163≤N≤243)定义成:在第X列填了数字Y。
N、X、Y之间的关系是:X=INT((N-162-1)/9)+1;Y=((N-162-1) Mod 9)+1;N=(X-1)×9+Y+162
第244列定义成:在第1宫填了数字1
第245列定义成:在第1宫填了数字2
……
第252列定义成:在第1宫填了数字9
第253列定义成:在第2宫填了数字1
……
第261列定义成:在第2宫填了数字9
……
第324列定义成:在第9宫填了数字9
至此,用第244-324列(共81列)完成了约束条件4:每宫1-9的这9个数字都得填一遍
第N列(244≤N≤324)定义成:在第X宫填了数字Y。
N、X、Y之间的关系是:X=INT((N-243-1)/9)+1;Y=((N-243-1) Mod 9)+1;N=(X-1)×9+Y+243
至此,用了324列完成了数独的四个约束条件,矩阵的列定义完成
那接下来,就是把数独转换为矩阵
数独问题中,每个格子分两种情况。有数字的格子、没数字的格子。
有数字的格子
以例子来说明,在(4,2)中填的是7
把(4,2)中填的是7,解释成4个约束条件
1、在(4,2)中填了一个数字。
2、在第4行填了数字7
3、在第2列填了数字7
4、在第4宫填了数字7(坐标(X,Y)到宫N的公式为:N=INT((X-1)/3)×3+INT((Y-1)/3)+1)
那么这4个条件,分别转换成矩阵对应的列为
1、在(4,2)中填了一个数字。对应的列N=(4-1)×9+2=29
2、在第4行填了数字7。对应的列N=(4-1)×9+7+81=115
3、在第2列填了数字7。对应的列N=(2-1)×9+7+162=178
4、在第4宫填了数字7。对应的列N=(4-1)×9+7+243=277
于是,(4,2)中填的是7,转成矩阵的一行就是,第29、115、178、277列是1,其余列是0。把这1行插入到矩阵中去。
没数字的格子
还是举例说明,在(5,8)中没有数字
把(5,8)中没有数字转换成
(5,8)中填的是1,转成矩阵的一行就是,第44、118、226、289列是1,其余列是0。
(5,8)中填的是2,转成矩阵的一行就是,第44、119、227、290列是1,其余列是0。
(5,8)中填的是3,转成矩阵的一行就是,第44、120、228、291列是1,其余列是0。
(5,8)中填的是4,转成矩阵的一行就是,第44、121、229、292列是1,其余列是0。
(5,8)中填的是5,转成矩阵的一行就是,第44、122、230、293列是1,其余列是0。
(5,8)中填的是6,转成矩阵的一行就是,第44、123、231、294列是1,其余列是0。
(5,8)中填的是7,转成矩阵的一行就是,第44、124、232、295列是1,其余列是0。
(5,8)中填的是8,转成矩阵的一行就是,第44、125、233、296列是1,其余列是0。
(5,8)中填的是9,转成矩阵的一行就是,第44、126、234、297列是1,其余列是0。
把这9行插入到矩阵中。由于这9行的第44列都是1(不会有其他行的44列会是1),也就是说这9行中必只有1行(有且只有1行)选中(精确覆盖问题的定义,每列只能有1个1),是最后解的一部分。这就保证了最后解在(5,8)中只有1个数字。
这样,从数独的格子依次转换成行(1行或者9行)插入到矩阵中。完成了数独问题到精确覆盖问题的转换。
接下来求解精确覆盖问题就交给舞蹈链(Dancing Links)算法,详情参看“跳跃的舞者,舞蹈链(Dancing Links)算法——求解精确覆盖问题”
Public Interface I_Sudoku
Function SetLine(ByVal Row As Integer, ByVal ParamArray Value() As Integer) As Boolean
Function Calculate() As String
Sub Init()
End Interface
Public Class clsSudokuDLX
Implements I_Sudoku
Private _Dance As clsDancingLinks
Private _Num(80) As Integer
Public Sub New()
Init()
End Sub
Public Function SetLine(Row As Integer, ParamArray Value() As Integer) As Boolean Implements I_Sudoku.SetLine
Dim I As Integer
For I = 0 To IIf(Value.Length < 10, Value.Length - 1, 8)
_Num(Row * 9 - 9 + I) = Value(I)
Next
Return True
End Function
Public Function Calculate() As String Implements I_Sudoku.Calculate
Dim I As Integer, J As Integer
Dim X As Integer, Y As Integer
Dim Index As New List(Of Integer), Value As New List(Of Integer)
Dim C1 As Integer, C2 As Integer, C3 As Integer, C4 As Integer
For I = 0 To 80
X = Int(I / 9)
Y = I Mod 9
If _Num(I) > 0 Then
C1 = X * 9 + Y + 1
C2 = X * 9 + _Num(I) + 81
C3 = Y * 9 + _Num(I) + 162
C4 = (Int(X / 3) * 3 + Int(Y / 3)) * 9 + _Num(I) + 243
_Dance.AppendLineByIndex(C1, C2, C3, C4)
Index.Add(I)
Value.Add(_Num(I))
Else
C1 = X * 9 + Y + 1
C2 = X * 9 + 1 + 81
C3 = Y * 9 + 1 + 162
C4 = (Int(X / 3) * 3 + Int(Y / 3)) * 9 + 1 + 243
_Dance.AppendLineByIndex(C1, C2, C3, C4)
Index.Add(I)
Value.Add(1)
For J = 2 To 9
_Dance.AppendLineByIndex(C1, C2 + J - 1, C3 + J - 1, C4 + J - 1)
Index.Add(I)
Value.Add(J)
Next
End If
Next
Dim P() As Integer = _Dance.Dance
For I = 0 To 80
_Num(Index.Item(P(I) - 1)) = Value.Item(P(I) - 1)
Next
Dim V As String = ""
For I = 0 To 80
V = V & _Num(I) & " "
If I Mod 9 = 8 Then V &= vbNewLine
Next
Return V
End Function
Public Sub Init() Implements I_Sudoku.Init
_Dance = New clsDancingLinks(324)
Dim I As Integer
For I = 0 To 80
_Num(I) = 0
Next
End Sub
End Class
上面的代码给出了clsSudokuDLX的代码,通过调用clsDancingLinks类来求解数独。I_Sudoku接口没什么特殊意义,仅仅是为了测试方便而已。clsDancingLinks类的代码这里就不贴了,在“跳跃的舞者,舞蹈链(Dancing Links)算法——求解精确覆盖问题”里有
对三个数独问题求解来对比算法的效率
先看看三个数独
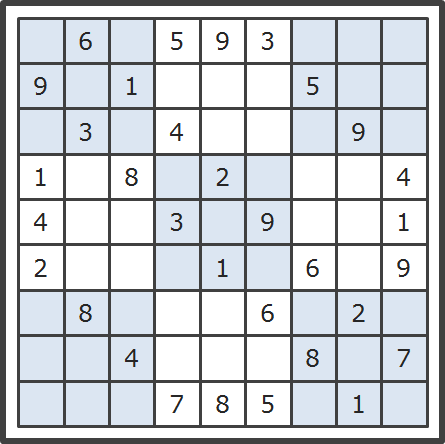
数独一:简单的数独
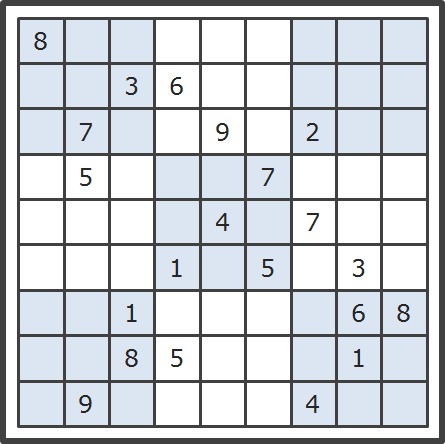
数独二:有点难度的数独
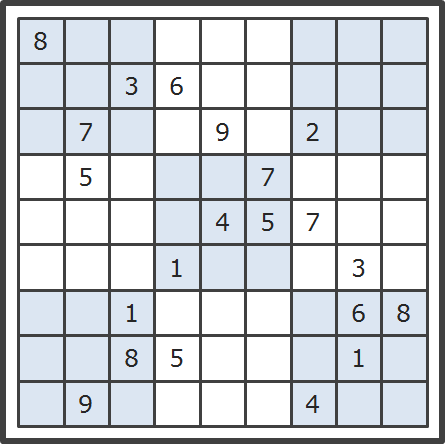
数独三:高难度的数独。虽然和数独二比较仅仅差了一个数字的位置,但是求解的难度提高了不止一个等级。
时间效率的对比
我们分别对三个数独进行百次的求解,剔除明显异于平均的时间,再取平均值
暴力破解法
数独一:0.114毫秒
数独二:0.238毫秒
数独三:15.706毫秒
舞蹈链(Dancing Links)算法
数独一:876.161毫秒(这个差距有点大,近乎7700倍,和我的期望值差距比较大)
数独二:775839.5毫秒=775秒840毫秒≈12.93分钟(我只做了三次测试,第一次等了5分钟,没结果,就退出了;第二次777348毫秒;第三次774331毫秒)
数独三:只做了一次测试,时间约40分钟,还没结果,就退出了
从上面的测试结果来看,舞蹈链(Dancing Links)算法从时间效率的角度来看,是完败于暴力破解法的
空间效率的对比
暴力破解法
数独一:在求解的过程中,一路唯一数单元格到底,没有缓存数据。故空间占用81字节。
数独二:在求解的过程中,最多向栈Q缓存了12步的数据。故占用空间81+12*81=972字节
数独三:在求解的过程中,最多向栈Q缓存了21步的数据。故占用空间81+21*81=1782字节
舞蹈链(Dancing Links)算法
数独一:题目提供了32个数字,则矩阵一共有32*1+(81-32)*9=473行,每行4个节点,则一共有473*4+324+1=2217个节点。每个节点6个分量,则一共要13302个字节。另程序在每行额外提供2个字节缓存相关信息。故一共要11844+473*2=14248字节
数独二:题目提供了21个数字,则矩阵一共有21*1+(81-21)*9=561行,每行4个节点,则一共有561*4+324+1=2569个节点。每个节点6个分量,则一共要15414个字节。另程序在每行额外提供2个字节缓存相关信息。故一共要15414+561*2=16536字节
数独三:题目提供了21个数字,则矩阵一共有21*1+(81-21)*9=561行,每行4个节点,则一共有561*4+324+1=2569个节点。每个节点6个分量,则一共要15414个字节。另程序在每行额外提供2个字节缓存相关信息。故一共要15414+561*2=16536字节
以上的分析,舞蹈链(Dancing Links)算法从空间效率的角度来看,是完败于暴力破解法的
做分析做到这,结果出乎我的意料。虽然我估计舞蹈链(Dancing Links)算法不见得优于暴力破解法,但没想到差距会那么大。不过,也可以理解,舞蹈链(Dancing Links)算法仅仅是利用了十字双向循环链的数据结构解决了缓存和回溯的难题,但本质上还是回溯法,还是暴力破解法。
针对该数独问题进行优化舞蹈链(Dancing Links)算法
回顾前文“跳跃的舞者,舞蹈链(Dancing Links)算法——求解精确覆盖问题”,可以发现,在Dance(K)函数调用的时候,是直接调用_Head.Right来获得未求解列。由于精确覆盖问题是要求每个列都要覆盖到,因此,在算法中调用未求解列的先后顺序那就不是最重要了。假如,现在有两个未求解列C1和C2,C1列有8个元素,C2列有4个元素。最坏的情况,从C1列求解,需要调用8次Dance(K+1),而从C2列求解,需要调用4次Dance(K+1)。感觉上从C2列求解比从C1列求解效率要高些。因此,在Dance(K)函数调用的时候,先找寻列元素最少的未求解列,再依次求解,可能效率会高点。我们把这个称之为改进的舞蹈链(Improve Dancing Links)算法
给每个列首元素(除却Head元素)添加一个Count分量,表示这个列首所在列的其他元素的个数。
因此,在原算法的基础上,把C1=Head.Right改成获得Count分量最少的列首元素。代码贴于下方,修改的部分用红色标示
Public Class clsDancingLinksImprove
Private Left() As Integer, Right() As Integer, Up() As Integer, Down() As Integer
Private Row() As Integer, Col() As Integer
Private _Head As Integer
Private _Rows As Integer, _Cols As Integer, _NodeCount As Integer
Private Count() As Integer
Private Ans() As Integer
Public Sub New(ByVal Cols As Integer)
ReDim Left(Cols), Right(Cols), Up(Cols), Down(Cols), Row(Cols), Col(Cols), Ans(Cols)
ReDim Count(Cols)
Dim I As Integer
Up(0) = 0
Down(0) = 0
Right(0) = 1
Left(0) = Cols
For I = 1 To Cols
Up(I) = I
Down(I) = I
Left(I) = I - 1
Right(I) = I + 1
Col(I) = I
Row(I) = 0
Count(I) = 0
Next
Right(Cols) = 0
_Rows = 0
_Cols = Cols
_NodeCount = Cols
_Head = 0
End Sub
Public Sub AppendLine(ByVal ParamArray Value() As Integer)
_Rows += 1
If Value.Length = 0 Then Exit Sub
Dim I As Integer, K As Integer = 0
For I = 0 To Value.Length - 1
If Value(I) = 1 Then
_NodeCount += 1
ReDim Preserve Left(_NodeCount)
ReDim Preserve Right(_NodeCount)
ReDim Preserve Up(_NodeCount)
ReDim Preserve Down(_NodeCount)
ReDim Preserve Row(_NodeCount)
ReDim Preserve Col(_NodeCount)
ReDim Preserve Ans(_NodeCount)
If K = 0 Then
Left(_NodeCount) = _NodeCount
Right(_NodeCount) = _NodeCount
K = 1
Else
Left(_NodeCount) = _NodeCount - 1
Right(_NodeCount) = Right(_NodeCount - 1)
Left(Right(_NodeCount - 1)) = _NodeCount
Right(_NodeCount - 1) = _NodeCount
End If
Down(_NodeCount) = I + 1
Up(_NodeCount) = Up(I + 1)
Down(Up(I + 1)) = _NodeCount
Up(I + 1) = _NodeCount
Row(_NodeCount) = _Rows
Col(_NodeCount) = I + 1
Count(I + 1) += 1
End If
Next
End Sub
Public Sub AppendLineByIndex(ByVal ParamArray Index() As Integer)
_Rows += 1
If Index.Length = 0 Then Exit Sub
Dim I As Integer, K As Integer = 0
ReDim Preserve Left(_NodeCount + Index.Length)
ReDim Preserve Right(_NodeCount + Index.Length)
ReDim Preserve Up(_NodeCount + Index.Length)
ReDim Preserve Down(_NodeCount + Index.Length)
ReDim Preserve Row(_NodeCount + Index.Length)
ReDim Preserve Col(_NodeCount + Index.Length)
ReDim Preserve Ans(_NodeCount + Index.Length)
For I = 0 To Index.Length - 1
_NodeCount += 1
If I = 0 Then
Left(_NodeCount) = _NodeCount
Right(_NodeCount) = _NodeCount
Else
Left(_NodeCount) = _NodeCount - 1
Right(_NodeCount) = Right(_NodeCount - 1)
Left(Right(_NodeCount - 1)) = _NodeCount
Right(_NodeCount - 1) = _NodeCount
End If
Down(_NodeCount) = Index(I)
Up(_NodeCount) = Up(Index(I))
Down(Up(Index(I))) = _NodeCount
Up(Index(I)) = _NodeCount
Row(_NodeCount) = _Rows
Col(_NodeCount) = Index(I)
Count(Index(I)) += 1
Next
End Sub
Public Function Dance() As Integer()
Return IIf(Dance(0) = True, Ans, Nothing)
End Function
Private Function Dance(ByVal K As Integer) As Boolean
If (Right(_Head) = _Head) Then
ReDim Preserve Ans(K - 1)
Return True
End If
Dim P As Integer, C1 As Integer
P = Right(_Head)
C1 = P
Do While P <> _Head
If Count(P) < Count(C1) Then C1 = P
P = Right(P)
Loop
If Count(C1) < 1 Then Return False
RemoveCol(C1)
Dim I As Integer, J As Integer
I = Down(C1)
Do While I <> C1
Ans(K) = Row(I)
J = Right(I)
Do While J <> I
RemoveCol(Col(J))
J = Right(J)
Loop
If Dance(K + 1) Then Return True
J = Left(I)
Do While J <> I
ResumeCol(Col(J))
J = Left(J)
Loop
I = Down(I)
Loop
ResumeCol(C1)
Return False
End Function
Public Sub RemoveCol(ByVal ColIndex As Integer)
Left(Right(ColIndex)) = Left(ColIndex)
Right(Left(ColIndex)) = Right(ColIndex)
Dim I As Integer, J As Integer
I = Down(ColIndex)
Do While I <> ColIndex
J = Right(I)
Do While J <> I
Up(Down(J)) = Up(J)
Down(Up(J)) = Down(J)
Count(Col(J)) -= 1
J = Right(J)
Loop
I = Down(I)
Loop
End Sub
Public Sub ResumeCol(ByVal ColIndex As Integer)
Left(Right(ColIndex)) = ColIndex
Right(Left(ColIndex)) = ColIndex
Dim I As Integer, J As Integer
I = Up(ColIndex)
Do While (I <> ColIndex)
J = Right(I)
Do While J <> I
Up(Down(J)) = J
Down(Up(J)) = J
Count(Col(J)) += 1
J = Right(J)
Loop
I = Up(I)
Loop
End Sub
End Class
这样修改后还有一个好处是,如果Count分量最少的列首元素的Count分量是0的话,那么说明当前无解(说明没有行能覆盖该列首元素所在的列),直接返回False,省掉调用Dance(K+1)的步骤。
看看改进的舞蹈链(Improve Dancing Links)算法的效率
时间效率
数独一:6.31毫秒
数独二:8.50毫秒
数独三:11.34毫秒
空间效率
数独一:题目提供了32个数字,则矩阵一共有32*1+(81-32)*9=473行,每行4个节点,则一共有473*4+324+1=2217个节点。每个节点6个分量,则一共要13302个字节。另程序在每行额外提供2个字节缓存相关信息,每个列要增加Count分量。故一共要13302+473*2+325=14573字节
数独二:题目提供了21个数字,则矩阵一共有21*1+(81-21)*9=561行,每行4个节点,则一共有561*4+324+1=2569个节点。每个节点6个分量,则一共要15414个字节。另程序在每行额外提供2个字节缓存相关信息。每个列要增加Count分量。故一共要15414+561*2+325=16861字节
数独三:题目提供了21个数字,则矩阵一共有21*1+(81-21)*9=561行,每行4个节点,则一共有561*4+324+1=2569个节点。每个节点6个分量,则一共要15414个字节。另程序在每行额外提供2个字节缓存相关信息。每个列要增加Count分量。故一共要15414+561*2+325=16861字节
以上的分析,改进的舞蹈链(Improve Dancing Lonks)算法在空间效率上还是完败。但是时间效率上从看,在低难度的数独问题上,虽然和暴力破解法还是有差距,但是差距比没有优化前要小了很多;在高难度的数度问题上,时间效率比暴力破解法要高。
舞蹈链(Dancing Links)算法针对数独问题还能再优化。我们来看看第二个优化的方向
在求解精确覆盖问题中,返回的答案实际上是行的集合,集合的一个特性是无序性。也就意味着,如果答案是唯一的话,改变行在矩阵中的顺序,不影响最后答案的输出,无论这行换到什么位置,最后的答案始终包含着这行(如果答案不是唯一的,也没啥太大的影响)。也就是说,行的顺序不影响最终答案的求解。
我们就从这个方向入手
在构造矩阵的时候,先遍历数独的格子,先把有数字的格子转换为行,插入到矩阵中。很显然,这些行一定会被选中(想想看么,原问题中(4,2)填的是7,如果该行没选中,结果出现了(4,2)填的是9,那不是一件很搞笑的事么)。
由于是精确覆盖问题,每列只能有1个1,而上面的插入的几行一定会被选中。那么,在接下来插入的行如果和上面的行相冲的话(两个行有相同的列有1),那么,后插入的行是个无效的行(肯定不会被选中)。这些无效的行插入到矩阵中,虽然不会影响最终的结果,但是肯定影响求解的效率(空间和时间都有所损耗),而这样的无效行其实有不少。
我们要采用特殊的手法,来避免这些无效的行插入到矩阵中。分两步走
1、先遍历数独的格子,把那些有数字的格子转换为行,插入到矩阵中。在插入的同时,把包含1的列的列首元素的Count分量设置为-1(起到后面判别的作用)。
由于这些行一定能被选中,是答案的一部分,那么把这些行的行号置入到答案列表中,并把这些列的列首元素从水平双向链中移除(手动移除比调用RemoveCol方法快)
2、在遍历没有数字的格子,转换为若干行(1个格子9行)插入到矩阵中。在插入到矩阵的时候,判断包含1的列的列首元素的Count分量。如果是-1,说明新插入的行和第1步中的某些行相冲,是个无效行,没有必要插入到矩阵中;如果不是-1,说明是个有效行,插入到矩阵中。
经过这个优化,能大大减少矩阵的规模(列不变,行减少了不少),我们称之为数独的舞蹈链(Sudoku Dancing Links)算法。
Public Class clsSudokuDLXBySudoku
Implements I_Sudoku
Private _Dance As clsDancingLinksSudoku
Private _Num(80) As Integer
Public Sub New()
Init()
End Sub
Public Function SetLine(Row As Integer, ParamArray Value() As Integer) As Boolean Implements I_Sudoku.SetLine
Dim I As Integer
For I = 0 To IIf(Value.Length < 10, Value.Length - 1, 8)
_Num(Row * 9 - 9 + I) = Value(I)
Next
Return True
End Function
Public Function Calculate() As String Implements I_Sudoku.Calculate
Dim I As Integer, J As Integer
Dim X As Integer, Y As Integer
Dim Index As New List(Of Integer), Value As New List(Of Integer)
Dim C1 As Integer, C2 As Integer, C3 As Integer, C4 As Integer
For I = 0 To 80
X = Int(I / 9)
Y = I Mod 9
If _Num(I) > 0 Then
C1 = X * 9 + Y + 1
C2 = X * 9 + _Num(I) + 81
C3 = Y * 9 + _Num(I) + 162
C4 = (Int(X / 3) * 3 + Int(Y / 3)) * 9 + _Num(I) + 243
_Dance.AppendLineByIndex(C1, C2, C3, C4)
Index.Add(I)
Value.Add(_Num(I))
End If
Next
_Dance.CompleteInsertMustSelectRow()
For I = 0 To 80
X = Int(I / 9)
Y = I Mod 9
If _Num(I) = 0 Then
C1 = X * 9 + Y + 1
C2 = X * 9 + 1 + 81
C3 = Y * 9 + 1 + 162
C4 = (Int(X / 3) * 3 + Int(Y / 3)) * 9 + 1 + 243
If _Dance.AppendLineByIndex(C1, C2, C3, C4) = True Then
Index.Add(I)
Value.Add(1)
End If
For J = 2 To 9
If _Dance.AppendLineByIndex(C1, C2 + J - 1, C3 + J - 1, C4 + J - 1) = True Then
Index.Add(I)
Value.Add(J)
End If
Next
End If
Next
Dim P() As Integer = _Dance.Dance
For I = 0 To 80
_Num(Index.Item(P(I) - 1)) = Value.Item(P(I) - 1)
Next
Dim V As String = ""
For I = 0 To 80
V = V & _Num(I) & " "
If I Mod 9 = 8 Then V &= vbNewLine
Next
Return V
End Function
Public Sub Init() Implements I_Sudoku.Init
_Dance = New clsDancingLinksSudoku(324)
Dim I As Integer
For I = 0 To 80
_Num(I) = 0
Next
End Sub
End Class
Public Class clsDancingLinksSudoku
Private Left() As Integer, Right() As Integer, Up() As Integer, Down() As Integer
Private Row() As Integer, Col() As Integer
Private _Head As Integer
Private _Rows As Integer, _Cols As Integer, _NodeCount As Integer
Private Count() As Integer
Private Ans() As Integer
Private _HadInsertMustSelectRow As Integer
Public Sub New(ByVal Cols As Integer)
ReDim Left(Cols), Right(Cols), Up(Cols), Down(Cols), Row(Cols), Col(Cols), Ans(Cols)
ReDim Count(Cols)
Dim I As Integer
Up(0) = 0
Down(0) = 0
Right(0) = 1
Left(0) = Cols
For I = 1 To Cols
Up(I) = I
Down(I) = I
Left(I) = I - 1
Right(I) = I + 1
Col(I) = I
Row(I) = 0
Count(I) = 0
Next
Right(Cols) = 0
_Rows = 0
_Cols = Cols
_NodeCount = Cols
_Head = 0
_HadInsertMustSelectRow = 0
End Sub
Public Function AppendLine(ByVal ParamArray Value() As Integer) As Boolean
Dim V As New List(Of Integer)
Dim I As Integer
For I = 0 To Value.Length - 1
If Value(I) = 1 Then V.Add(I + 1)
Next
Return AppendLineByIndex(V.ToArray)
End Function
Public Function AppendLineByIndex(ByVal ParamArray Index() As Integer) As Boolean
Dim I As Integer, K As Integer = 0
If _HadInsertMustSelectRow > 0 Then
If Index.Length = 0 Then
_Rows += 1
Return True
Else
For I = 0 To Index.Length - 1
If Count(Index(I)) = -1 Then Return False
Next
End If
Else
If Index.Length = 0 Then Return False
End If
_Rows += 1
ReDim Preserve Left(_NodeCount + Index.Length)
ReDim Preserve Right(_NodeCount + Index.Length)
ReDim Preserve Up(_NodeCount + Index.Length)
ReDim Preserve Down(_NodeCount + Index.Length)
ReDim Preserve Row(_NodeCount + Index.Length)
ReDim Preserve Col(_NodeCount + Index.Length)
ReDim Preserve Ans(_NodeCount + Index.Length)
For I = 0 To Index.Length - 1
_NodeCount += 1
If I = 0 Then
Left(_NodeCount) = _NodeCount
Right(_NodeCount) = _NodeCount
Else
Left(_NodeCount) = _NodeCount - 1
Right(_NodeCount) = Right(_NodeCount - 1)
Left(Right(_NodeCount - 1)) = _NodeCount
Right(_NodeCount - 1) = _NodeCount
End If
Down(_NodeCount) = Index(I)
Up(_NodeCount) = Up(Index(I))
Down(Up(Index(I))) = _NodeCount
Up(Index(I)) = _NodeCount
Row(_NodeCount) = _Rows
Col(_NodeCount) = Index(I)
If _HadInsertMustSelectRow > 0 Then
Count(Index(I)) += 1
Else
Count(Index(I)) = -1
End If
Next
Return True
End Function
Public Sub CompleteInsertMustSelectRow()
Dim I As Integer
For I = 1 To _Cols
If Count(I) = -1 Then
Left(Right(I)) = Left(I)
Right(Left(I)) = Right(I)
End If
Next
For I = 1 To _Rows
Ans(I - 1) = I
Next
_HadInsertMustSelectRow = _Rows
End Sub
Public Function Dance() As Integer()
Return IIf(Dance(_HadInsertMustSelectRow) = True, Ans, Nothing)
End Function
Private Function Dance(ByVal K As Integer) As Boolean
If (Right(_Head) = _Head) Then
ReDim Preserve Ans(K - 1)
Return True
End If
Dim P As Integer, C1 As Integer
P = Right(_Head)
C1 = P
Do While P <> _Head
If Count(P) < Count(C1) Then C1 = P
P = Right(P)
Loop
If Count(C1) < 1 Then Return False
RemoveCol(C1)
Dim I As Integer, J As Integer
I = Down(C1)
Do While I <> C1
Ans(K) = Row(I)
J = Right(I)
Do While J <> I
RemoveCol(Col(J))
J = Right(J)
Loop
If Dance(K + 1) Then Return True
J = Left(I)
Do While J <> I
ResumeCol(Col(J))
J = Left(J)
Loop
I = Down(I)
Loop
ResumeCol(C1)
Return False
End Function
Public Sub RemoveCol(ByVal ColIndex As Integer)
Left(Right(ColIndex)) = Left(ColIndex)
Right(Left(ColIndex)) = Right(ColIndex)
Dim I As Integer, J As Integer
I = Down(ColIndex)
Do While I <> ColIndex
J = Right(I)
Do While J <> I
Up(Down(J)) = Up(J)
Down(Up(J)) = Down(J)
Count(Col(J)) -= 1
J = Right(J)
Loop
I = Down(I)
Loop
End Sub
Public Sub ResumeCol(ByVal ColIndex As Integer)
Left(Right(ColIndex)) = ColIndex
Right(Left(ColIndex)) = ColIndex
Dim I As Integer, J As Integer
I = Up(ColIndex)
Do While (I <> ColIndex)
J = Right(I)
Do While J <> I
Up(Down(J)) = J
Down(Up(J)) = J
Count(Col(J)) += 1
J = Right(J)
Loop
I = Up(I)
Loop
End Sub
End Class
通过_HadInsertMustSelectRow来决定插入行的数据。如果_HadInsertMustSelectRow=0说明当前插入行为必选行,设置Count(J)的值为-1。如果_HadInsertMustSelectRow>0说明当前行为可选行,判断和之前的必选行是否有冲突,如果有,说明本行必不可选,不比再插入到矩阵里了。通过CompleteInsertMustSelectRow方法来修改_HadInsertMustSelectRow参数,来决定行的性质
数独的舞蹈链(Sudoku Dancing Links)算法的效率
时间效率
数独一:1.31毫秒
数独二:2.81毫秒
数独三:5.56毫秒
空间效率
数独一:矩阵一共有164行,每行4个节点,则一共有164*4+324+1=981个节点。每个节点6个分量,则一共要5886个字节。另程序在每行额外提供2个字节缓存相关信息,每个列要增加Count分量。故一共要5886+164*2+325=6539字节
数独二:矩阵一共有276行,每行4个节点,则一共有276*4+324+1=1429个节点。每个节点6个分量,则一共要8574个字节。另程序在每行额外提供2个字节缓存相关信息。每个列要增加Count分量。故一共要8574+276*2+325=9451字节
数独三:矩阵一共有275行,每行4个节点,则一共有275*4+324+1=1425个节点。每个节点6个分量,则一共要8550个字节。另程序在每行额外提供2个字节缓存相关信息。每个列要增加Count分量。故一共要8550+275*2+325=9425字节
可以看出,数独的舞蹈链(Sudoku Dancing Links)算法比改进的舞蹈链算法(Improve Dancing Links)算法,无论是时间效率上还是空间效率上都有了很大的改进。但是和暴力破解法相比,在简单的数独问题上,时间和空间都不占优势,在高难度的数独问题上,数独的舞蹈链算法还是在时间上占有一点优势的。这还是说明了一点,舞蹈链(Dancing Links)算法本质上也是暴力破解法,只是利用巧妙的数据结构实现了高效的缓存和回溯。
以上是我对用舞蹈链(Dancing Links)算法求解数独问题的分析,经过两次优化后,数独的舞蹈链(Sudoku Dancing Links)算法已经达到比较好的效果。但能不能再优化呢?能优化到全面超越暴力破解法?目前我没有看出其他的优化方向,如有,望网友不吝赐教,大家共同进步。
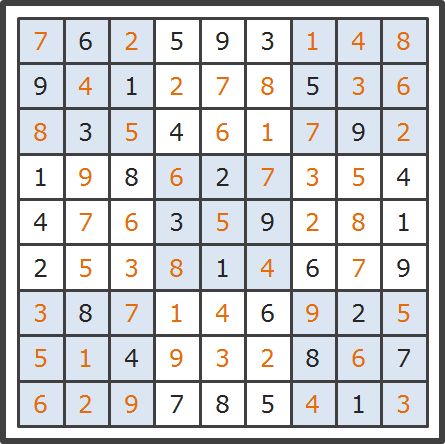
最后,给出三个数独的解
数独一:
数独二:
数独三: