【笔记】计算几何模板
引言
参考刘汝佳大白书,有一些自己的修改的相关代码
模板题AC 代码
UVa11178 Morley定理 点与直线计算
LA 3263 好看的一笔画 欧拉定理、点与直线计算
UVa11796 Dog Distance 点与直线计算、相对运动
LA2572 Viva Confetti 圆的计算
UVA10652 凸包
LA4728 Square 凸包、旋转卡壳
LA4973 Ardenia 三维线段距离
LA4589 Asteroids均匀密度凸多边形重心
模板
Part 0 基本部分
计算几何零散知识
精度
const double eps = 1e-9;
- 圆周率
const double PI = acos(-1);
- 比较函数
int dcmp(double x){return fabs(x)<eps?0:(x<0?-1:1);}
-
三角形外接圆、内切圆、旁切圆、九点圆
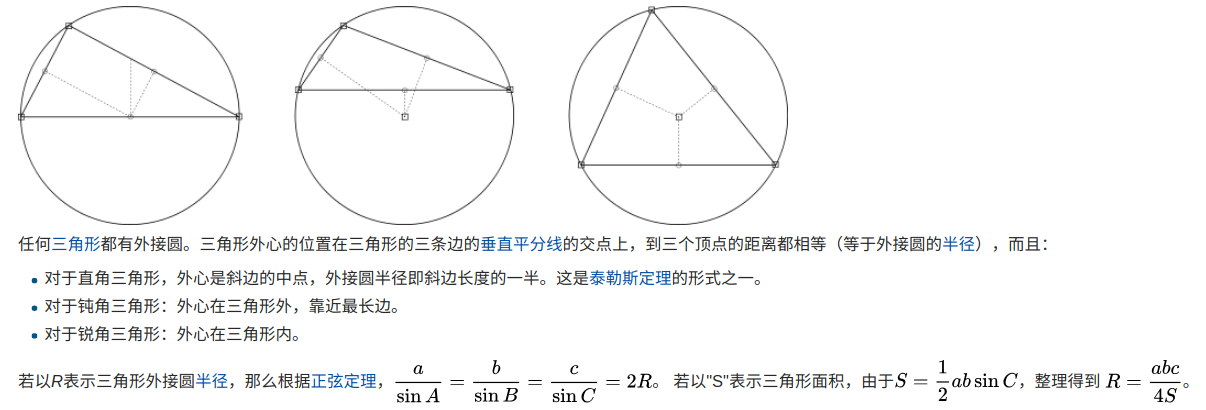
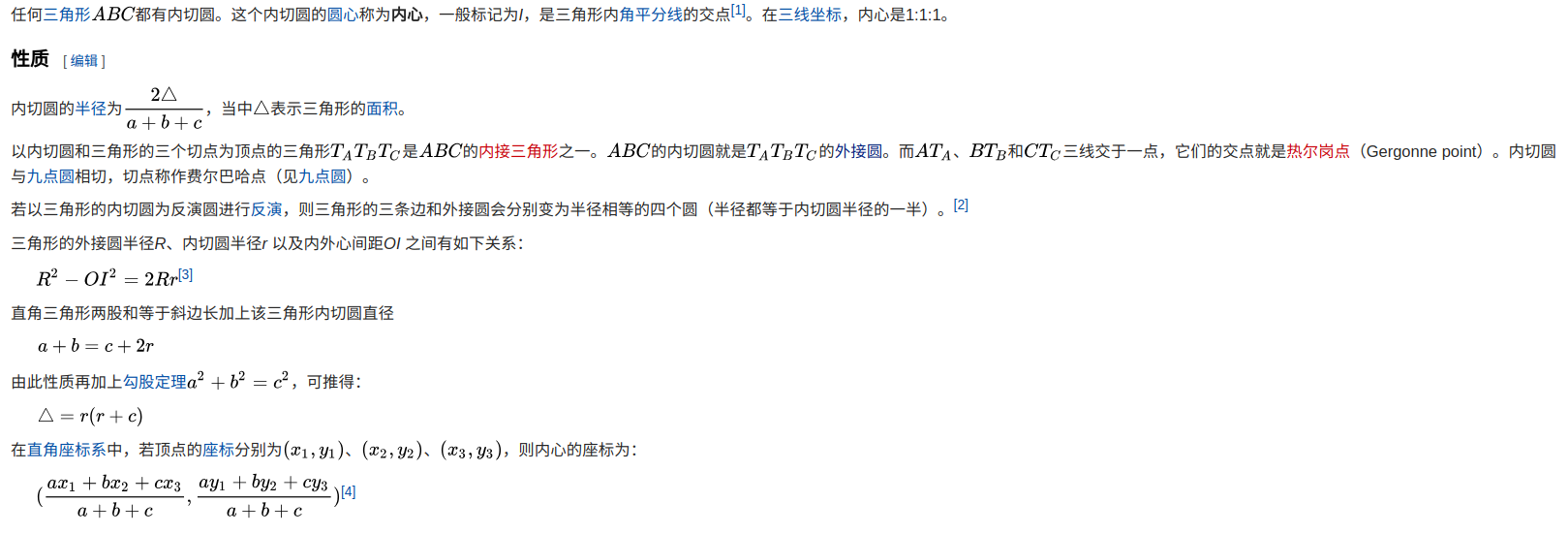


-
PICK定理

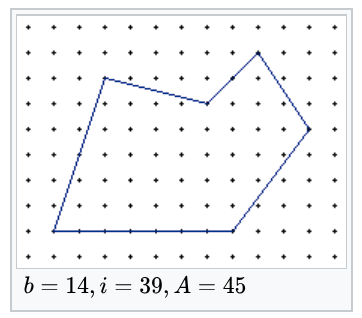

求三角形内部格点数
int Cross(Point A,Point B){ return abs(A.x*B.y-A.y*B.x);}
int cal_on(Point A){return abs(__gcd(A.x,A.y));}
int main(){
while(a[0].input()){
a[1].input();a[2].input();
if(a[0]==Point(0,0)&&a[1]==Point(0,0)&&a[2]==Point(0,0))return 0;
int A = Cross(a[1]-a[0],a[2]-a[0]);
int b = cal_on(a[0]-a[1])+cal_on(a[0]-a[2])+cal_on(a[1]-a[2]);
printf("%d\n",(A-b+2)/2);
}
}
- 分数类
struct Rat {
ll fz, fm;
Rat(ll _fz=0):fz(_fz),fm(1){}
Rat(ll _fz,ll _fm):fz(_fz),fm(_fm){ll _=abs(__gcd(fz,fm));fz/=_;fm/=_;}
Rat operator +(const Rat &o)const{
ll x = fm/__gcd(fm,o.fm)*o.fm;
return Rat(fz*(x/fm)+o.fz*(x/o.fm),x);
}
friend Rat operator -(const Rat &now,const Rat &o){
Rat oo = o;
oo.fz=-oo.fz;
return now+oo;
}
Rat operator *(const Rat &o)const{
return Rat(fz*o.fz,fm*o.fm);
}
friend bool operator <(const Rat &now,const Rat &o){
Rat res=now-o; return res.fz<0;
}
friend bool operator >(const Rat&now,const Rat &o){
Rat res=now-o; return res.fz>0;
}
bool operator ==(const Rat &o)const{
return fz==o.fz&&fm==o.fm;
}
};
Simpson自适应积分
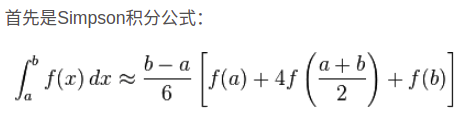
1.取三个点a, (a+b)/2, b
2.利用Simpson积分公式分别计算原图像在[a, b], [a, (a+b)/2], [(a+b)/2. b]的面积(分别记为S0, S1, S1),若S0与S1+S2的值相差无几,则可以认为S0为原图像在[a, b]内的面积。直接返回这个面积,否则继续划分下去
应用:求圆的面积并
#include<bits/stdc++.h>
using namespace std;
const double eps=1e-13;
int dcmp(double x){return fabs(x)<=eps?0:(x<0?-1:1);}
struct Point{
double x,y;
Point(double _x=0,double _y=0):x(_x),y(_y){}
bool operator <(const Point& o)const{return dcmp(x-o.x)<0||(dcmp(x-o.x)==0&&dcmp(y-o.y)<0);}
bool operator == (const Point& o)const{return dcmp(x-o.x)==0&&dcmp(y-o.y)==0;}
Point operator + (const Point& o)const{return Point(x+o.x,y+o.y);}
Point operator - (const Point& o)const{return Point(x-o.x,y-o.y);}
Point operator * (double o)const{return Point(x*o,y*o);}
Point operator / (double o)const{return Point(x/o,y/o);}
int input(){return scanf("%lf%lf",&x,&y);}
};
struct Circle{
Point p;double r;
bool operator <(const Circle &o)const{
return r<o.r;
}
void input(){
p.input();scanf("%lf",&r);
}
}c[1005];
int n;
double Min=1001,Max=-1001;
bool flag[1005];
pair<double,double>a[1005];
double ans;
double length(Point a){
return sqrt(a.x*a.x+a.y*a.y);
}
double F(double x){
int cnt=0;
for(int i=1;i<=n;i++){
double dis=fabs(c[i].p.x-x);
if(dcmp(dis-c[i].r)<0){
double len=sqrt(c[i].r*c[i].r-dis*dis);
a[++cnt]=make_pair(c[i].p.y-len,c[i].p.y+len);
}
}
if(!cnt)return 0;
sort(a+1,a+cnt+1);
double l=a[1].first,r=a[1].second,ans=0;
for(int i=2;i<=cnt;i++){
if(dcmp(a[i].first-r)<=0)r=r>a[i].second?r:a[i].second;
else ans+=r-l,l=a[i].first,r=a[i].second;
}
ans+=r-l;
return ans;
}
double simpson(double l,double r,double now,double fl,double fr,double fmid){
double mid=(l+r)/2,flmid=F((l+mid)/2),frmid=F((mid+r)/2);
double p=(fl+fmid+flmid*4)*(mid-l)/6,q=(fmid+fr+frmid*4)*(r-mid)/6;
if (dcmp(now-p-q)==0) return now;
else return simpson(l,mid,p,fl,fmid,flmid)+simpson(mid,r,q,fmid,fr,frmid);
}
void solve(){
sort(c+1,c+n+1);
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
if (dcmp(length(c[i].p-c[j].p)+c[i].r-c[j].r)<=0){
flag[i]=true;break;
}
}
}
int tot=0;
for(int i=1;i<=n;i++){
if(!flag[i]) c[++tot]=c[i];
}
n=tot;
double fl=F(Min),fr=F(Max),fmid=F((Min+Max)/2);
ans=simpson(Min,Max,(fl+fr+fmid*4)*(Max-Min)/6,fl,fr,fmid);
printf("%.3lf\n",ans);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) {
c[i].input();
double x1 = c[i].p.x-c[i].r,x2=c[i].p.x+c[i].r;
Min = Min<x1?Min:x1;
Max = Max>x2?Max:x2;
}
solve();
}
Part 1 结构体
- 点
#define Vector Point
//二维
struct Point {
double x, y;
Point(double x = 0,double y=0):x(x),y(y){}
bool operator < (Point o) {return dcmp(x-o.x)<0 || (dcmp(x-o.x)==0&&dcmp(y-o.y)<0);}
bool operator == (Point o) {return dcmp(x-o.x) == 0 && dcmp(y-o.y) == 0;}
Vector operator + (Vector o) {return Vector (x+o.x, y+o.y);}
Vector operator - (Point o) {return Vector(x-o.x,y-o.y);}
Vector operator * (double o) {return Vector(x*o,y*o);}
Vector operator / (double o) {return Vector(x/o,y/o);}
void input() {cin>>x>>y;}
void output() {printf("(%.10f,%.10f)",x,y);}
};
//K维
struct Point {
double x[20];int k;
Point(){k=0;}
Point(int _k,...){
k=_k;va_list ap;va_start (ap,_k);
for(int i=0;i<_k;i++) x[i]=va_arg(ap,double);
va_end(ap);
}
void input() {
if(k==0) {cout<<"Error k = 0"<<endl;exit(0);}
for(int i=0;i<k;i++) scanf("%lf",&x[i]);
}
void output() {
if(k==0){cout<<"Error k = 0"<<endl;exit(0);}
printf("(%.2f",x[0]);for(int i=1;i<k;i++)printf(",%.2f",x[i]);printf(")");
}
void safe(Point o){
if(k!=o.k) {
output();o.output();
cout<<"can't compare"<<endl;exit(0);
}
}
bool operator <(Point o){
safe(o);
for(int i=0;i<k;i++){
if(dcmp(x[i]-o.x[i])!=0)return dcmp(x[i]-o.x[i]<0)?1:0;
}return 0;
}
bool operator == (Point o) {
safe(o);
for(int i=0;i<k;i++) if(dcmp(x[i]-o.x[i])!=0)return 0;
return 1;
}
Vector operator +(Vector o) {
safe(o);Vector res;res.k=k;
for(int i=0;i<k;i++)res.x[i]=x[i]+o.x[i];
return res;
}
Vector operator -(Point o) {
safe(o);Vector res;res.k=k;
for(int i=0;i<k;i++)res.x[i]=x[i]-o.x[i];
return res;
}
Vector operator *(double o) {
Vector res;res.k=k;
for(int i=0;i<k;i++)res.x[i]=x[i]*o;
return res;
}
Vector operator /(double o) {
Vector res;res.k=k;
for(int i=0;i<k;i++)res.x[i]=x[i]/o;
return res;
}
};
向量和点用同一个结构体,但意义不同
- 直线
struct Line {
Point p;Vector v;double ang;
Line(){}
Line(Point _p,Vector _v) :p(_p),v(_v){v = v/(sqrt(v.x*v.x+v.y*v.y));ang = atan2(v.y,v.x);}
bool operator < (const Line& o) const{return ang < o.ang;}
Vector Normal(Vector A) {return Vector(-A.y / Length(A),A.x / Length(A));}
void move_line(double d) { p = p + Normal(v)*d;}
void output() {p.output();putchar(' ');v.output();putchar('\n');}
};
v为方向向量,在构造函数中会将其转化成单位向量
point 方法:已知求距离p点r单位有向距离的直线上的点
重载小于:按极角排序
- 圆
struct Circle{
Point o;double r;
Circle(){};
Circle(Point o,double r):o(o),r(r){}
Point point(double a){return Point(o.x + cos(a)*r, o.y + sin(a)*r);}
void input(){o.input();cin>>r;}
};
point方法:已知角度,求圆上的点
- 平面
struct Plane{
Point p;Vector n;
Plane(Point _p,Vector _n):p(_p),n(_n){}
};
Part 2 函数
Point(Vector) & Point(Vector)
- 点积
double Dot(Vector A,Vector B){return A.x*B.x + A.y*B.y;}
- 叉积
二维
double Cross(Vector A,Vector B){return A.x*B.y - A.y*B.x;}
三维
Vector Cross(Vector A,Vector B) {
return Vector(3,
A.x[1]*B.x[2]-A.x[2]*B.x[1],
A.x[2]*B.x[0]-A.x[0]*B.x[2],
A.x[0]*B.x[1]-A.x[1]*B.x[0]);
}
- 向量长度(两点相减)
double Length(Vector A) {return sqrt(Dot(A,A));}
- 两向量转角
double Angle(Vector A,Vector B) {return acos(Dot(A,B)/Length(A)/Length(B));}
- 向量极角[-PI,PI)
double Angle(Vector v){return atan2(v.y,v.x);}
- 向量旋转
Vector Rotate(Vector A, double rad){return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));}
- 法向量
Vector Normal (Vector A){return Vector(-A.y / Length(A),A.x / Length(A));}
- 异面直线p1+su和p2+tv的公垂线对应的s。如果平行/重合,返回inf
Rat GCXJD_Line_Line(Point p1,Point u,Point p2,Point v){
Rat b = Dot(u,u)*Dot(v,v)-Dot(u,v)*Dot(u,v);
if(b.fz==0) return Rat(inf);
Rat a = Dot(u,v)*Dot(v,p1-p2)-Dot(v,v)*Dot(u,p1-p2);
return Rat(a.fz,b.fz);
}
-
利用叉积点积判断向量位置
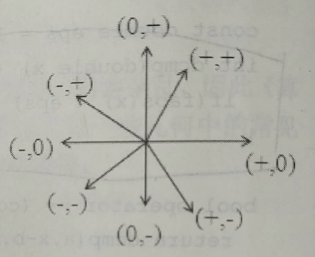
括号第一个数是点积符号,第二个数是叉积符号,第一个向量水平向右,表示了第二个向量的位置 -
三角形面积
二维
double Tri_Area(Point A,Point B,Point C){return Cross(B-A,C-A)/2;}
三维
double Area(Point A,Point B,Point C){
return Length(Cross(B-A,C-A))*0.5;
}
- 多边形面积(逆时针给点)
double PolygonArea(Point* p,int n){
double area = 0;
for(int i = 1; i < n-1; i++) area += Tri_Area(P[i],P[i+1],P[0]);
return area/2;
}
- 两点中点
Point Mid_Point_Point(Point A,Point B){return Point((A.x+B.x)/2,(A.y+B.y)/2);}
Point & Line
- 点到直线距离
double Point_Line_Dis(Point P,Line L){return fabs(Cross(L.v,P-L.p));}
- 点到线段距离
double Dis_Point_Seg(Point P,Point A,Point B){
if(A == B) return Length(P-A);
Vector v1 = B-A,v2 = P-A,v3 = P-B;
if(dcmp(Dot(v1,v2))<0) return Length(v2);
else if(dcmp(Dot(v1,v3))>0) return Length(v3);
else return Dis_Point_Line(P,A,B);
}
- 点到直线投影
Point TY_Point_Line(Point P,Line L){return A+L.v*Dot(L.v,P-A);}
Line & Line
- 两直线交点
Point JD_Line_Line(Line L1,Line L2){return L1.p+L1.v*(Cross(L2.v,L1.p-L2.p)/Cross(L1.v,L2.v));}
- 判断线段相交
两线段恰好有一个公共点,且不在任何一条线段的端点。
线段规范相交的充分条件是:每条线段的两个端点都在另一条线段的两侧
bool PDXJ_Seg_Seg(Point A1,Point A2,Point B1,Point B2){
double c1 = Cross(A2-A1,B1-A1),c2 = Corss(A2-A1,B2-A1),
c3 = Cross(B2-B1,A1-B1),c4 = Cross(B2-B1,A2-B1);
return dcmp(c1)*dcmp(c2) < 0 && dcmp(c3)*dcmp(c4) < 0;
}
如果允许在端点处相交,则还需要判断一个点是否在一条线段上(不包含端点)
bool PDON_Point_Seg(Point P,Point A1,Point A2){
return dcmp(Cross(A1-P,A2-P)) == 0 && dcmp(Dot(A1-P,A2-P)) < 0;
}
- 直线平移
Line Move_Line(double d){return Line(p+Normal(v)*d,v);}
Point & Circle
- 点到直线切线
int QX_Point_Circle(Point p,Circle C,Vector* v){
Vector u = C.c-p;
double dist = Length(u);
if(dist < C.r) return 0;
else if(dcmp(dist -C.r)){v[0] = Rotate(u,PI/2);return 1;}
else {
double ang = asin(C.r / dist);
v[0] = Rotate(u,-ang);v[1] = Rotate(u,ang);
return 2;
}
}
Line &Circle
- 直线与圆交点
int JD_Line_Circle(Line L,Circle C,vector<Point>& sol){
double a = L.v.x, b = L.p.x-C.o.x, c = L.v.y, d = L.p.y-C.o.y;
double e = a*a+c*c,f = 2*(a*b+c*d),g = b*b + d*d - C.r*C.r;
double delta = f*f-4*e*g,t1,t2;
if(dcmp(delta)<0) return 0;
if(dcmp(delta)==0){t1 = t2 = -f/(2*e);sol.push_back(L.point(t1));return 1;}
t1 = (-f-sqrt(delta))/(2*e);sol.push_back(L.point(t1));
t2 = (-f+sqrt(delta))/(2*e);sol.push_back(L.point(t2));
return 2;
}
Circle & Circle
- 两圆求交点
int JD_Circle_Circle(Circle C1,Circle C2,vector<Point>& sol)
{
double d=Length(C1.o-C2.o);//圆心距
if(dcmp(d)==0) return dcmp(C1.r-C2.r)==0 ? -1:0;//重合:包含
if(dcmp(C1.r + C2.r - d)<0) return 0;//相离
if(dcmp(fabs(C1.r-C2.r)-d)>0) return 0;//包含
double a = Angle(C2.o - C1.o);//圆心极角
double da = acos((C1.r*C1.r +d*d -C2.r*C2.r)/(2*C1.r*d));//余弦定理
Point p1 = C1.point(a-da),p2 = C1.point(a+da);
sol.push_back(p1);if(p1 == p2) return 1;
sol.push_back(p2);return 2;
}
- 两圆求切线
int Circle_Circle_Tangents(Circle A, Circle B, Point* a, Point* b){
int cnt=0;
if(A.r<B.r) { swap(A, B); swap(a, b); } //保证圆A比圆B大
int d2=(A.c.x-B.c.x)*(A.c.x-B.c.x)+(A.c.y-B.c.y)*(A.c.y-B.c.y);
int rdiff=A.r-B.r;
int rsum=A.r+B.r;
if(d2<rdiff*rdiff) return 0; //内含
double base=angle(B.c-A.c); // atan2(B.c.y-A.c.y,B.c.x-A.c.x);
if(d2==0&&A.r==B.r) return -1; //两圆重合,有无数条
if(d2==rdiff*rdiff){ //内切,一条切线
a[cnt]=A.point(base); b[cnt]=B.point(base); cnt++;
return 1;
}
//有外共切线
double ang=acos((A.r-B.r)/sqrt(d2));
a[cnt]=A.point(base+ang); b[cnt]=B.point(base+ang); cnt++;
a[cnt]=A.point(base-ang); b[cnt]=B.point(base-ang); cnt++;
if(d2==rsum*rsum){ //存在一条
a[cnt]=A.point(base); b[cnt]=B.point(PI+base); cnt++;
}
else if(d2>rsum*rsum){ //存在两条
double ang=acos((A.r+B.r)/sqrt(d2));
a[cnt]=A.point(base+ang); b[cnt]=B.point(PI+base+ang); cnt++;
a[cnt]=A.point(base-ang); b[cnt]=B.point(PI+base-ang); cnt++;
}
return cnt;
}
多边形
- 求凸包
vector<Point> ConvexHull(vector<Point> p) {
sort(p.begin(), p.end());
p.erase(unique(p.begin(), p.end()), p.end());
int n = p.size();
int m = 0;
vector<Point> ch(n+1);
for(int i = 0; i < n; i++) {
while(m > 1 && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;
ch[m++] = p[i];
}
int k = m;
for(int i = n-2; i >= 0; i--) {
while(m > k && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;
ch[m++] = p[i];
}
if(n > 1) m--;
ch.resize(m);
return ch;
}
- 旋转卡壳
double rotate_calipers(vector<Point>ch,int n)
{
double ans=-0x7fffffff;
ch.push_back(ch[0]);
int q=1;
for(int i=0;i<n;i++){
while(Cross(ch[q]-ch[i+1],ch[i]-ch[i+1])<Cross(ch[q+1]-ch[i+1],ch[i]-ch[i+1]))
q = (q+1)%n;
ans=max(ans,max(length(ch[q]-ch[i]),length(ch[q+1]-ch[i+1])));
}
return ans;
}
平面
- 三点确定一个平面
- 点到平面距离
double Dis_Point_Plane(Point p,Plane p0){
return fabs(Dot(p-p0.p,p0.n));//不取绝对值得到的是有向距离
}
- 点到平面投影
Point TY_Point_Plane(Point p,Plane p0){
return p-p0.n*Dot(p-p0.p,p0.n);
}
- 线和平面求交点
直线
Point JD_Line_Plane(Point p1,Point p2,Plane p){
Vector v=p2-p1;
if(dcmp(Dot(p.n,p2-p1)==0)){
cout<<"find JD Error"<<endl;exit(0);
}
double t=(Dot(p.n,p.p-p1)/Dot(p.n,p2-p1));
return p1+v*t;
}
线段
Point JD_Seg_Plane(Point p1,Point p2,Plane p){
Vector v=p2-p1;
if(dcmp(Dot(p.n,p2-p1)==0)){
cout<<"find JD Error "<<endl;
exit(0);
}
double t=(Dot(p.n,p.p-p1)/Dot(p.n,p2-p1));
if(dcmp(t-1)>0||dcmp(t-0)<0){
cout<<"find JD Error"<<endl;exit(0);
}
return p1+v*t;
}
- 半平面交
bool on_l(Line L,Point p) {
return Cross(L.v, p-L.p)>0;
}
int BPMJ(Line* L, int n, Point* poly) {
sort(L,L+n);
int ll, rr;
Point *p = new Point[n];
Line *q = new Line[n];
q[ll=rr=0] = L[0];
for(int i = 1; i < n; i++) {
while(ll < rr && !on_l(L[i], p[rr-1])) rr--;
while(ll < rr && !on_l(L[i], p[ll])) ll++;
q[++rr] = L[i];
if(fabs(Cross(q[rr].v, q[rr-1].v)) < eps) {
rr--;
if(on_l(q[rr], L[i].p)) q[rr] = L[i];
}
if(ll < rr) p[rr-1] = JD_Line_Line(q[rr-1], q[rr]);
}
while(ll < rr && !on_l(q[ll], p[rr-1])) rr--;
if(rr - ll <= 1) return 0;
p[rr] = JD_Line_Line(q[rr],q[ll]);
int m = 0;
for(int i = ll;i <= rr;i++) poly[m++] = p[i];
return m;
}

