Numerical methods in enginering with python3 (1)

Numerical methods in enginering with python3 (1)

1Numpy 库

1.1Numpy中的矩阵函数

  1. np.diagonal(A) 返回由A中的主对角元素组成的一维矩阵
  2. np.diagonal(A,1) 返回由A中的第一副对角元素组成的一维矩阵
  3. np.trace(A) 返回A中的主对角元素的和
  4. np.argmax(A,axis= 0) 在0轴上，最小的数
  5. np.identity(3) 返回3维的单位矩阵
  6. np.dot(a,b)
    常用的：
  • 若a,b均为行矩阵，则返回其内积（对应元素相乘，最后再相加，返回值为标量）
  • 若a,b均为n维矩阵，则返回a,b的矩阵的乘法
  • 若a为n维，b为行矩阵，则返回矩阵中的每一个元素，为a矩阵的某行的各个元素与b矩阵的对应元素相乘，再相加。（类似于矩阵的乘法，不过不是行、列乘的关系，而是行行乘）
  1. np.inner(a,b)
    常用的
  • 若a,b均为行矩阵，则返回其内积（对应元素相乘，最后再相加，返回值为标量）
  • 若a,b均为n维矩阵，则返回矩阵中的每一个元素，为a矩阵的某行的各个元素与b矩阵某行的对应元素相乘，再相加得到的（类似于矩阵的乘法，不过不是行、列乘的关系，而是行行乘）
  1. np.outer(a,b) 返回a,b中所有元素对的乘积组成的矩阵
  2. a*b a与b的维度必须一样，返回的是对应元素相乘得到的矩阵

1.2线性代数模块

from numpy.linalg import inv,solve

  1. 矩阵的逆 inv(A)
  2. 求解Ax = b方程中的x solve(A,b)

1.3深复制矩阵

不是创建矩阵的视图，而是新创建一个对象
b = a.copy()

1.4矩阵的向量化操作

数学中这样的语句:

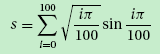
在numpy中可以写为：
'''

计算更快，但是内存用的多

import numpy as np
from math import pi
x= np.arange(0.0,1.001pi,0.01pi)
print(sum(np.sqrt(x)np.sin(x)))
'''

2线性代数方程组

解决联立方程组 Ax = b

2.1代数方程组的形式


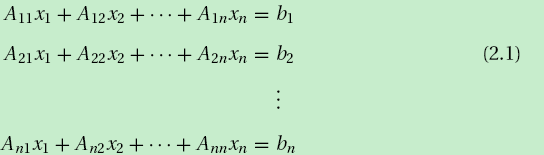
系数矩阵Aij和常量bj已知，未知量为xi
在矩阵的记法中，方程组被写为：

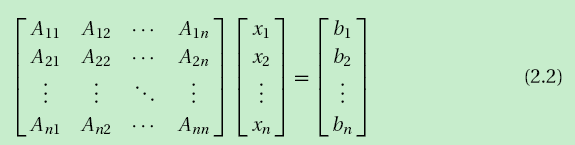
或简化为：

增广矩阵为：

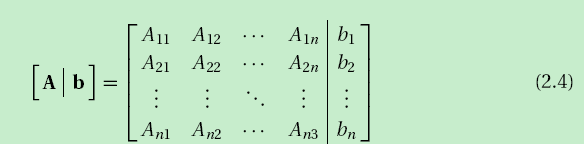
2.2条件

  1. 矩阵的范数
    描述矩阵的“大小”，符号为

2范数：

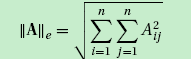
无穷范数：

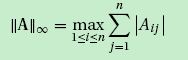
2. 条件数
条件数是线性方程组Ax=b的解对b中的误差或不确定度的敏感性的度量。矩阵计算对于误差的敏感性。对于线性方程组Ax=b，如果A的条件数大，b的微小改变就能引起解x较大的改变，数值稳定性差。如果A的条件数小，b有微小的改变，x的改变也很微小，数值稳定性好。它也可以表示b不变，而A有微小改变时，x的变化情况。若条件数接近1，则方程组是良态的。

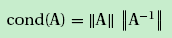
2.3. 线性方程组的解法
线性方程组的解法有两种：直接法与迭代法
直接法常用于解决低阶稠密矩阵（150阶左右），迭代法常用于解决大型稀疏稠密矩阵

posted @ 2019-08-25 14:13  随想LJG  阅读(288)  评论(0)  编辑  收藏  举报