[LeetCode] 790. Domino and Tromino Tiling 多米诺和三格骨牌

You have two types of tiles: a 2 x 1 domino shape and a tromino shape. You may rotate these shapes.

Given an integer n, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo 109 + 7.

In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

Example 1:

Input: n = 3
Output: 5
Explanation: The five different ways are show above.

Example 2:

Input: n = 1
Output: 1

Constraints:

1 <= n <= 1000

这道题是关于多米诺骨牌和三格骨牌的，其中由两个方形格子组成的是多米诺骨牌（音译，即为双格骨牌），而由三个方形格子组成的‘L’型的是三格骨牌，但其实本质还是个拼格子的问题，并没有利用到骨牌酷炫的连倒技能，倒反而更像是俄罗斯方块中的形状。说是有一个2xN大小的棋盘，我们需要用这些多米诺和三格骨牌来将棋盘填满，问有多少种不同的填充方法，结果需要对一个超大数取余。那么根据博主多年的经验，对于这种求极值，并且超大的情况下，只能使用动态规划 Dynamic Programming 来做，什么暴力递归神马的，等着爆栈吧。

既然决定了要用 DP 来做，那么首先就来设计 dp 数组吧，这里就用一个一维的 dp 数组就行了，其中 dp[i] 表示填满前i列的不同填法总数对超大数 10e^9+7 取余后的结果。DP 解法的难点就是求状态转移方程了，没什么太好的思路的时候，就从最简单的情况开始罗列吧。题目中给了N的范围是 [1, 1000]，那么来看：

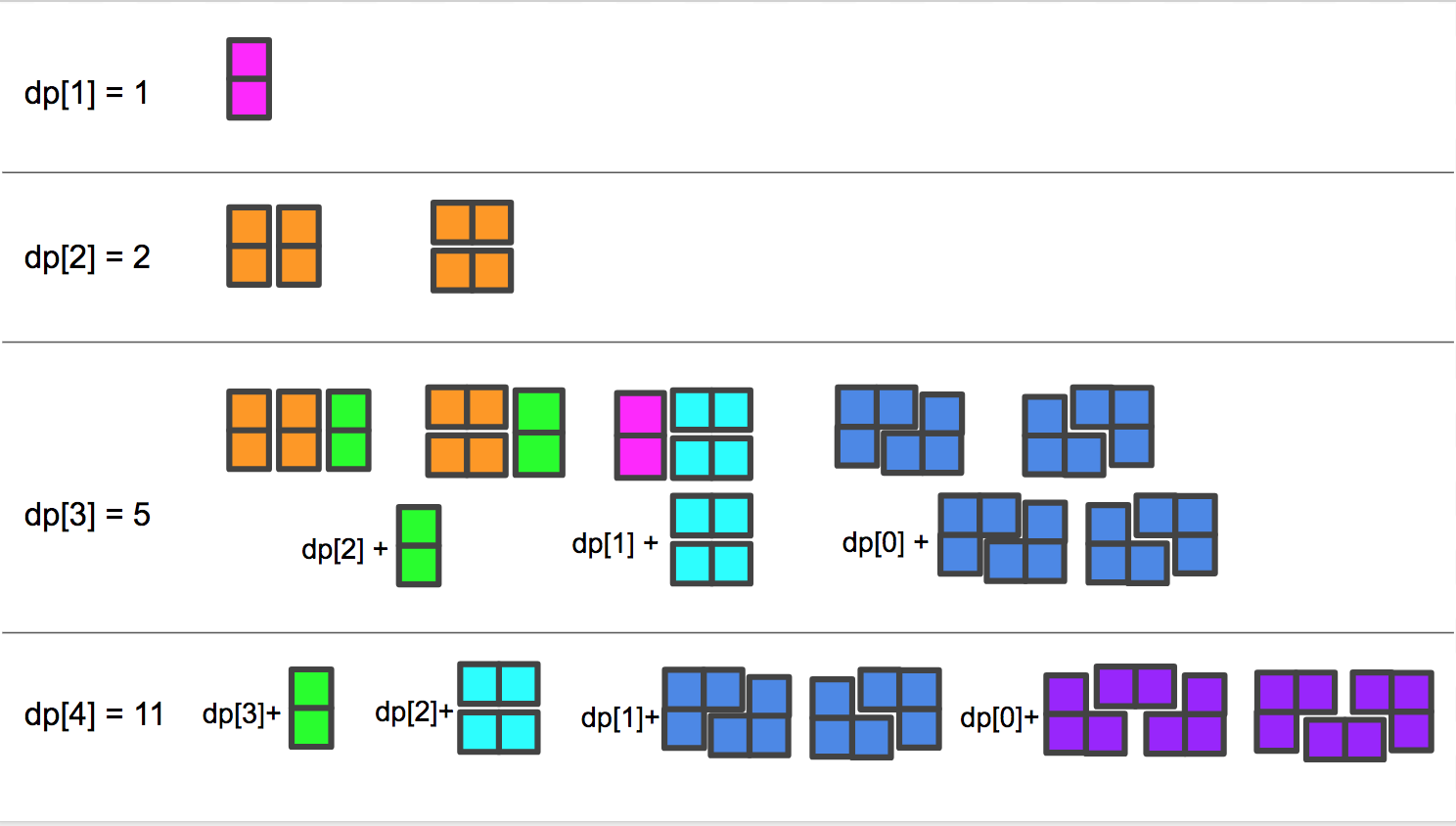
当 N=1 时，那么就是一个 2x1 大小的棋盘，只能放一个多米诺骨牌，只有一种情况。

当 N=2 时，那么就是一个 2x2 大小的棋盘，如下图所示，有两种放置方法，可以将两个多米诺骨牌竖着并排放，或者是将其横着并排放。

当 N=3 时，那么就是一个 3x2 大小的棋盘，共用五种放置方法，如下图所示。仔细观察这五种情况，可以发现其时时跟上面的情况有联系的。前两种情况其实是 N=2 的两种情况后面加上了一个竖着的多米诺骨牌，第三种情况其实是 N=1 的那种情况后面加上了两个平行的横向的多米诺骨牌，后两种情况是 N=0（空集）再加上两种三格骨牌对角摆开的情况。

当 N=4 时，那么就是一个 4x2 大小的棋盘，共用十一种放置方法，太多了就不一一画出来了，但是其也是由之前的情况组合而成的。首先是 N=3 的所有情况后面加上一个竖着多米诺骨牌，然后是 N=2 的所有情况加上两个平行的横向的多米诺骨牌，然后 N=1 再加上两种三格骨牌对角摆开的情况，然后 N=0（空集）再加上两种三格骨牌和一个横向多米诺骨牌组成的情况。

N=5 的情况博主没有再画了，可以参见ZhengKaiWei大神的帖子中的手稿图，很萌～

根据目前的状况，我们可以总结一个很重要的规律，就是 dp[n] 是由之前的 dp 值组成的，其中 dp[n-1] 和 dp[n-2] 各自能贡献一种组成方式，而 dp[n-3]，一直到 dp[0]，都能各自贡献两种组成方式，所以状态转移方程呼之欲出：

dp[n] = dp[n-1] + dp[n-2] + 2 * (dp[n-3] + ... + dp[0])

= dp[n-1] + dp[n-3] + dp[n-2] + dp[n-3] + 2 * (dp[n-4] + ... dp[0])

= dp[n-1] + dp[n-3] + dp[n-1]

= 2 * dp[n-1] + dp[n-3]

最后化简后的形式就是最终的状态转移方程了，是不是叼的飞起～

class Solution {
public:
    int numTilings(int N) {
        if (N < 2) return 1;
        int M = 1e9 + 7;
        vector<long> dp(N + 1);
        dp[0] = 1; dp[1] = 1; dp[2] = 2;
        for (int i = 3; i <= N; ++i) {
            dp[i] = (dp[i - 1] * 2 + dp[i - 3]) % M;
        }
        return dp[N];
    }
};