[LeetCode] 668. Kth Smallest Number in Multiplication Table 乘法表中的第K小的数字

Nearly everyone has used the Multiplication Table. The multiplication table of size m x n is an integer matrix mat where mat[i][j] == i * j (1-indexed).

Given three integers m, n, and k, return the kth smallest element in the m x n multiplication table.

Example 1:

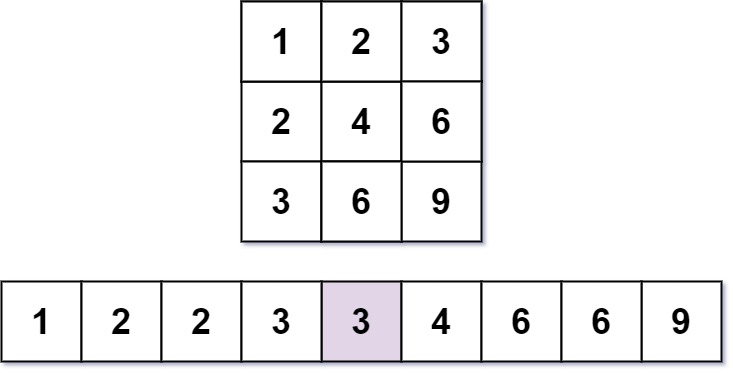
Input: m = 3, n = 3, k = 5
Output: 3
Explanation: The 5th smallest number is 3.

Example 2:

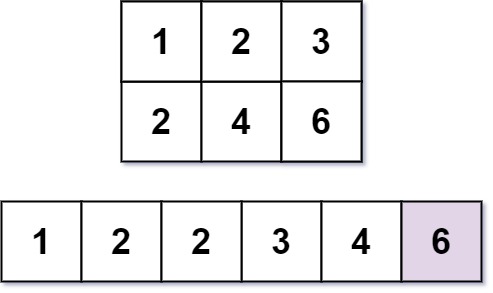
Input: m = 2, n = 3, k = 6
Output: 6
Explanation: The 6th smallest number is 6.

Constraints:

1 <= m, n <= 3 * 104
1 <= k <= m * n

这道题跟之前那道 Kth Smallest Element in a Sorted Matrix 没有什么太大的区别，这里的乘法表也是各行各列分别有序的。那么之前帖子里的方法都可以拿来参考。之前帖子中的解法一在这道题中无法通过 OJ，维护一个大小为k的优先队列实在是没有利用到这道题乘法表的特点，但是后两种解法都是可以的。为了快速定位出第K小的数字，这里采用二分搜索法，由于是有序矩阵，那么左上角的数字一定是最小的，而右下角的数字一定是最大的，所以这个是搜索的范围，然后算出中间数字 mid，由于矩阵中不同行之间的元素并不是严格有序的，所以要在每一行都查找一下 mid，由于乘法表每行都是连续数字 1，2，3...乘以当前行号（从1开始计数），所以甚至不需要在每行中使用二分查找，而是直接定位出位置。具体做法是，先比较 mid 和该行最后一个数字的大小，最后一数字是 n * i，i是行数，n是该行数字的个数，如果 mid 大的话，直接将该行所有数字的个数加入 cnt，否则的话加上 mid / i，比如当前行是 2, 4, 6, 8, 10，如果要查找小于7的个数，那么就是7除以2，得3，就是有三个数小于7，直接加入 cnt 即可。这样就可以快速算出矩阵中所有小于 mid 的个数，根据 cnt 和k的大小关系，来更新范围，循环推出后，left 就是第K小的数字，参见代码如下：

解法一：

 class Solution {
 public:
     int findKthNumber(int m, int n, int k) {
         int left = 1, right = m * n;
         while (left < right) {
             int mid = left + (right - left) / 2, cnt = 0;
             for (int i = 1; i <= m; ++i) {
                 cnt += (mid > n * i) ? n : (mid / i);
             }
             if (cnt < k) left = mid + 1;
             else right = mid;
         }
         return right;
     }
 };

下面这种解法在统计小于 mid 的数字个数的方法上有些不同，并不是逐行来统计，而是从左下角的数字开始统计，如果该数字小于 mid，说明该数字及上方所有数字都小于 mid，cnt 加上i个，然后向右移动一位继续比较。如果当前数字小于 mid 了，那么向上移动一位，直到横纵方向有一个越界停止，其他部分都和上面的解法相同，参见代码如下：

解法二：

 class Solution {
 public:
     int findKthNumber(int m, int n, int k) {
         int left = 1, right = m * n;
         while (left < right) {
             int mid = left + (right - left) / 2, cnt = 0, i = m, j = 1;
             while (i >= 1 && j <= n) {
                 if (i * j <= mid) {
                     cnt += i;
                     ++j;
                 } else {
                     --i;
                 }
             }
             if (cnt < k) left = mid + 1;
             else right = mid;
         }
         return right;
     }
 };

下面这种解法由网友 bambu 提供，是对解法二的优化，再快一点，使用除法来快速定位新的j值，然后迅速算出当前行的小于 mid 的数的个数，然后快速更新i的值，这比之前那种一次只加1或减1的方法要高效许多，感觉像是解法一和解法二的混合体，参见代码如下：

解法三：

 class Solution {
 public:
     int findKthNumber(int m, int n, int k) {
        int left = 1, right = m * n;
        while (left < right) {
            int mid = left + (right - left) / 2, cnt = 0, i = m, j = 1;
            while (i >= 1 && j <= n) {
                 int t = j;
                 j = (mid > n * i) ? n + 1 : (mid / i + 1);
                 cnt += (j - t) * i;
                 i = mid / j;
             }
            if (cnt < k) left = mid + 1;
            else right = mid;
        }
        return right;
     }
 };