[LeetCode] Freedom Trail 自由之路

 

In the video game Fallout 4, the quest "Road to Freedom" requires players to reach a metal dial called the "Freedom Trail Ring", and use the dial to spell a specific keyword in order to open the door.

Given a string ring, which represents the code engraved on the outer ring and another string key, which represents the keyword needs to be spelled. You need to find the minimum number of steps in order to spell all the characters in the keyword.

Initially, the first character of the ring is aligned at 12:00 direction. You need to spell all the characters in the string key one by one by rotating the ring clockwise or anticlockwise to make each character of the string key aligned at 12:00 direction and then by pressing the center button. 
At the stage of rotating the ring to spell the key character key[i]:

1. You can rotate the ring clockwise or anticlockwise one place, which counts as 1 step. The final purpose of the rotation is to align one of the string ring's characters at the 12:00 direction, where this character must equal to the character key[i].
2. If the character key[i] has been aligned at the 12:00 direction, you need to press the center button to spell, which also counts as 1 step. After the pressing, you could begin to spell the next character in the key (next stage), otherwise, you've finished all the spelling.

 

Example:

 

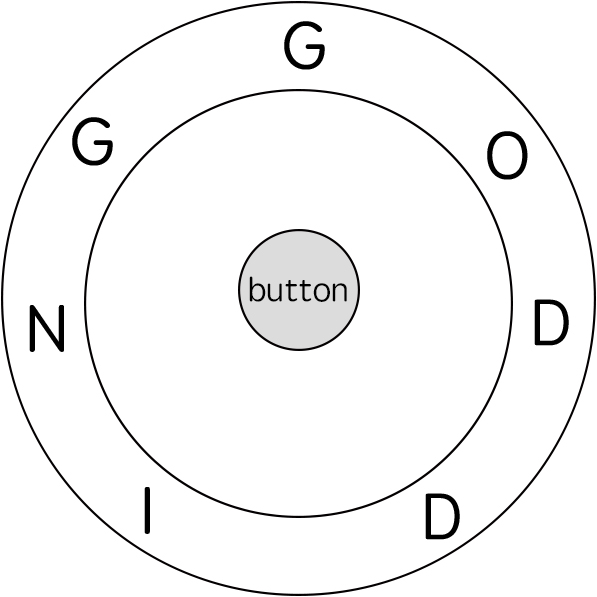
Input: ring = "godding", key = "gd"
Output: 4
Explanation:
 For the first key character 'g', since it is already in place, we just need 1 step to spell this character. 
 For the second key character 'd', we need to rotate the ring "godding" anticlockwise by two steps to make it become "ddinggo".
 Also, we need 1 more step for spelling.
 So the final output is 4.

 

Note:

1. Length of both ring and key will be in range 1 to 100.
2. There are only lowercase letters in both strings and might be some duplcate characters in both strings.
3. It's guaranteed that string key could always be spelled by rotating the string ring.

 

这道题是关于辐射4这款游戏出的，博主虽然没有玩过这款游戏，但是知道确实有些游戏中需要破解一些谜题才能继续通关，像博主很早以前玩过的恐龙危机啊，生化危机啊啥的，都有一些机关需要破解，博主大部分都要靠看攻略来通关哈哈。这道题讲的是一种叫做自由之路的机关，我们需要将密码字符串都转出来，让我们求最短的转动步数。博主最先尝试的用贪婪算法来做，就是每一步都选最短的转法，但是OJ中总有些test case会引诱贪婪算法得出错误的结果，因为全局最优解不一定都是局部最优解，而贪婪算法一直都是在累加局部最优解，这也是为啥DP解法这么叼的原因。贪婪算法好想好实现，但是不一定能得到正确的结果。DP解法难想不好写，但往往才是正确的解法，这也算一个trade off吧。这道题可以用DP来解，难点还是写递推公式，博主在充分研究网上大神们的帖子后尝试着自己理理思路，如果有不正确或者不足的地方，也请各位不吝赐教。此题需要使用一个二维数组dp，其中dp[i][j]表示转动从i位置开始的key串所需要的最少步数(这里不包括spell的步数，因为spell可以在最后统一加上)，此时表盘的12点位置是ring中的第j个字符。不得不佩服这样的设计的确很巧妙，我们可以从key的末尾往前推，这样dp[0][0]就是我们所需要的结果，因为此时是从key的开头开始转动，而且表盘此时的12点位置也是ring的第一个字符。现在我们来看如何找出递推公式，对于dp[i][j]，我们知道此时要将key[i]转动到12点的位置，而此时表盘的12点位置是ring[j]，我们有两种旋转的方式，顺时针和逆时针，我们的目标肯定是要求最小的转动步数，而顺时针和逆时针的转动次数之和刚好为ring的长度n，这样我们求出来一个方向的次数，就可以迅速得到反方向的转动次数。为了将此时表盘上12点位置上的ring[j]转动到key[i]，我们要将表盘转动一整圈，当转到key[i]的位置时，我们计算出转动步数diff，然后计算出反向转动步数，并取二者较小值为整个转动步数step，此时我们更新dp[i][j]，更新对比值为step + dp[i+1][k]，这个也不难理解，因为key的前一个字符key[i+1]的转动情况suppose已经计算好了，那么dp[i+1][k]就是当时表盘12点位置上ring[k]的情况的最短步数，step就是从ring[k]转到ring[j]的步数，也就是key[i]转到ring[j]的步数，用语言来描述就是，从key的i位置开始转动并且此时表盘12点位置为ring[j]的最小步数(dp[i][j])就等价于将ring[k]转动到12点位置的步数(step)加上从key的i+1位置开始转动并且ring[k]已经在表盘12点位置上的最小步数(dp[i+1][k])之和。突然发现这不就是之前那道Reverse Pairs中解法一中归纳的顺序重现关系的思路吗，都做了总结，可换个马甲就又不认识了，泪目中。。。

 

解法一：

class Solution {
public:
    int findRotateSteps(string ring, string key) {
        int n = ring.size(), m = key.size();
        vector<vector<int>> dp(m + 1, vector<int>(n));
        for (int i = m - 1; i >= 0; --i) {
            for (int j = 0; j < n; ++j) {
                dp[i][j] = INT_MAX;
                for (int k = 0; k < n; ++k) {
                    if (ring[k] == key[i]) {
                        int diff = abs(j - k);
                        int step = min(diff, n - diff);
                        dp[i][j] = min(dp[i][j], step + dp[i + 1][k]);
                    }
                }
            }
        }
        return dp[0][0] + m;      
    }
};

 

下面这种解法是用DFS来解的，我们需要做优化，也就是用memo数组来保存已经计算过的结果，否则大量的重复运算是无法通过OJ的。其实这里的memo数组也起到了跟上面解法中的dp数组相类似的作用，还有就是要注意数组v的作用，记录了每个字母在ring中的出现位置，由于ring中可能有重复字符，而且麻烦的情况是当前位置向两个方向分别转动相同的步数会分别到达两个相同的字符，这也是贪婪算法会失效的一个重要原因，而且也是上面的解法在找到ring[k] == key[i]并处理完之后不break的原因，因为后面还有可能找到。上面的迭代解法中使用到的变量i和j可以直接访问到，而在递归的写法中必须要把位置变量x和y当作参数导入进去，这样才能更新正确的地方，参见代码如下：

 

解法二：

class Solution {
public:
    int findRotateSteps(string ring, string key) {
        int n = ring.size(), m = key.size();
        vector<vector<int>> v(26);
        vector<vector<int>> memo(n, vector<int>(m));
        for (int i = 0; i < n; ++i) v[ring[i] - 'a'].push_back(i);
        return helper(ring, key, 0, 0, v, memo);
    }
    int helper(string ring, string key, int x, int y, vector<vector<int>>&v, vector<vector<int>>& memo) {
        if (y == key.size()) return 0;
        if (memo[x][y]) return memo[x][y];
        int res = INT_MAX, n = ring.size();
        for (int k : v[key[y] - 'a']) {
            int diff = abs(x - k);
            int step = min(diff, n - diff);
            res = min(res, step + helper(ring, key, k, y + 1, v, memo));
        }
        return memo[x][y] = res + 1;
    }
};

 

参考资料：

https://discuss.leetcode.com/topic/81684/concise-java-dp-solution

https://discuss.leetcode.com/topic/82720/evolve-from-brute-force-to-dp

 

LeetCode All in One 题目讲解汇总(持续更新中...)