[LeetCode] 351. Android Unlock Patterns 安卓解锁模式
Given an Android 3x3 key lock screen and two integers m and n, where 1 ≤ m ≤ n ≤ 9, count the total number of unlock patterns of the Android lock screen, which consist of minimum of m keys and maximum n keys.
Rules for a valid pattern:
- Each pattern must connect at least m keys and at most n keys.
- All the keys must be distinct.
- If the line connecting two consecutive keys in the pattern passes through any other keys, the other keys must have previously selected in the pattern. No jumps through non selected key is allowed.
- The order of keys used matters.
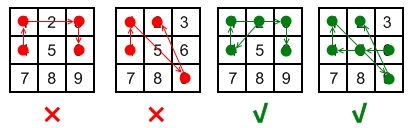
Explanation:
| 1 | 2 | 3 | | 4 | 5 | 6 | | 7 | 8 | 9 |
Invalid move: 4 - 1 - 3 - 6
Line 1 - 3 passes through key 2 which had not been selected in the pattern.
Invalid move: 4 - 1 - 9 - 2
Line 1 - 9 passes through key 5 which had not been selected in the pattern.
Valid move: 2 - 4 - 1 - 3 - 6
Line 1 - 3 is valid because it passes through key 2, which had been selected in the pattern
Valid move: 6 - 5 - 4 - 1 - 9 - 2
Line 1 - 9 is valid because it passes through key 5, which had been selected in the pattern.
Example:
Input: m = 1, n = 1
Output: 9
Credits:
Special thanks to @elmirap for adding this problem and creating all test cases.
这道题乍一看题目这么长以为是一个设计题,其实不是,这道题还是比较有意思的,起码跟实际结合的比较紧密。这道题说的是安卓机子的解锁方法,有9个数字键,如果密码的长度范围在 [m, n] 之间,问所有的解锁模式共有多少种,注意题目中给出的一些非法的滑动模式。那么先来看一下哪些是非法的,首先1不能直接到3,必须经过2,同理的有4到6,7到9,1到7,2到8,3到9,还有就是对角线必须经过5,例如1到9,3到7等。建立一个二维数组 jumps,用来记录两个数字键之间是否有中间键,然后再用一个一位数组 visited 来记录某个键是否被访问过,然后用递归来解,先对1调用递归函数,在递归函数中,遍历1到9每个数字 next,然后找他们之间是否有 jump 数字,如果 next 没被访问过,并且 jump 为0,或者 jump 被访问过,对 next 调用递归函数。数字1的模式个数算出来后,由于 1,3,7,9 是对称的,所以乘4即可,然后再对数字2调用递归函数,2,4,6,9 也是对称的,再乘4,最后单独对5调用一次,然后把所有的加起来就是最终结果了,参见代码如下:
解法一:
class Solution { public: int numberOfPatterns(int m, int n) { int res = 0; vector<bool> visited(10, false); vector<vector<int>> jumps(10, vector<int>(10, 0)); jumps[1][3] = jumps[3][1] = 2; jumps[4][6] = jumps[6][4] = 5; jumps[7][9] = jumps[9][7] = 8; jumps[1][7] = jumps[7][1] = 4; jumps[2][8] = jumps[8][2] = 5; jumps[3][9] = jumps[9][3] = 6; jumps[1][9] = jumps[9][1] = jumps[3][7] = jumps[7][3] = 5; res += helper(1, 1, m, n, jumps, visited, 0) * 4; res += helper(2, 1, m, n, jumps, visited, 0) * 4; res += helper(5, 1, m, n, jumps, visited, 0); return res; } int helper(int num, int len, int m, int n, vector<vector<int>>& jumps, vector<bool>& visited, int res) { if (len >= m) ++res; ++len; if (len > n) return res; visited[num] = true; for (int next = 1; next <= 9; ++next) { int jump = jumps[num][next]; if (!visited[next] && (jump == 0 || visited[jump])) { res = helper(next, len, m, n, jumps, visited, res); } } visited[num] = false; return res; } };
下面这种方法很简洁,但是不容易理解,讲解请看这个帖子。其中 used 是一个9位的 mask,每位对应一个数字,如果为1表示存在,0表示不存在,(i1, j1) 是之前的位置,(i, j) 是当前的位置,所以滑动是从 (i1, j1) 到 (i, j),中间点为 ((i1+i)/2, (j1+j)/2),这里的I和J分别为 i1+i 和 j1+j,还没有除以2,所以I和J都是整数。如果 I%2 或者 J%2 不为0,说明中间点的坐标不是整数,即中间点不存在,如果中间点存在,如果中间点被使用了,则这条线也是成立的,可以调用递归,参见代码如下:
解法二:
class Solution { public: int numberOfPatterns(int m, int n) { return count(m, n, 0, 1, 1); } int count(int m, int n, int used, int i1, int j1) { int res = m <= 0; if (!n) return 1; for (int i = 0; i < 3; ++i) { for (int j = 0; j < 3; ++j) { int I = i1 + i, J = j1 + j, used2 = used | (1 << (i * 3 + j)); if (used2 > used && (I % 2 || J % 2 || used2 & (1 << (I / 2 * 3 + J / 2)))) { res += count(m - 1, n - 1, used2, i, j); } } } return res; } };
Github 同步地址:
https://github.com/grandyang/leetcode/issues/351
参考资料:
https://leetcode.com/problems/android-unlock-patterns/










【推荐】还在用 ECharts 开发大屏?试试这款永久免费的开源 BI 工具!
【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步