[LeetCode] 119. Pascal's Triangle II 杨辉三角之二

Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal's triangle.

Note that the row index starts from 0.

In Pascal's triangle, each number is the sum of the two numbers directly above it.

Example:

Input: 3
Output: [1,3,3,1]

Follow up:

Could you optimize your algorithm to use only O(k) extra space?

杨辉三角想必大家并不陌生，应该最早出现在初高中的数学中，其实就是二项式系数的一种写法。

　　　　　　　　１
　　　　　　　１　１
　　　　　　１　２　１
　　　　　１　３　３　１
　　　　１　４　６　４　１
　　　１　５　10　10　５　１
　　１　６　15　20　15　６　１
　１　７　21　35　35　21　７　１
１　８　28　56　70　56　28　８　１

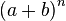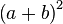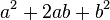杨辉三角形第n层（顶层称第0层，第1行，第n层即第 n+1 行，此处n为包含0在内的自然数）正好对应于二项式 $\left(a+b\right)^{n}$ 展开的系数。例如第二层 1 2 1 是幂指数为2的二项式 $\left(a+b\right)^{2}$ 展开形式 $a^{2}+2ab+b^{2}$ 的系数。

杨辉三角主要有下列五条性质：

杨辉三角以正整数构成，数字左右对称，每行由1开始逐渐变大，然后变小，回到1。
第 $n$ 行的数字个数为 $n$ 个。
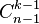第 $n$ 行的第 $k$ 个数字为组合数 $C_{n-1}^{k-1}$ 。
第 $n$ 行数字和为 $2^{n-1}$ 。
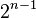除每行最左侧与最右侧的数字以外，每个数字等于它的左上方与右上方两个数字之和（也就是说，第 $n$ 行第 $k$ 个数字等于第 $n-1$ 行的第 $k-1$ 个数字与第 $k$ 个数字的和）。这是因为有组合恒等式： $C_{n}^{i}=C_{n-1}^{i-1}+C_{n-1}^{i}$ 。可用此性质写出整个杨辉三角形。

由于题目有额外限制条件，程序只能使用 O(k) 的额外空间，那么这样就不能把每行都算出来，而是要用其他的方法, 我最先考虑用的是第三条性质，算出每个组合数来生成第n行系数，代码请参见评论区一楼。本地调试输出前十行，没啥问题，拿到 OJ 上测试，程序在第 18 行跪了，中间有个系数不正确。那么问题出在哪了呢，仔细找找，原来出在计算组合数那里，由于算组合数时需要算连乘，而整型数 int 的数值范围只有 -32768 到 32768 之间，那么一旦n值过大，连乘肯定无法计算。而丧心病狂的 OJ 肯定会测试到成百上千行，所以这个方法不行。那么我们再来考虑利用第五条性质，除了第一个和最后一个数字之外，其他的数字都是上一行左右两个值之和。那么我们只需要两个 for 循环，除了第一个数为1之外，后面的数都是上一次循环的数值加上它前面位置的数值之和，不停地更新每一个位置的值，便可以得到第n行的数字，具体实现代码如下：

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> res(rowIndex + 1);
        res[0] = 1;
        for (int i = 1; i <= rowIndex; ++i) {
            for (int j = i; j >= 1; --j) {
                res[j] += res[j - 1];
            }
        }
        return res;
    }
};