清北学堂2019.7.18 & 清北学堂2019.7.19
Day 6 钟皓曦
经典题目:石子合并
可以合并任意两堆,代价为数量的异或(^)和
f[s]把s的二进制所对应石子合并成一堆所花代价
枚举s的子集
#include<iostream> using namespace std; int main() { cin >> n; for (int a=0;a<n;a++) cin >> z[a]; for (int a=0;a<(1<<n);a++) for (int b=0;b<n;b++) if (a & (1<<b)) sum[a] += z[b]; memset(f,0x3f,sizeof(f)); for (int a=0;a<n;a++) f[1<<a] = 0; for (int s=0;s<(1<<n);s++) for (int a=1;a<s;a++) if ( (s|a) == s) f[s] = min(f[s],f[a]+f[a^s]+(sum[a]^sum[a^s])); for (int s=0;s<(1<<n);s++) for (int a=(s-1)&s;a;a=(a-1)&s) f[s] = min(f[s],f[a]+f[a^s]+(sum[a]^sum[a^s])); cout << f[(1<<n)-1] << endl; }
然后今天的正题就是博弈论dp了【nim游戏:据说80%的博弈论dp最终都会转化到nim游戏上来】
其实这种题型只与Alice和Bob有关(大雾
这种东西大概是这样的
有一个游戏g,有两个人Alice和Bob在Van它,是回合制游戏,该游戏无平局,胜负条件:当某个人无法操作时就输了
下面以好多好多的题来说明
T1
有一个整数S(2<=S<=200),先手在S上减掉一个数x,至少是1,但小于S。之后双方轮流把S减掉一个正整数,但都不能超过先前一回合对方减掉的数的k倍,减到0的一方获胜。问先手是否必胜?
solution:
从一个状态转到另外一种状态,会有必败态和必胜态出现
f[s] s->false 必报 s->true 必胜
状态由s->s1.s2.s3······
若对于任意的f[si]=true则走向了必胜态。
直接记忆化搜索!
dp[i][j]表示当前剩下的数为i,最多能减的数为j的状态,dp[i][j] = = 1必胜,否则必败
dp[i][j]->dp[i-x][x*k](1<=x<=j)
如果对于某个x, dp[i-x][x*k] = = 0,则dp[i][j]=1,否则dp[i][j]=0
要求的为dp[S][S-1]
O(S^3)
f[i][j]还剩下i,对手上一轮减的数字是j,此时自己是必胜态还是必败态【伪代码】
#include<iostream> using namespace std; bool f[][],g[][]; bool dfs(int i,int j) { if (i==0) return false; if (g[i][j]) return f[i][j]; g[i][j]=true;f[i][j]=false; for (int r=1;r<=i && r<=k*j;r++) if (dfs(i-r,r) == false) f[i][j]=true; return f[i][j]; } int main() { cin >> s >> k; for (int a=1;a<s;a++) if (dfs(s-a,a) == false) { cout << "Alice" << endl; return 0; } cout << "Bob" << endl; return 0; }
T2
若现在有n个游戏
定义sg函数:能转移到的状态中sg函数里没有出现的最小的自然数
sg[0]=0

sg定理:
n个游戏的sg值=每个sg值异或起来
T3
若现在一次只能取走1-4个石子
同样的操作:sg[0]=0 sg[1]=1 sg[2]=2 sg[3]=3 sg[4]=4 sg[5]=0
T4
n+1堆石子,最左边一堆石头有2012个,两个人分别进行操作。一次操作可以选取两堆不同的石堆分别增加或减少一个石子(一加一减,或给已经不剩石子的堆加一个都是允许的)。为了保证游戏会在有限步内结束,规定所选的两堆中右边的那一堆一定要包含奇数个石子,无路可走者输.问先手是否必胜?
计算n堆的奇偶性,把所有奇数石子堆的下标取出来异或,看答案是否为0
有两堆一样的石子与没有事一个概念
通过转化奇数堆的石子,来解决问题
将最左边一堆视为第0堆,将石子数为奇数的石子堆的编号异或起来,结果为0则先手必败,否则必胜
其实是转化为了nim博弈
T5
u 有N堆石子放在N级楼梯上,楼梯编号为0..N-1,每堆有a[n]个石子。两人轮流游戏,每次将任意堆中的任意个石子移动到它下面那一层楼梯上,0号的石子不能动。直到所有石子都移动到0号,那个人就赢了。问先手是否有必胜策略 。
将距离终点步数为奇数的格子棋子数量异或起来就是答案
T6
u1xN(1<=N<=2000)的空格子,双方轮流操作,每次选一个没有被标记的格子,将其标记,如果某人操作完后,存在3个连续的格子都被标记了,那么他就获胜了,问先手是否有必胜策略?
把一个游戏看成多个游戏
再分成多个游戏
sg[i],对于一个长度为i的横条的sg值为多少
防止越界:在数组后面加一个足够大的数就行
#include<iostream> #include<algorithm> #include<vector> using namespace std; int dfs(int n) { if (n==0) return 0; if (f[n]) return sg[n]; f[n]=true; vector<int> z; for (int a=1;a<=n;a++) { int l = max(a-3,0); int r = max(n-a-2,0); z.push_back( dfs(l) ^ dfs(r) ); } sort(z.begin(),z.end()); z.push_back(233333333); for (int a=0,p=0;;a++) { if (z[p] != a) { sg[n] = a; return sg[n]; } while (z[p]==a) p++; } } int main() { cin >> n; if (dfs(n)) cout << "Alice" << endl; else cout << "Bob" << endl; }
留一个练习:
bzoj2798
Day 7 钟皓曦
消防局的设立
不用dp的做法
N<=100000
f[i][0/1][k]
在自己,父亲,兄弟,爷爷结点都能将其覆盖
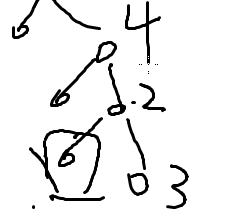
(显然放4结点最优)
首先对于这棵树,找出深度最深的结点,找到其爷爷,在爷爷结点放一个士兵,把他爷爷能覆盖到的结点删掉,以此类推,对剩下的树进行类似操作,直至树全被覆盖
用堆维护,时间复杂度O(n log n)

求出n的k个因子
再计算m^k即可
若将人进行编号,求不同分组呢?
每组有 n/r 个人,则方案数为
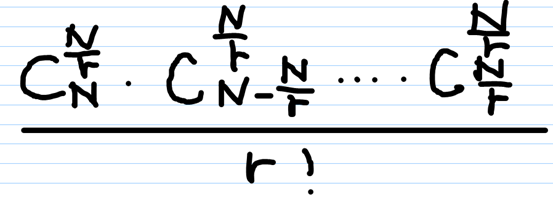
这么多种情况,然后化简
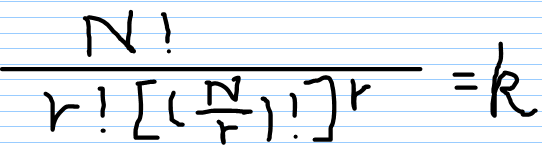

用过欧拉定理后转化为计算
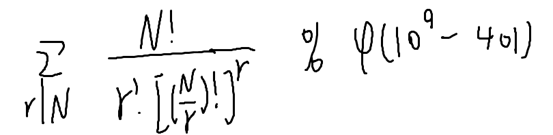

1e9-401是个质数,而1e9-402=2*13*5281*7283
让n的阶乘%2 13 5281 7283
再合并
因为%数较小,一定会有循环节出现





f[i][j]表示走了i步,走到了j

N个点的数,有点权
有m次询问,每次给两个点p1,p2,在这条路径上能否找出三个点,使得它们可以形成三角形
m,n<=1e6
斐波那契数列
若两点的距离大于42,输出yes
若小于等于,暴力即可
bzoj 树上三角形


