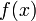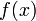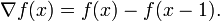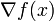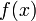图像处理中的一些基本问题解释
作者：gnuhpc
出处：http://www.cnblogs.com/gnuhpc/
差分
，又名差分函数
或差分运算
，是数学中的一个概念。它将原函数
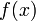映射
到
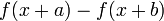。差分运算，相应于微分运算，是微积分
中重要的一个概念。差分的定义分为前向差分
和逆向差分
两种。
则称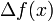
为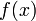
的一阶前向差分。在微积分学中的有限差分
（finite differences），前向差分通常是微分
在离散
的函数中的等效运算。差分方程
的解法也与微分方程
的解法相似。当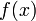
是多项式
时，前向差分为Delta算子，一种线性算子
。前向差分会将多项式阶数降低1。
索贝尔算子 （Sobel operator）是图像处理 中的算子之一，主要用作边缘检测 。在技术上，它是一离散性差分 算子，用来运算图像亮度函数的梯度之近似值。在图像的任何一点使用此算子，将会产生对应的梯度矢量或是其法矢量。
该算子包含两组3x3的矩阵，分别为横向及纵向，将之与图像作平面卷积
，即可分别得出横向及纵向的亮度差分近似值。如果以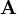
代表原始图像，
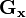及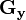
分别代表经横向及纵向边缘检测的图像，其公式如下:
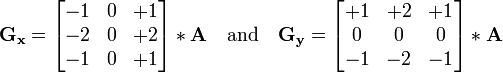
图像的每一个像素的横向及纵向梯度近似值可用以下的公式结合，来计算梯度的大小。
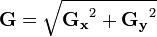
然后可用以下公式计算梯度方向。
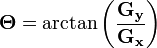
在以上例子中，如果以上的角度Θ 等于零，即代表图像该处拥有纵向边缘，左方较右方暗。
4.矩阵卷积
函数矩阵的卷积
定义两个函数矩阵的卷积可以用类似于两个矩阵乘法的运算规则，即将两个元素相乘的符号都用卷积来替换，譬如
5.图像梯度
感性认识：梯度值就是图像灰度值的显著变化的地方。不同的算子对应了不同的求梯度的方法：
以Sobel算子（效果较好）为例：
对于数字图像，可以用一阶差分代替一阶微分；
△xf(x,y)=f(x,y)-f(x-1,y);
△yf(x,y)=f(x,y)-f(x,y-1)
求梯度时对于平方和运算及开方运算，可以用两个分量的绝对值之和表示，即：
G[f(x,y)]={[△xf(x,y)] +[△yf(x,y)] } |△xf(x,y)|+|△yf(x,y)|;
Sobel梯度算子是先做成加权平均，再微分，然后求梯度，即：
△xf(x,y)= f(x-1,y+1) + 2f(x,y+1) + f(x+1,y+1)- f(x-1,y-1) - 2f(x,y-1) - f(x+1,y-1);
△yf(x,y)= f(x-1,y-1) + 2f(x-1,y) + f(x-1,y+1)- f(x+1,y-1) - 2f(x+1,y) - f(x+1,y+1);
G[f(x,y)]=|△xf(x,y)|+|△yf(x,y)|;
6.高斯金字塔
对于大小为w×i 的图像I，高斯金字塔Gj 由I的几个分辨率减小的高斯图像Ii(i是下标,下同) 组成，其中，i={0,1,...,j}代表金字塔的级数. 图像Ii 的大小为(w/2i)×(h/2i).[2i表示2的i次方]。
图像Ii 是通过对图像Ii-1(i-1是下标) 进行隔行隔列采样而得到的图。
