34排序算法之堆排序

排序算法之堆排序

 

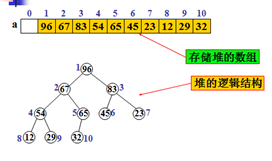
堆的定义：堆是每个非叶结点值都大于或等于其儿子值（父大于子）的完全二叉树。

 

用数组a[n+1]存储长度为n的堆（a[0]不用）

   a[i]≥a[2*i]

   a[i]≥a[2*i+1]

根结点a[1]存储的是最大值（大根堆）-----可以自定义小根堆

 

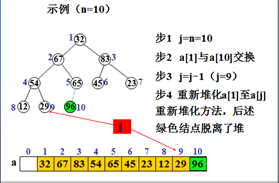
示例

 

 

排序阶段的操作方法：

步骤1）令j=n;j是堆的最大下标，即堆的当前尾指针

步骤2）将a[1]与a[j]交换，将最大元换到当前尾

步骤3）j=j-1；使堆的范围缩小

步骤4）重新堆化（是关键步骤）即调整a[1]至a[j]，使之成为一个新堆

步骤5）若j>1，则转步骤2；否则排序结束

 

 

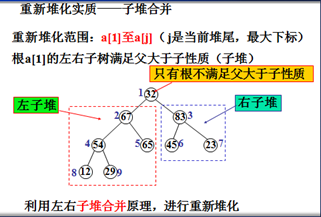
重新堆化的原理：

开始时，每个叶结点单独构成子堆，从最下层的非叶结点起，反复进行子堆合并，自底向上的逐步合并越来越大的堆。

 

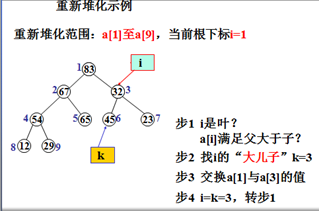
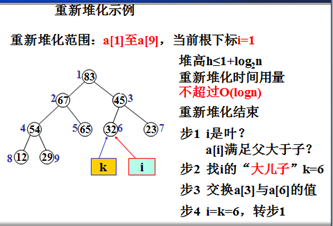
重新堆化步骤：

步骤1）i=1

步骤2）若i是叶，或a[i]已满足父大于子的性质，重新堆化结束；否则继续下一步

步骤3）找i的“大儿子”k

步骤4）交换a[i]与a[k]的值，使根元素下沉

步骤5）i=k，转步骤2

 

 

 

 

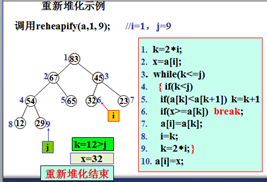
重新堆化函数：

void heapify(int a[],int i, int j)

  { int k,x;

1、2.    k=2i;      x=a[i];

3.    while(k<=j)  // 当i不是叶

        {

4.       if(k<j)  //若i有两个儿子时

5.         if(a[k]<a[k+1])  k=k+1;  //k指向i的大儿子

6.       if(x>=a[k])  break; // i的儿子都不大于a[i]下渗结束

7.       a[i]=a[k], i=k, k=2i;  //大儿子上升, i指向下一

        }

8.   a[i]=x;  //原根元素值就位

     }

 

 

 

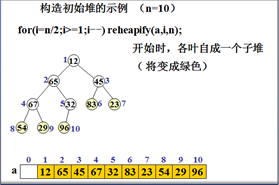
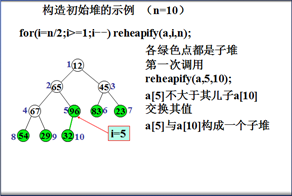
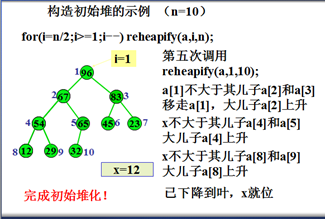
初始堆化示例

例如，输入数据

       12  65  45  67  32  83  23  54  29  96  

 

 

 

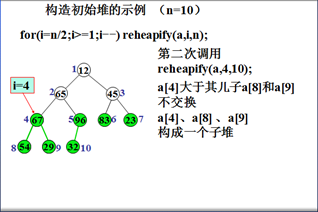
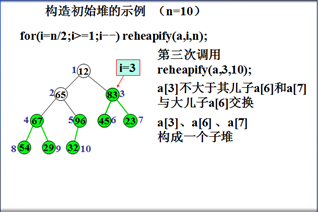
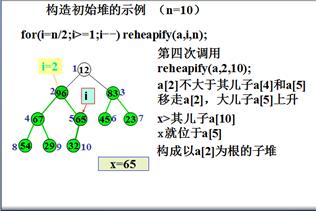
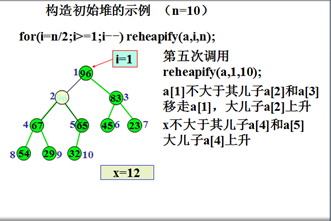
堆排序算法

 

（1）重新堆化函数

void heapify(int a[ ],int i, int j)

   { int k,x;

       函数体见前面

    }

 

（2）重新堆化函数

void heapify(int a[],int i, int j)

  { int k,x;

1、2.    k=2i;      x=a[i];

3.    while(k<=j)  // 当i不是叶

        {

4.       if(k<j)  //若i有两个儿子时

5.         if(a[k]<a[k+1])  k=k+1;  //k指向i的大儿子

6.       if(x>=a[k])  break; // i的儿子都不大于a[i]下渗结束

7.       a[i]=a[k], i=k, k=2i;  //大儿子上升, i指向下一

        }

8.   a[i]=x;  //原根元素值就位

     }

 

（2）主控函数

void heap_sort(int a[ ],int n)

     {     int i,x;

9.    for(i=n/2;i>=1;i- -) heapify(a,i,n);  //初始堆化

10.    for(i=n;i>1;i- -)

11.       {    x=a[1];  a[1]=a[i];  a[i]=x; 

12.            heapify(a,1,i-1);  //重新堆化

           }

      }

 

 

堆排序的源代码：
//调整为大根树
void HeapAdjust(int H[],int begin,int end)
{
    int temp=H[begin];
    int i;
    for(i=2*begin+1;i<=end;i*=2)
    {
        if(i<end-1&&H[i]<H[i+1])    //比较左右子树
            ++i;        //记录较大子树
        if(temp>H[i])    //根节点大于左右子树最大元素的值
            break;
        H[begin]=H[i];
        begin=i;
    }
    H[begin]=temp;        //插入最开始不合标准的元素
}
//堆排序
void HeapSort(int data[],int n/*数组大小*/)
{//建立大根树
    int i;
    for(i=n/2;i>=0;--i)//n/2找到最后一个非叶子节点
        HeapAdjust(data,i,n-1);//真正的调整
    //进行排序
    for(i=n-1;i>0;--i)    //第一个元素与最后一个进行交换
    {
        int temp=data[i];
        data[i]=data[0];
        data[0]=temp;
        //交换后成非大根树，重新调整
        HeapAdjust(data,0,i-1);
    }
}

int main()
{
    int arr[10]={3,5,8,2,4,13,9,1,16,7};
    HeapSort(arr,10)
    for(int i=0;i<10;++i)
        printf("%d ",arr[i]);
    getchar();
    return 0;
}