Kruskal 最小生成树算法

对于一个给定的连通的无向图 G = (V, E)，希望找到一个无回路的子集 T，T 是 E 的子集，它连接了所有的顶点，且其权值之和为最小。

因为 T 无回路且连接所有的顶点，所以它必然是一棵树，称为生成树（Spanning Tree），因为它生成了图 G。显然，由于树 T 连接了所有的顶点，所以树 T 有 V - 1 条边。一张图 G 可以有很多棵生成树，而把确定权值最小的树 T 的问题称为最小生成树问题（Minimum Spanning Tree）。术语 "最小生成树" 实际上是 "最小权值生成树" 的缩写。

Kruskal 算法提供一种在 O(ElogV) 运行时间确定最小生成树的方案。Kruskal 算法基于贪心算法（Greedy Algorithm）的思想进行设计，其选择的贪心策略就是，每次都选择权重最小的但未形成环路的边加入到生成树中。其算法结构如下：

1. 将所有的边按照权重非递减排序；
2. 选择最小权重的边，判断是否其在当前的生成树中形成了一个环路。如果环路没有形成，则将该边加入树中，否则放弃。
3. 重复步骤 2，直到有 V - 1 条边在生成树中。

上述步骤 2 中使用了 Union-Find 算法来判断是否存在环路。

例如，下面是一个无向连通图 G。

图 G 中包含 9 个顶点和 14 条边，所以期待的最小生成树应包含 (9 - 1) = 8 条边。

首先对所有的边按照权重的非递减顺序排序：

Weight Src Dest
1 7 6
2 8 2
2 6 5
4 0 1
4 2 5
6 8 6
7 2 3
7 7 8
8 0 7
8 1 2
9 3 4
10 5 4
11 1 7
14 3 5

然后从排序后的列表中选择权重最小的边。

1. 选择边 {7, 6}，无环路形成，包含在生成树中。

2. 选择边 {8, 2}，无环路形成，包含在生成树中。

3. 选择边 {6, 5}，无环路形成，包含在生成树中。

4. 选择边 {0, 1}，无环路形成，包含在生成树中。

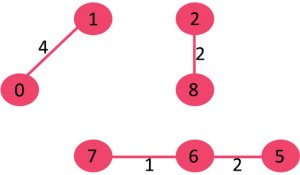
5. 选择边 {2, 5}，无环路形成，包含在生成树中。

6. 选择边 {8, 6}，有环路形成，放弃。

7. 选择边 {2, 3}，无环路形成，包含在生成树中。

8. 选择边 {7, 8}，有环路形成，放弃。

9. 选择边 {0, 7}，无环路形成，包含在生成树中。

10. 选择边 {1, 2}，有环路形成，放弃。

11. 选择边 {3, 4}，无环路形成，包含在生成树中。

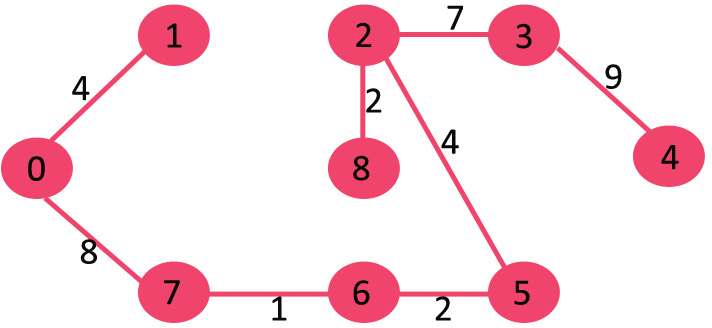
12. 由于当前生成树中已经包含 V - 1 条边，算法结束。

C# 实现的 Kruskal 算法如下。

using System;
using System.Collections.Generic;
using System.Linq;

namespace GraphAlgorithmTesting
{
  class Program
  {
    static void Main(string[] args)
    {
      Graph g = new Graph(9);
      g.AddEdge(0, 1, 4);
      g.AddEdge(0, 7, 8);
      g.AddEdge(1, 2, 8);
      g.AddEdge(1, 7, 11);
      g.AddEdge(2, 3, 7);
      g.AddEdge(2, 5, 4);
      g.AddEdge(8, 2, 2);
      g.AddEdge(3, 4, 9);
      g.AddEdge(3, 5, 14);
      g.AddEdge(5, 4, 10);
      g.AddEdge(6, 5, 2);
      g.AddEdge(8, 6, 6);
      g.AddEdge(7, 6, 1);
      g.AddEdge(7, 8, 7);

      Console.WriteLine();
      Console.WriteLine("Graph Vertex Count : {0}", g.VertexCount);
      Console.WriteLine("Graph Edge Count : {0}", g.EdgeCount);
      Console.WriteLine();

      Console.WriteLine("Is there cycle in graph: {0}", g.HasCycle());
      Console.WriteLine();

      Edge[] mst = g.Kruskal();
      Console.WriteLine("MST Edges:");
      foreach (var edge in mst)
      {
        Console.WriteLine("\t{0}", edge);
      }

      Console.ReadKey();
    }

    class Edge
    {
      public Edge(int begin, int end, int weight)
      {
        this.Begin = begin;
        this.End = end;
        this.Weight = weight;
      }

      public int Begin { get; private set; }
      public int End { get; private set; }
      public int Weight { get; private set; }

      public override string ToString()
      {
        return string.Format(
          "Begin[{0}], End[{1}], Weight[{2}]",
          Begin, End, Weight);
      }
    }

    class Subset
    {
      public int Parent { get; set; }
      public int Rank { get; set; }
    }

    class Graph
    {
      private Dictionary<int, List<Edge>> _adjacentEdges
        = new Dictionary<int, List<Edge>>();

      public Graph(int vertexCount)
      {
        this.VertexCount = vertexCount;
      }

      public int VertexCount { get; private set; }

      public IEnumerable<int> Vertices { get { return _adjacentEdges.Keys; } }

      public IEnumerable<Edge> Edges
      {
        get { return _adjacentEdges.Values.SelectMany(e => e); }
      }

      public int EdgeCount { get { return this.Edges.Count(); } }

      public void AddEdge(int begin, int end, int weight)
      {
        if (!_adjacentEdges.ContainsKey(begin))
        {
          var edges = new List<Edge>();
          _adjacentEdges.Add(begin, edges);
        }

        _adjacentEdges[begin].Add(new Edge(begin, end, weight));
      }

      private int Find(Subset[] subsets, int i)
      {
        // find root and make root as parent of i (path compression)
        if (subsets[i].Parent != i)
          subsets[i].Parent = Find(subsets, subsets[i].Parent);

        return subsets[i].Parent;
      }

      private void Union(Subset[] subsets, int x, int y)
      {
        int xroot = Find(subsets, x);
        int yroot = Find(subsets, y);

        // Attach smaller rank tree under root of high rank tree
        // (Union by Rank)
        if (subsets[xroot].Rank < subsets[yroot].Rank)
          subsets[xroot].Parent = yroot;
        else if (subsets[xroot].Rank > subsets[yroot].Rank)
          subsets[yroot].Parent = xroot;

        // If ranks are same, then make one as root and increment
        // its rank by one
        else
        {
          subsets[yroot].Parent = xroot;
          subsets[xroot].Rank++;
        }
      }

      public bool HasCycle()
      {
        Subset[] subsets = new Subset[VertexCount];
        for (int i = 0; i < subsets.Length; i++)
        {
          subsets[i] = new Subset();
          subsets[i].Parent = i;
          subsets[i].Rank = 0;
        }

        // Iterate through all edges of graph, find subset of both
        // vertices of every edge, if both subsets are same, 
        // then there is cycle in graph.
        foreach (var edge in this.Edges)
        {
          int x = Find(subsets, edge.Begin);
          int y = Find(subsets, edge.End);

          if (x == y)
          {
            return true;
          }

          Union(subsets, x, y);
        }

        return false;
      }

      public Edge[] Kruskal()
      {
        // This will store the resultant MST
        Edge[] mst = new Edge[VertexCount - 1];

        // Step 1: Sort all the edges in non-decreasing order of their weight
        // If we are not allowed to change the given graph, we can create a copy of
        // array of edges
        var sortedEdges = this.Edges.OrderBy(t => t.Weight);
        var enumerator = sortedEdges.GetEnumerator();

        // Allocate memory for creating V ssubsets
        // Create V subsets with single elements
        Subset[] subsets = new Subset[VertexCount];
        for (int i = 0; i < subsets.Length; i++)
        {
          subsets[i] = new Subset();
          subsets[i].Parent = i;
          subsets[i].Rank = 0;
        }

        // Number of edges to be taken is equal to V-1
        int e = 0;
        while (e < VertexCount - 1)
        {
          // Step 2: Pick the smallest edge. And increment the index
          // for next iteration
          Edge nextEdge;
          if (enumerator.MoveNext())
          {
            nextEdge = enumerator.Current;

            int x = Find(subsets, nextEdge.Begin);
            int y = Find(subsets, nextEdge.End);

            // If including this edge does't cause cycle, include it
            // in result and increment the index of result for next edge
            if (x != y)
            {
              mst[e++] = nextEdge;
              Union(subsets, x, y);
            }
            else
            {
              // Else discard the nextEdge
            }
          }
        }

        return mst;
      }
    }
  }
}

输出结果如下：

参考资料

• Connectivity in a directed graph
• Strongly Connected Components
• Tarjan's Algorithm to find Strongly Connected Components

本篇文章《Kruskal 最小生成树算法》由 Dennis Gao 发表自博客园，未经作者本人同意禁止任何形式的转载，任何自动或人为的爬虫转载行为均为耍流氓。